7.6余角与补角[上学期]

课件22张PPT。7.4　　余角和补角乌牛中学 谢理福合作学习 图7-33图7-32概念 如果两个锐角的和是一个直角，我们就说这两个角互为余角，简称互余，也可以说其中一个角是另一个角的余角。 如果两个角的和是一个平角，我们就说这两个角互为补角，简称互补，也可以说其中一个角是另一个角的补角。180o做一做∵ ∠ １＋ ∠ ３＝ ４２°＋ ４８°＝９０ °，
∴ ∠ １与 ∠ ３互余.
∵ ∠ １＋ ∠ ２＝ ４２°＋ １３８°＝１８０ °，
∴ ∠ １与 ∠ ２互补.∵ ∠ＢＯＤ＋ ∠ＤＯＣ＝ ∠ＢＯＣ＝ ∠ＡＯＣ＝Ｒt ∠
∴ ∠ＢＯＤ与 ∠ＤＯＣ互余．
∵ ∠ＡＯＣ＋∠ＢＯＣ＝１８０　∠ＡＯＤ＋∠ＢＯＤ＝１８０ °，
∴ ∠ＡＯＣ与∠ＢＯＣ互补， ∠ＡＯＤ＋∠ＢＯＤ互补．?????×断真伪×看谁思考的快！！
　　1．锐角的余角一定是锐角吗？
　　2．一个锐角和一个钝角一定互为补角吗？
　　3．一个角的补角比这个角的余角大多少度？
　　4．相等且互补的两个角各是多少度？
　　5．一个角的补角一定比这个角大吗？一定（不一定）（大90°）（90°、 90°）（不一定）比一比，谁完成的最好1、若∠1与∠2互余， ∠1+∠2= °，若∠1与∠2互补，则∠1+∠2=　　 ° 2、30°角的余角为 　 °，补角为　 °，75°30′的余角为 ，补角为 。 n°(0 ＜ n＜90)的余角为 ，补角为 。901806015014°30′104°30′90°-n°180°-n°∠COD∠BOD∠AOD10°
55°
75°
100°
145°
35°
80°
105°
125°
170°10°
15°
35°
55°
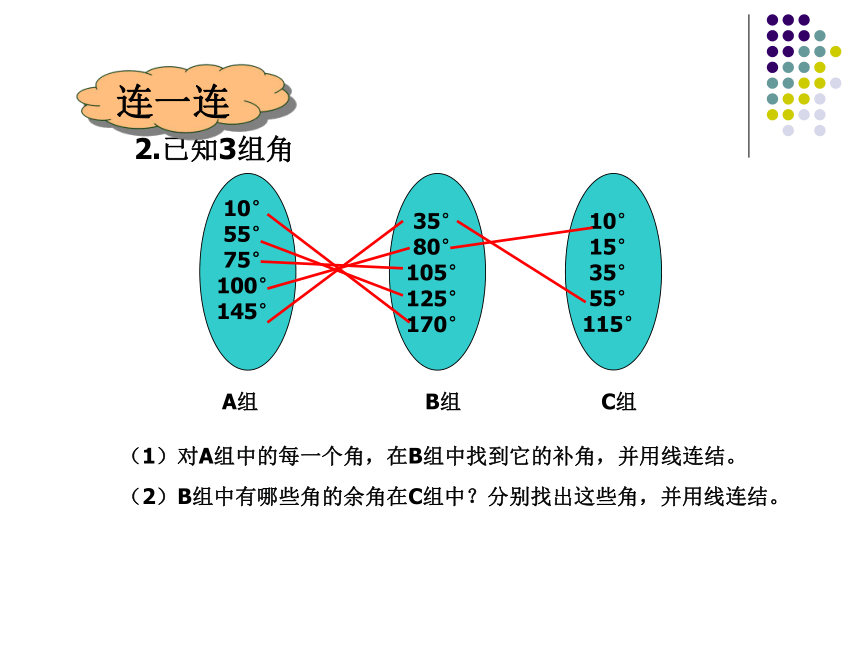
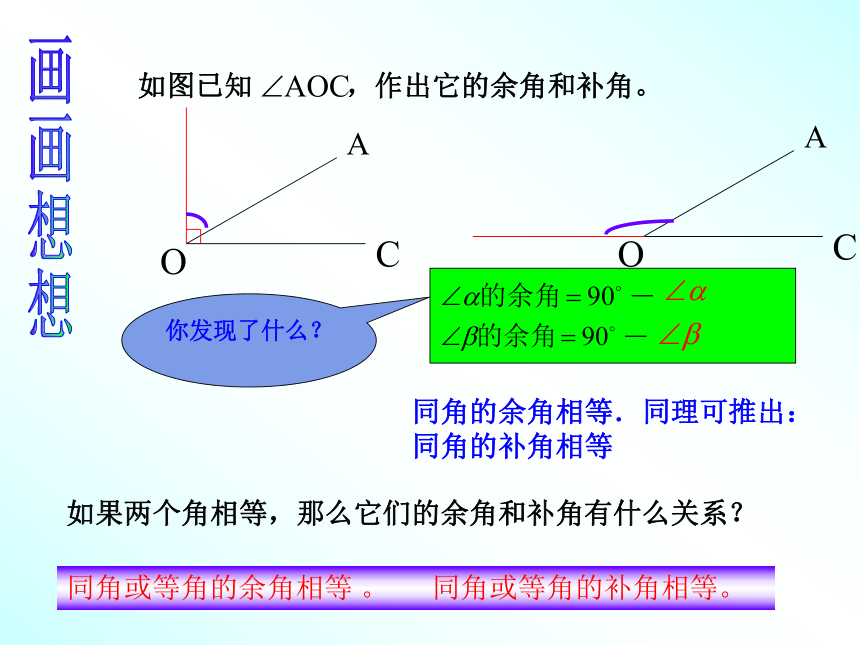
115°2.已知3组角A组B组C组（1）对A组中的每一个角，在B组中找到它的补角，并用线连结。（2）B组中有哪些角的余角在C组中？分别找出这些角，并用线连结。连一连画画想想你发现了什么？同角的余角相等．同理可推出：同角的补角相等如果两个角相等，那么它们的余角和补角有什么关系？同角或等角的余角相等 。 同角或等角的补角相等。练一练如图：∠A+∠B=90°,∠BCD+∠B=90°,∠A与∠BCD有什么大小关系？为什么？BCAD答：∠A=∠BCD因为∠A+∠B=90° ∠BCD+∠B=90°所以∠A=∠BCD（同角的余角相等）
所以∠A=90°- ∠B ∠BCD=90°-∠B例１　　如右图，已知∠ ＡＯＣ＝ ∠ＢＯＤ＝Ｒt ∠．指出图中还有哪些角相等，并说明理由． 解：∠ ＡＯＢ＝ ∠ＣＯＤ理由：　　∵ ∠ ＡＯＣ＝ ∠ＢＯＤ＝Ｒt ∠，
　　∴ ∠ ＡＯＢ＋ ∠ ＢＯＣ＝Ｒt ∠，
　　　∠ ＣＯＤ＋ ∠ ＢＯＣ＝Ｒt ∠，
即　　∠ ＡＯＢ与∠ ＣＯＤ都是∠ ＢＯＣ的余角，
　　∴ ∠ ＡＯＢ＝ ∠ＣＯＤ　（　　　　　　　　）
同角的余角相等想一想： ∠1与∠2互补，∠3与∠4互补，若∠1=∠3，那么∠2和∠4相等吗？为什么？由此你有能得出什么结论？
因为∠1与∠2互补，∠3与∠4互补答：∠2和∠4相等又因为∠1=∠3结论：同角（或等角）的补角相等所以∠2=∠4所以∠2=180°-∠1，∠4=180°- ∠3
练一练如图，直线CD经过点O，且OC平分∠AOB。试判断∠AOD与∠BOD的大小关系，并说明理由。ODABC答：∠AOD=∠BOD因为∠AOD与∠AOC互补，∠BOD与∠BOC互补所以∠AOD=180°- ∠AOC
∠BOD=180°-∠BOC又因为OC平分∠AOB
所以∠AOD=∠BOD（等角的补角相等）所以∠AOC=∠BOC1、如图1，∠AOB=∠COD=Rt∠，请找出另外相等的角，并说明理由。图1根据互余互补你会填吗？180°60°150°29°28′119°28′90－X，180－X150°例 2 已知一个角的补角是这个角的余角的4倍,求这个角的度数.解: 设这个角为 x 度,则这个角的余角是 (90 – x) 度,补角是 ( 180 – x ) 度.由题意,得 180 – x = 4 ( 90 – x ),解方程,得 x=60 (度)所以这个角的度数为60 °做一做一个角的补角减去20°后，等于这个角的余角的2倍，求这个角的度数。课内练习:已知 ∠а=60°32’, ∠а的余角是多少度? ∠а的补角是多少度?
2. 如图,吊桥与铅垂方向所成的角∠а=30°.若要把吊桥放平,则吊桥需沿什么方向转动?转动多少度的角?
(1)如果∠а的余角是∠а的2倍,求∠а的度数;
(2)如果∠1的补角是∠1的三倍,求∠1的度数.
CDENAOBM?1＋ ?2＝90°?1＋ ?2＝180°同角(等角)的余角相等同角(等角)的补角相等课堂小结下图中，OA是表示南偏西30o方向上的一条射线，仿照这条射线，画出表示下列方向的射线：（1）北偏西20o；（2）南偏东60o； （3）西南方向（即南偏西45o）。30o20o60o45o表示（1）、（2）方向的两条射线所成的角是多少度？表示（2）、（3）方向的两条射线所成的角呢？在日常生活中，我们什么时候会用到这样的表示法？140o105o表示目标方位思考在一幅学校的地图上，有教学楼、食堂、图书馆三地，但被墨迹污染，图书馆的具体位置看不清，只知道图书馆在教学楼的东北方向，在食堂的南偏西60o方向，你能确定图书馆的位置吗？图书馆45o60o作业：
作业题和作业本。再见