实数[上学期]

课件13张PPT。3.2 实数复习回顾　　想一想，昨天上课学习到了哪些知识，并试着将下面的填空题补充完整：　１、一个正数　有　　　个平方根，正平方根用　　　表示，负平方根用　　　表示．零的平方根等于　　　，　　　没有平方根．两零负数　２、正数的　　　平方根和　　　的平方根，统称算术平方根．一个数　　　　的算术平方根记作　　　．　　　正零有理数整数分数　　每一个有理数都可以在数轴上表示出来．
例如－２，－０.５，　和３都可以在数轴上
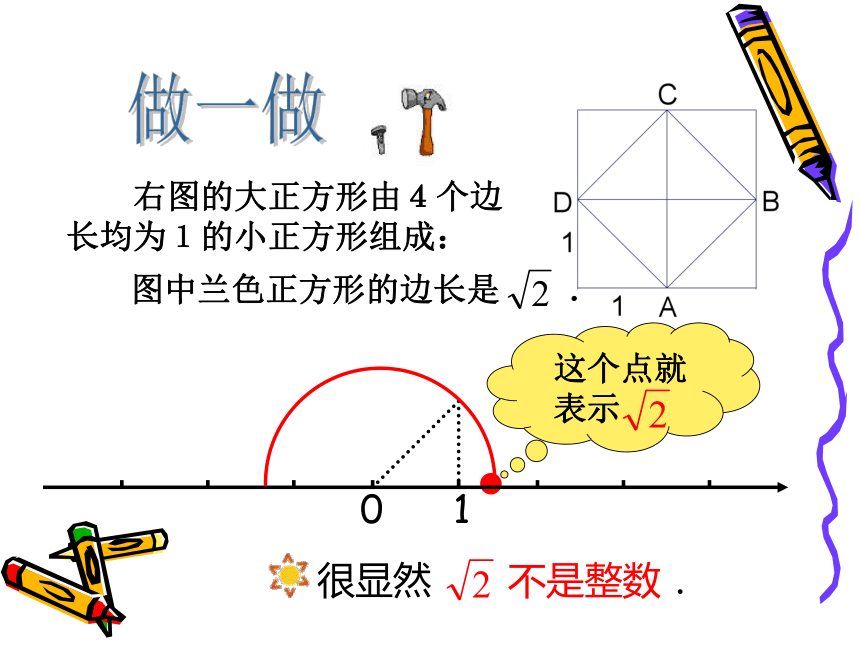
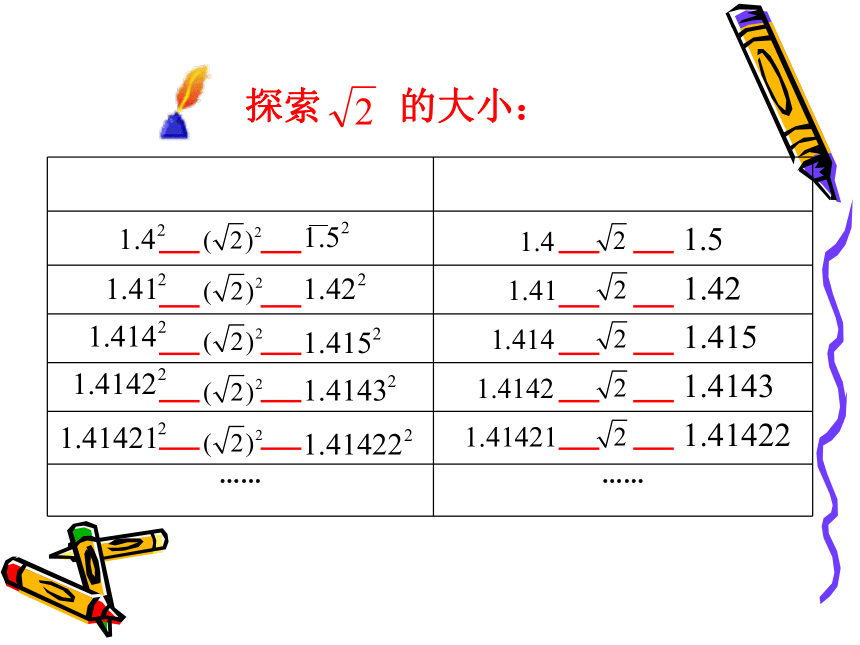
表示出来．　　思考：数轴上的每一个点都表示一个有理数吗？做一做　　右图的大正方形由４个边长均为１的小正方形组成：图中兰色正方形的边长是　　．很显然　　不是整数．这个点就表示 探索　　的大小：　　　既不是有限小数，也不是无限循环小数，因此，　不是分数．　　　不是有理数，它是一个无限不循环小数．像 这种无限不循环小数叫做无理数。例如：正有理数负有理数零负无理数正无理数有理数无理数实 数有理数和无理数统称为实数（real number）．， ， ， ， ， ， ， ，练习1：把下列各数分别填入表示数的集合的横线上： （每两个1之间依次多一个2） 属于有理数的有：
属于正无理数的有：
属于负无理数的有：
属于实数的有：练习2：（1） 的相反数是 ；（2） ； （3）一个数的绝对值是 ，则这个数
是　　　． 在实数范围内，每一个数都可以用数轴上的点来表示；反过来，数轴上的每一点都表示一个实数．我们说实数和数轴上的点一一对应． 在数轴上表示的两个实数，右边的数总比左边的数大。 练习3：把下列实数表示在数轴上，并比较它们的大小（用“＜”号连接）：， ， ， ， ， 练习4．下列说法正确吗？请说明理由。
（1）无理数是无限小数； （ ）
（2）有理数是有限小数； （ ）
（3）无限小数是无理数； （ ）
（4）有理数都是实数，实数都是有理数； （ ）
（5）无理数是带根号的数； （ ）
（6）带根号的数都是无理数； （ ）