7.3比较线段的长短（2）[上学期]

课件19张PPT。7.3 线段的长短比较（2）（1）重(叠)合法—从“形”的角度比较
（2）度量法—从“数值”的角度比较1.比较线段
长短的方法2、用直尺和圆规作一条线段，使它等于已知线段、两条已知线段的和差。
3、若线段c的长度是线段a,b的长度的和(差)，我们就说线段c是线段a,b的和(差)
回顾思考： 合 作 学 习请按下面的步骤操作：
1、在一张透明纸上画一条线段AB；
2、对折这张纸，使线段AB的两个
端点重合；
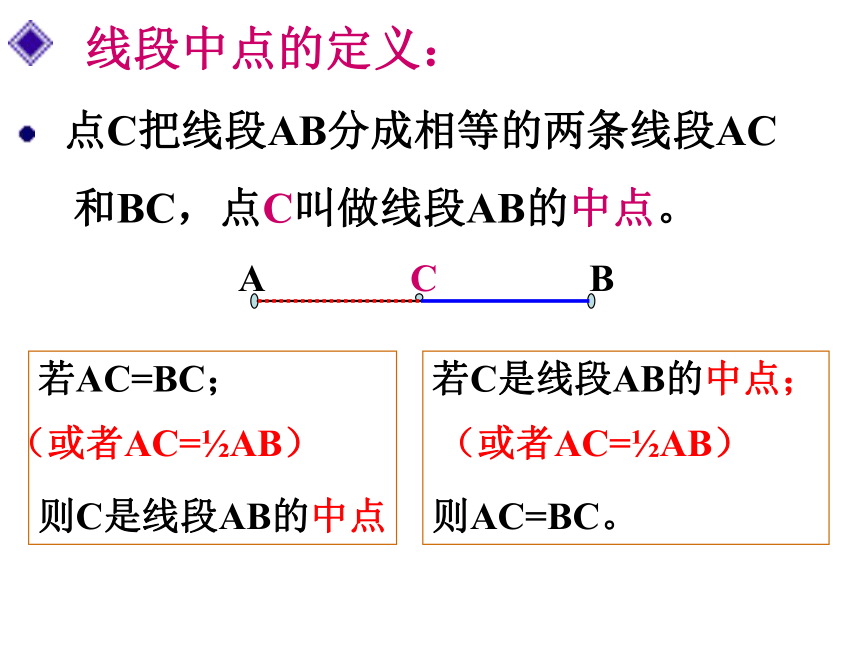
3、把纸展开铺平，标明折痕点C。问：线段AC和线段BC相等吗？ 线段中点的定义： 点C把线段AB分成相等的两条线段AC
和BC，点C叫做线段AB的中点。ABC若AC=BC；
则C是线段AB的中点若C是线段AB的中点；
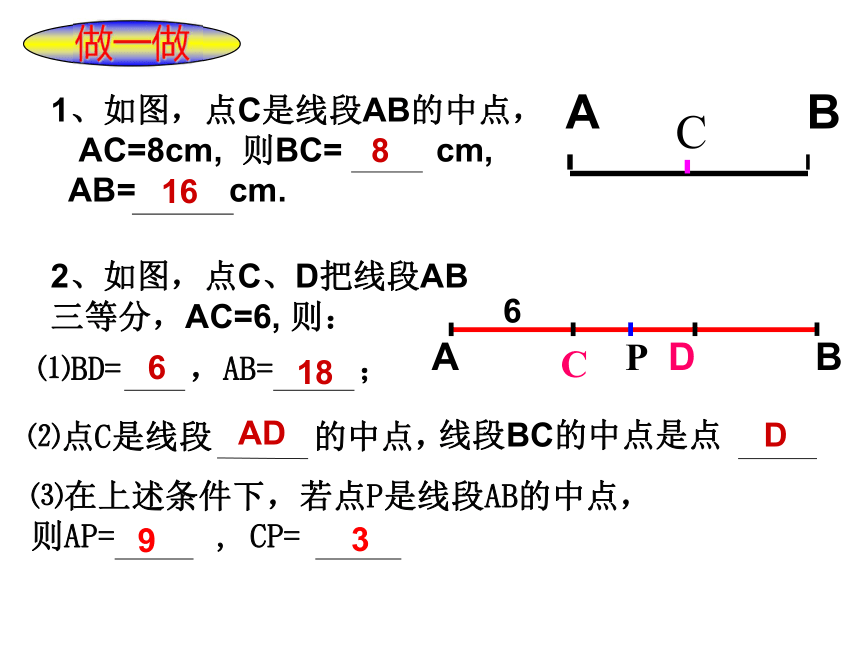
则AC=BC。（或者AC=?AB）（或者AC=?AB）做一做1、如图，点C是线段AB的中点，
AC=8cm, 则BC= cm,
AB= cm.C2、如图，点C、D把线段AB
三等分，AC=6, 则：⑴BD= ，AB= ；⑵点C是线段　　　的中点，
　线段BC的中点是点　　　　。816618ADD⑶在上述条件下，若点P是线段AB的中点，
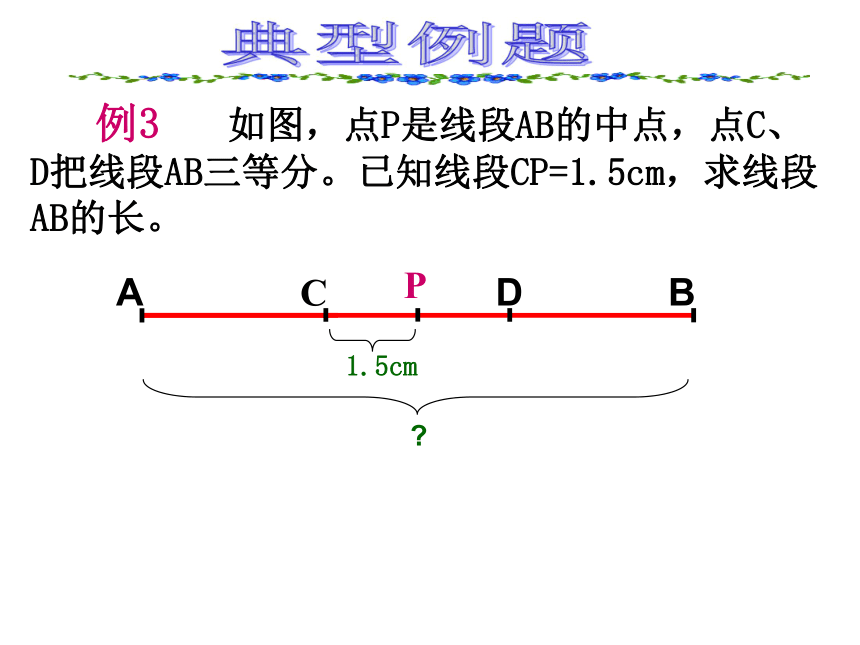
则AP= , CP=93 例3 如图，点P是线段AB的中点，点C、D把线段AB三等分。已知线段CP=1.5cm，求线段AB的长。典型例题1. 任意画一条线段AB,用刻度尺量出它的
长，然后找出它的中点C,并写出AC,BC
的长。课内练习p172： 已知B是线段AC上一点,AB=4cm,BC=3cm. 如果O是线段AC的中点, 求线段OB的长。 补 充 练 习（1）如图 AB=6cm，点C是AB的中点，
点D是CB的中点，则AD=____cm（2）如图，下列说法 ，不能判断点C是线段AB的中点的是( )
A、AC=CB B、AB=2AC
C、AC+CB=AB D、CB= AB C4.5猫为什么总是沿着
笔直的路线扑向老鼠？学校1路2路3路4路 小明为了
尽快到学校，应选择第 ＿＿条路。为什么？
小明家 线段的性质： 在我们生活中有多少利用这条性质的例子? 如图，从小明家到学校共有4条路，4 在所有连结两点的线中，
线段最短。
（两点之间线段最短）大家看图，如果量一量新城车站与麻行码头相距多远，是怎样量的？如果从你家到学校走了三公里，能否认为学校与你家的距离为3公里？两点之间线段的长度， 叫做这两点之间的距离。麻行码头新城车站（2）如图：这是A、B两地之间的公路，
在公路工程改造计划时，为使A、B两地
行程最短，应如何设计线路？在图中画出。
你的理由是
_______________________________练一练:长度两点之间线段最短（1）两点之间的距离是指
两点之间的线段 的 ( ) 问题征答下列说法正确的是(　　)
过A、B两点的直线长是A、B两点间的距离
B.线段AB就是A、B两点间的距离
C.乘火车从杭州到上海要走210千米，这就是说
　杭州站与上海站间的距离为210千米
D. 连结A、B两点的所有线中，其中最短的线的长度
　就是A、B两点间的距离D村庄A村庄B大桥P河流如图，村庄A, B之间有一条河流，要在河
流上建造一座大桥P, 为了使村庄A, B之间
的距离最短，请问：这座大桥P应建造在
哪里。为什么？请画出图形。两点之间线段最短 线段的基本性质： AP如图，立方体纸盒P处粘有一粒
糖，A处有一只蚂蚁沿着纸
盒表面爬向糖粒。你能帮助
蚂蚁找到一条最短的路线吗？
请在图上画出这条最短路线，
并说明理由。PA两点之间线段最短 线段的基本性质： 课堂小结：这节课你学会了什么？2.线段的基本性质：两点之间线段最短。3.两点之间的距离：两点之间线段的长度。1.线段的中点的概念及表示方法。直线的基本性质：两点确定一条直线作业友情提示
（1）作业本(1)第37页
（2）课本第173页作业题1---5
（3）预习：P173---177页再 见