5.3.3一元一次方程的应用(3)[上学期]
文档属性
| 名称 | 5.3.3一元一次方程的应用(3)[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2005-11-21 18:47:00 | ||
图片预览






文档简介
课件19张PPT。
一元一次方程的应用(3)
基 础 练 习1、甲每天生产某种零件80个,3天能生产 个零件。
2、乙每天生产某种零件x个,5天能生产 个零件。
3、甲每天生产某种零件80个,乙每天生产某种零件x个。
他们5天一共生产 个零件。
4、甲每天生产某种零件80个,乙每天生产这种零件x个
甲生产3天后,乙也加入生产同一种零件,再经过5天,
两人共生产 个零件。
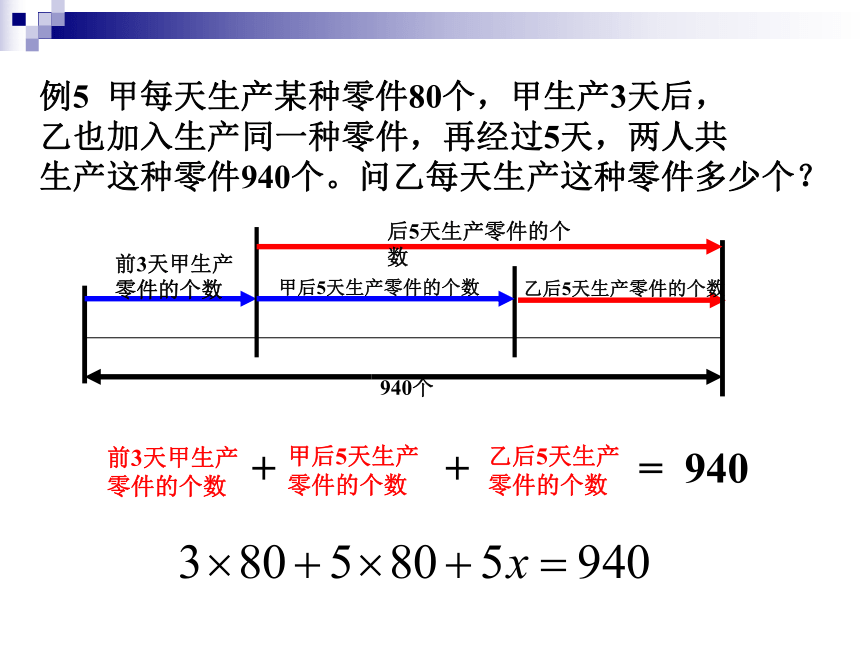
工程问题的基本数量关系:工作总量=工作时间×工作效率3×805x(5×80+5x)(3×80+5×80+5x)例5 甲每天生产某种零件80个,甲生产3天后,
乙也加入生产同一种零件,再经过5天,两人共
生产这种零件940个。问乙每天生产这种零件多少个?0.97624X基 础 练 习
1、小明把5000元按一年期的定期储蓄存入银行,年 利率为1.98%,到期后可得利息 元。
2、小明把x元按一年期的定期储蓄存入银行,年利
率为1.98%,到期后可得利息 元。
3、小明把x元按一年期的定期储蓄存入银行,年利率为1.98%,利息税的税率为20%,到期后应交利息
税 元。
最后小明实得本利和为 元。5000× 1.98%1.98%x1.98%x×20%0.00396x(X+0.0198x–0.00396x)例6 小明把压岁钱按定期一年存入银行。当时一年期定期
存款的年利率为1.98%,利息税的税率为20%。到期支取
时扣除利息税后小明实得本利和为507.92元。问小明存入
银行的压岁钱有多少元?1、本金×利率=利息2、利息×税率=利息税3、本金 +利息–利息税=实得本利和
这里有哪些等量关系?解:设:小明存入银行的压岁钱有x元,由题意得
解得:x=500检验:x=500适合方程,且符合题意.
答:小明存入银行的压岁钱有500元.
利润:指商品售价与进价之间的差额,即:
利润=售价-进价
一:基本概念成本价(进价或本金):商家取得某一商品所需要的
付出的金额。标价:商家出售商品时所标明的价格。售价:指商品成交时的实际价格;利润率:指利润与成本的比率,即:
利润率 =
1. 一件商品的销售价为100元,买入价为90元,
则毛利润为 元。
2. 某商品的原价是x元,若按七五折出售,
售价是 。
3. 一件夹克成本价为50元,提价50%后标价,
再按标价的8折出售,则售价为 元。
打折销售10600.75x4、 某服装店以每件a元的成本价购入服装,按成
本价提高30%后标价,则
(1)若按标价出售,每件售价是 元,每件
获利 元。
(2)若按标价的9折(即90%)出售,则每件售价
元,获利 元。
(3)若按标价9折出售,每件获利17元,依题意可
列方程得 ,解此方程 。1.3a0.3a1.17a0.17a0.17a=17a=1001.某种风扇因季节原因准备打折出售,如果按定价的7.5折出售,将赔30元;如果按定价的9折出售,将赚25元,问这种风扇的原定价为多少元? 同类变式 某商品的进价是2000元,标价是3000元,若商店要求以利润率不低于5%的售价打折出售,则售货员最低可以打几折出售此商品?x等量关系是什么?x 2、王老师带领团员若干人到赤壁游览,现联系了两辆车的车主。甲车主给出的优惠条件是:学生9折,老师不收费;乙车主给出的优惠条件是:包括老师在内,全部按8折优惠。如果每张车票的价格是40元,那么乘哪家车主的车比较合算?解:设有X个学生,由题意得甲车主:乙车主:课内练习: 1.某装潢公司接到一项业务,如果由甲组做需10天完成,由乙组做需15天完成。为了早日完工,现由甲、乙两组一起做,4天后甲组因另有任务,余下部分由乙组单独做,问还需几天才能完成?解:设乙组还需x天才能完成解得:x=5检验:x=5适合方程,且符合题意.
答:还需5天才能完成.2.某年二年期定期储蓄的年利率为2.25%,所得利息需交纳20%的利息税,已知某储户到期后实得利息450元。问该储户存入本金多少元?解:设储户存入本金x元,由题意得检验x=12500适合方程,且符合题意.
答:该储户存入本金12500元.作业题:1、老王把5000元按一年期的定期储蓄存入银行,
到期支取时,扣去利息税后实得本利和为5080元。
已知利息税税率为20%,问当时一年期定期储蓄
的年利率为多少?解:设一年期定期储蓄的年利率为x,由题意得解得:x=2%检验:x=2%适合方程,且符合题意.
答:当时一年期定期储蓄
的年利率为2%
2、一件商品按成本价提高30%后标价,又以8折
销售,售价为208元,这种商品的成本价是多少元?解:设成本价为x元,由题意得检验:x=200适合方程,且符合题意.
答:这种商品的成本价是200元.3.一收割 机队每天收割小麦12公顷,收割完一片麦地的 后,该收割机改进操作,效率提高到原来的 倍,因此比预定时间提早1天完成.问这片麦地 有多少公顷?解:设这片麦地 有X公顷,由题意得检验:x=180适合方程,且符合题意.
答:这片麦地 有180公顷4.列举一个实际情境应用题,要求能用方程
(1—25%)X=112.5求解。5、某商店有两种不同型号的计算器的出售价都是64元,
卖出其中一种计算器商店盈利为进货价的60%,卖出另
一种商店亏损进货价的20%。若卖出这两种计算器1台,
这家商店的盈亏情况如何?
解:设甲种计算器进货价为X元,由题意得64—X=60%X
解得:X=40设乙种计算器进货价为y元,由题意得64—y=—20%y
解得:y=80答:商店盈利8元. 墙上钉着用一根彩绳围成的梯形形状的饰物,如图中的实线所示。小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图中的虚线所示,小颖所钉的长方形的长、宽各是多少厘米?请你做一做41024442课 堂 小 结1、工程问题的基本数量关系:
工作总量=工作时间×工作效率2、利率的基本关系:
本金×利率=利息
利息×税率=利息税
本金 +利息–利息税=实得本利和
3、运用方程解决实际问题的一般过程:审题设元列方程解方程检验
一元一次方程的应用(3)
基 础 练 习1、甲每天生产某种零件80个,3天能生产 个零件。
2、乙每天生产某种零件x个,5天能生产 个零件。
3、甲每天生产某种零件80个,乙每天生产某种零件x个。
他们5天一共生产 个零件。
4、甲每天生产某种零件80个,乙每天生产这种零件x个
甲生产3天后,乙也加入生产同一种零件,再经过5天,
两人共生产 个零件。
工程问题的基本数量关系:工作总量=工作时间×工作效率3×805x(5×80+5x)(3×80+5×80+5x)例5 甲每天生产某种零件80个,甲生产3天后,
乙也加入生产同一种零件,再经过5天,两人共
生产这种零件940个。问乙每天生产这种零件多少个?0.97624X基 础 练 习
1、小明把5000元按一年期的定期储蓄存入银行,年 利率为1.98%,到期后可得利息 元。
2、小明把x元按一年期的定期储蓄存入银行,年利
率为1.98%,到期后可得利息 元。
3、小明把x元按一年期的定期储蓄存入银行,年利率为1.98%,利息税的税率为20%,到期后应交利息
税 元。
最后小明实得本利和为 元。5000× 1.98%1.98%x1.98%x×20%0.00396x(X+0.0198x–0.00396x)例6 小明把压岁钱按定期一年存入银行。当时一年期定期
存款的年利率为1.98%,利息税的税率为20%。到期支取
时扣除利息税后小明实得本利和为507.92元。问小明存入
银行的压岁钱有多少元?1、本金×利率=利息2、利息×税率=利息税3、本金 +利息–利息税=实得本利和
这里有哪些等量关系?解:设:小明存入银行的压岁钱有x元,由题意得
解得:x=500检验:x=500适合方程,且符合题意.
答:小明存入银行的压岁钱有500元.
利润:指商品售价与进价之间的差额,即:
利润=售价-进价
一:基本概念成本价(进价或本金):商家取得某一商品所需要的
付出的金额。标价:商家出售商品时所标明的价格。售价:指商品成交时的实际价格;利润率:指利润与成本的比率,即:
利润率 =
1. 一件商品的销售价为100元,买入价为90元,
则毛利润为 元。
2. 某商品的原价是x元,若按七五折出售,
售价是 。
3. 一件夹克成本价为50元,提价50%后标价,
再按标价的8折出售,则售价为 元。
打折销售10600.75x4、 某服装店以每件a元的成本价购入服装,按成
本价提高30%后标价,则
(1)若按标价出售,每件售价是 元,每件
获利 元。
(2)若按标价的9折(即90%)出售,则每件售价
元,获利 元。
(3)若按标价9折出售,每件获利17元,依题意可
列方程得 ,解此方程 。1.3a0.3a1.17a0.17a0.17a=17a=1001.某种风扇因季节原因准备打折出售,如果按定价的7.5折出售,将赔30元;如果按定价的9折出售,将赚25元,问这种风扇的原定价为多少元? 同类变式 某商品的进价是2000元,标价是3000元,若商店要求以利润率不低于5%的售价打折出售,则售货员最低可以打几折出售此商品?x等量关系是什么?x 2、王老师带领团员若干人到赤壁游览,现联系了两辆车的车主。甲车主给出的优惠条件是:学生9折,老师不收费;乙车主给出的优惠条件是:包括老师在内,全部按8折优惠。如果每张车票的价格是40元,那么乘哪家车主的车比较合算?解:设有X个学生,由题意得甲车主:乙车主:课内练习: 1.某装潢公司接到一项业务,如果由甲组做需10天完成,由乙组做需15天完成。为了早日完工,现由甲、乙两组一起做,4天后甲组因另有任务,余下部分由乙组单独做,问还需几天才能完成?解:设乙组还需x天才能完成解得:x=5检验:x=5适合方程,且符合题意.
答:还需5天才能完成.2.某年二年期定期储蓄的年利率为2.25%,所得利息需交纳20%的利息税,已知某储户到期后实得利息450元。问该储户存入本金多少元?解:设储户存入本金x元,由题意得检验x=12500适合方程,且符合题意.
答:该储户存入本金12500元.作业题:1、老王把5000元按一年期的定期储蓄存入银行,
到期支取时,扣去利息税后实得本利和为5080元。
已知利息税税率为20%,问当时一年期定期储蓄
的年利率为多少?解:设一年期定期储蓄的年利率为x,由题意得解得:x=2%检验:x=2%适合方程,且符合题意.
答:当时一年期定期储蓄
的年利率为2%
2、一件商品按成本价提高30%后标价,又以8折
销售,售价为208元,这种商品的成本价是多少元?解:设成本价为x元,由题意得检验:x=200适合方程,且符合题意.
答:这种商品的成本价是200元.3.一收割 机队每天收割小麦12公顷,收割完一片麦地的 后,该收割机改进操作,效率提高到原来的 倍,因此比预定时间提早1天完成.问这片麦地 有多少公顷?解:设这片麦地 有X公顷,由题意得检验:x=180适合方程,且符合题意.
答:这片麦地 有180公顷4.列举一个实际情境应用题,要求能用方程
(1—25%)X=112.5求解。5、某商店有两种不同型号的计算器的出售价都是64元,
卖出其中一种计算器商店盈利为进货价的60%,卖出另
一种商店亏损进货价的20%。若卖出这两种计算器1台,
这家商店的盈亏情况如何?
解:设甲种计算器进货价为X元,由题意得64—X=60%X
解得:X=40设乙种计算器进货价为y元,由题意得64—y=—20%y
解得:y=80答:商店盈利8元. 墙上钉着用一根彩绳围成的梯形形状的饰物,如图中的实线所示。小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图中的虚线所示,小颖所钉的长方形的长、宽各是多少厘米?请你做一做41024442课 堂 小 结1、工程问题的基本数量关系:
工作总量=工作时间×工作效率2、利率的基本关系:
本金×利率=利息
利息×税率=利息税
本金 +利息–利息税=实得本利和
3、运用方程解决实际问题的一般过程:审题设元列方程解方程检验
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
