3.2实数[上学期]

课件26张PPT。成功的花
人们只惊慕她现在的明艳
然而她当初的芽儿
却洒遍牺牲的血雨
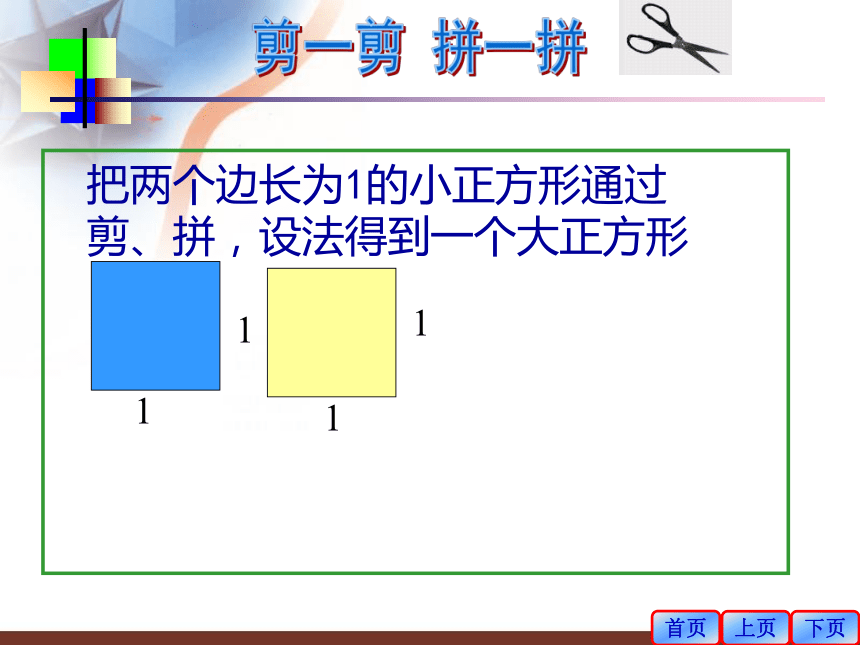
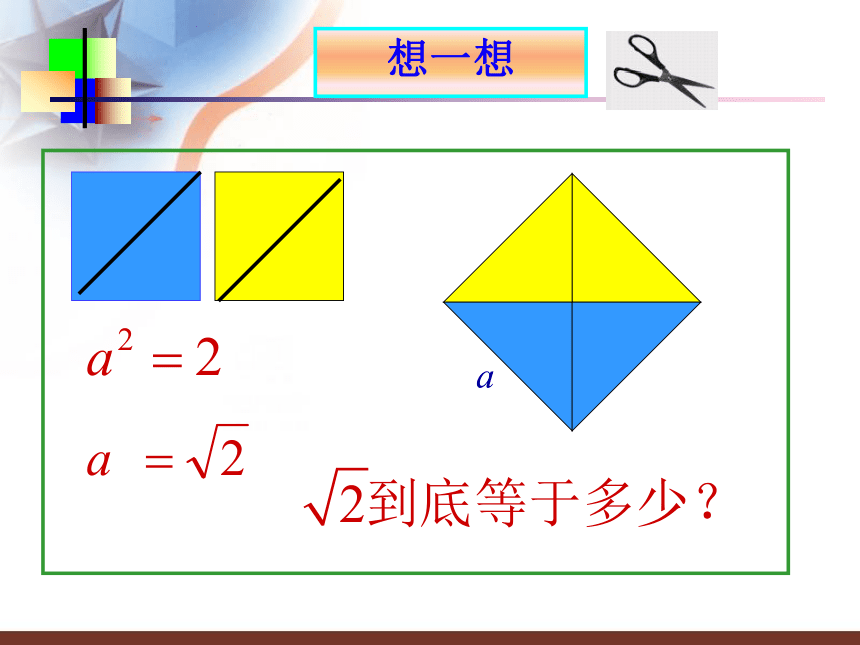
浸透了奋斗的泪泉——冰心3.2实数制作:徐育育首页上页下页把两个边长为1的小正方形通过剪、拼，设法得到一个大正方形剪一剪 拼一拼1111想一想概念引入 它是一个
有理数吗？=1.41421356237309504880168872420969807856967187537694807317667973799073247846210703885038……答:它既不是有限小数,也不是无限不循环小数,也就是说 不是有理数.无理数概念学习首页上页下页像 这种无限不循环小数叫做无理数,无理数广泛存在着,例如:例如：圆周率 及一些含有 的数都是无理数有一定的规律，但不循环的无限小数都是无理数。例如：0.1010010001…
〔两个1之间依次多1个0〕
-168.3232232223…
〔两个3之间依次多1个2〕0.12345678910111213 …
〔小数部分有相继的正整数组成〕
无理数也像有理数一样广泛存在着。


无理数也有正负之分，例如知识回顾请回忆:有理数的分类有理数按定义分：按符号分：实数有理数正有理数负有理数零无理数正无理数负无理数有理数和无理数统称为实数。或 有理数整数分数（无限不循环小数）实数的定义及其分类练习1首页上页下页完成课本73页课内练习1.注意:把数从有理数扩充到实数以后,有理数的相反数和绝对值的概念任然适用于实数.完成课本72页”做一做”.如何把无理数在数轴上表示出来?首页上页下页实数和数轴上的点一一对应把下列无理数表示在数轴上,并比较它们的大小:( 用“<”连接)的表示的表示无理数的小故事公元前580～568年之间的古希腊,
数学家毕达哥拉斯建立了毕达哥拉斯学派?
该学派的成员希伯索斯根据勾股定理
（西方称为毕达哥拉斯定理）通过逻辑
推理发现，边长为1的正方形的对角线长
度既不是整数，也不是整数的比所能表示。
希伯索斯的发现被认为是“荒谬”和违反常识的事?它不仅严重地违背了毕达哥拉斯
学派的信条，也冲击了当时希腊人的传统见解。
使当时希腊数学家们深感不安，
相传希伯索斯因这一发现被投入海中淹死，
这就是第一次数学危机.欣赏有趣的图形：其中正方形ABCD的边长是1cm，你能找到一条长度不是有理数的线段吗？神奇的π
我们已经知道，π是一个无理数。在日常应用中，大多数人只须知道π的前四位小数值就够了，然而数学家对π的研究却经历了许多世纪。当代数学大师、著名的美籍华裔数学家陈省身教授感慨道：“π这个数渗透了整个数学！”有的数学家甚至说：“历史上一个国家所算得的圆周率的准确程度，可以作为衡量这个国家当时数学发展的一面旗帜。”
祖冲之
(南北朝) 刘徽
（魏晋时期） 阿基米德
（古希腊） ??刘徽（约公元3世纪）首创了一种割圆术的数学方法，算出π的近似值为3.1416，计算圆周率精确到了小数点后第3位（后人称之为徽率）。割圆术的数学思想，用刘徽的原话讲就是：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”实际上，割圆术已孕育了微积分的思想。
祖冲之（公元429—500年）是继刘徽之后的一位杰出的数学家，他把刘徽创造的割圆术成果又向前推进了一步，计算圆周率精确到小数点后第七位，即3.1415926<π <3.1415927 还得到π的两个近似值：约率22/7 和密率355/113 。密率是一个很好的近似分数值，它是分子分母在1000以内最接近π值的分数． 1593年，也就是1000多年后，才被德国数学家鄂图（otto）重新得到。1655年英国数学家wallis将π表示为无穷乘积的形式：
π=2×
1609年，德国数学家ludolph把π的近似值算到了小数点后35位，几乎耗尽了一生的时间。为了纪念他，人们给他的墓碑上刻上他算得的π值：3.141 592 653 589 793 238 462 643 383 279 502 881674年，德国数学家leibniz证明了
π=π=4×(1－ + － + － + － +…)
1706年英国数学家machin利用公式π=16arctg1/5-4arctg1/239（其中arctgx=
计算到了100位的圆周率 。因为它的计算过程中被乘数和被除数都不大于长整数，所以可以很容易地在计算机上编程实现。 1597年，法国数学家viete得公式：
　　
特别值得一提的是，当代著名的数论专家Atle Selberg(1917-)曾经说，他喜欢数学的一个动机，是以下公式：
　　
　　大家看，这个公式多美呀
17世纪，瑞士数学家euler给出的公式1873年，英国数学家shanks出版了一本估值的书，他把的值求到了小数点后707位，由于当时没有计算机，他是用手工算的，足足算了20年。然而到1946年，有科学家提出shanks给出的第528位以后是错的。至2002年底，科学家们用超级计算机已把 π 的值算到小数点后12411亿位.
那么为什么数学家们还象登山运动员那样，奋力向上攀登，一直求下去而不是停止对 π 的探索呢？为什么其小数值有如此的魅力呢？这其中大概免不了有人类的好奇心与领先于人的心态作怪，但除此之外，还有许多其它原因。　1它与概率等其他数学领域的研究有着密切的联系。2它可以检验超级计算机的硬件和软件的性能。3计算π的方法和思路可以引发新的概念和思想。