不等式的性质2[上学期]

课件21张PPT。不等式和它的基本性质不等式和它的基本性质引导性材料：
1.如课本P54图，能看出物体A的重量比多少
克重？比多少克轻？
2.据气象预报，某天的最高气温是10℃，最
低气温为-5℃，由此我们说这一天的气温
不低于 ℃，并且不高于 ℃；
3.统计全班同学的年龄，年龄最大者为16岁，
可以知道全班每个同学的年龄都 17岁； 若设物体A的重量为x克；某天的气温为t℃；
本班某同学的年龄为a岁，上述不等关系能用式子
表示出来吗？-510小于不等式和它的基本性质 x＞2，x ＜3，t≥-5，t≤10 ，a ＜17
-7＜-5，3+4＞1+4，5+3≠12-5
a+2＞a+1，x+3 ＜6 ，a≠0，
(1)上述式子有哪些表示数量关系的符号？
这些符号表示什么关系？
(2)这些符号两侧的代数式可随意交换
位置吗？
(3)什么叫不等式？（表示不等关系）（不可随意互换位置）（用不等号表示不等关系的式子叫不等式）不等式和它的基本性质练习：
1.判断下列式子哪些是不等式？为什么？
(1)3＞ 2 (2)a2+1＞ 0 (3)3x2+2x
(4)x＜ 2x+1 (5)x=2x-5
(6)x2+4x＜ 3x+1 (7)a+b≠c2.用“＞”或“＜”填空：
(1)4 -6 (2)-1 0 (3)-8 -3 (4)-4.5 -4
(5)7+3 4+3 (6)7+(-3) 4+(-3)
(7)7×3 4×3 (8)7×(-3) 4×(-3)√√√√√＞＞＞＞＜＜＜＜不等式和它的基本性质3.用不等式表示：
(1)a是正数
(2)a是负数
(3)x与3的和小于6
(4)x与2的差大于-1
(5)x的4倍大于等于7
(6)y的一半小于3a＞0a＜0x+3＜6x-2＞-14x≥7y＜3不等式和它的基本性质解: (1) a＜0 ;
(2)a≥0;
(3) 6x-3＞10 ;例1.用不等式表示：
(1) a是负数；(2) a是非负数；
(3) x的6倍减去3大于10；
(4)y的 与6的差小于1;
(5)y的 与6的差不小于1. y-6＜1.
(5) y-6≥1不等式和它的基本性质 1.你能检验x=2及x=3是否为方程x+3=6
的解吗？ 2.已知数值：-5, 0.5, 3, 0, 2, -2.5, 5.2
(1)判断:上述数值，哪些使不等式x+3＜6
成立？哪些使之不成立？
(2)说出几个使不等式x+3＜6成立的x的值，
及使之不成立的x的值. 总结：判断不等式是否成立的方法--------
不等号两边的大小关系是否与不等号一致不等式和它的基本性质反馈练习：
1.当x取下列数值时，哪些是不等式
x+3＞6解？
-4, -2.5, 0, 1, 3.5, 4, 4.5, 72. x=2是不是不等式x+3＞4的解？
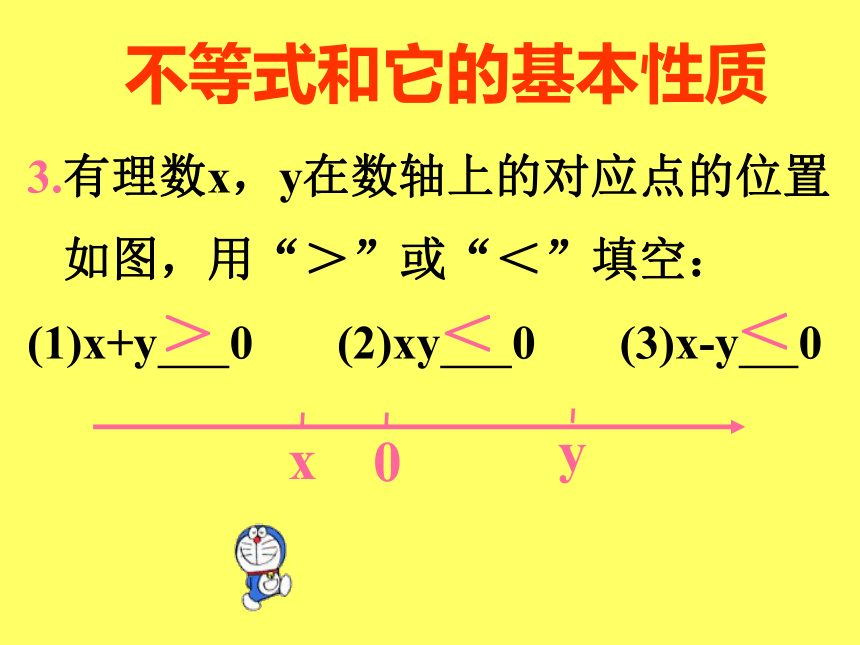
当x=1.5时呢？当x=-1时呢？√√√√不等式和它的基本性质3.有理数x，y在数轴上的对应点的位置
如图，用“＞”或“＜”填空：
(1)x+y 0 (2)xy 0 (3)x-y 0＞＜＜不等式和它的基本性质4.(1)用不等式表示：x与3的和小于等于6；解：(1)x+3≤6；(2)x取-5，0，0.5，2，3时不等式成立；(3)x≤3时，不等式x+3≤6总成立；
x＞3时，不等式x+3≤6总不成立.(2)写出使上述不等式成立的几个x的值；(3)x取何值时，不等式x+3≤6总成立？
取何值时总不成立？不等式和它的基本性质5.绝对值小于3的非负整数有 ；
6.下列选项正确的是（ ）
A. a不是负数，则a＞0
B. b是不大于0的数，则b＜0；
C. m不小于-1，则m＞-1；
D. a+b是负数，则a+b＜０.
7.A市某天的最低气温是-7℃，最高气温
是6℃，设这天气温为t℃，则 t满足的
条件是 .0，1，2D-7≤t≤6不等式和它的基本性质8.依题意列不等式：
（1）a的3倍与7的差是非正数；
（2）x与6的和大于9且小于12.解：（1）3a-7≤0
（2）9＜x+6＜12不等式和它的基本性质小结：
1.掌握不等式是否成立的判断方法；
2.依题意列出正确的不等式.
（注意：表示不等关系的词语要用
不等号来表示，“不大于”即“≤”，
“不小于”即“≥” ）不等式和它的基本性质1.什么是等式？
2.等式的基本性质是什么？
3.用“＞”或“＜”填空：
7 + 3 4 + 3 7 +（-3） 4 +（-3）
7×3 4×3 7×（-3） 4×（-3）
(1)上述不等式中哪题的不等号与7＞4
一致？
(2)观察思考，猜出不等式的基本性质＞＞＞＜不等式和它的基本性质不等式的三条基本性质：
1. 不等式两边都加上（或减去）同一个
数或同一个整式，不等号的方向不变；
2. 不等式两边都乘（或除以）同一个
正数，不等号的方向不变；
3.*不等式两边都乘（或除以）同一个
负数，不等号的方向改变 ；---如何用数学语言表示？
---与等式的基本性质有什么联系与区别？不等式和它的基本性质解：(1)根据不等式基本性质1，两边都
加上2，得 x-2+2＜3+2
x＜5
(2)根据不等式基本性质1，两边都减去5x，
得 6x-5x＜5x-1-5x
x＜-1例1.根据不等式的基本性质，把下列
不等式化成x＜a或x＞a的形式：
(1) x-2＜ 3 (2) 6x＜ 5x-1
(3) x＞5 (4) -4x＞3不等式和它的基本性质例2.设a＞b，用“＜”或“＞”填空：
(1)a-3 b-3 (2) (3) -4a -4b解：(1) ∵a＞b
∴两边都减去3，由不等式基本性质1
得 a-3＞b-3
(2) ∵a＞b，并且2＞0
∴两边都除以2，由不等式基本性质2
得 (3) ∵a＞b，并且-4＜0
∴两边都乘以-4，由不等式基本性质3
得 -4a＜-4b＞不等式和它的基本性质变式训练：
1.用“＞”或“＜”在横线上填空，并在题后
括号内填写理由.
∵a＞b (2)∵ a＞b
∴a-4 b-4( ) ∴ 4a 4b( )
(3)∵3m＞5n (4)∵4x＞5x
∴ -m ( ) ∴ x 0( )
(5)∵ ＜ (6)∵a-1＜8
∴ a 2b( ) ∴ a 9( ) ＞＞＞＜＜＜不等式基
本性质1不等式基
本性质3不等式基
本性质3不等式基
本性质1不等式基
本性质2不等式基
本性质1不等式和它的基本性质2.单项选择：
(1)由 x＞y 得 ax＞ay 的条件是（ ）
A.a＞0 B.a＜0 C.a≥0 D.a≤0
(2)由 x＞y 得 ax≤ay 的条件是（ ）
A.a＞0 B.a＜0 C.a≥0 D.a≤0
(3)由 a＞b 得 am2＞bm2 的条件是（ ）
A.m＞0 B.m＜0 C.m≠0 D.m是任意有理数
(4)若 a＞1，则下列各式中错误的是（ ）
A.4a＞4 B.a+5＞6 C. ＜ D.a-1＜0ADCD不等式和它的基本性质3.判断正误：
(1)∵a+8＞4 (2)∵3＞2
∴a＞-4 ( ) ∴3a＞2a( )
(3)∵-1＞-2 (4)∵ab＞0
∴a-1＞a-2 ( ) ∴a＞0,b＞ 0( )√×√×不等式和它的基本性质归纳小结：
1.本节重点
(1)掌握不等式的三条基本性质，尤其是性质3；
(2)能正确应用性质对不等式进行变形；
2.注意事项
（1）要反复对比不等式性质与等式性质
的异同点；
（2）当不等式两边都乘以（或除以）同
一个数时，一定要看清是正数还是
负数；对于未给定范围的字母，应
分情况讨论.