2.6 探索勾股定理 1[上学期]

课件24张PPT。勾股定理授 课 教 师 常 山 城 关 中 学 王 亚 君主讲内容教材分析教法与学法分析 板书设计 教学过程设计 教 材 分 析教材所处的地位 勾股定理是欧氏几何中最著名的定理之一，是数形结合优美的典范。它有着悠久的历史，在数学与人类的实践活动中有着极其广泛的应用。学生通过对勾股定理的学习，可以在原有的基础上对直角三角形有进一步的认识和理解。
教学目标 知识目标：能说出勾股定理的内容，会初步运用勾股定理进行简单的计算和实际运用。
能力目标：（1）通过对勾股定理的理解和运用，提高学生分析问题和解决问题的能力，开发学生的逻辑思维能力。
（2）通过勾股定理的探索过程，培养学生观察，分析的能力，让学生经历“观察——猜想——归纳——验证”的数学思想，并体会数形结合和特殊到一般的思想方法。
情感目标：激发兴趣，树立信心。通过介绍勾股定理在中国古代的研究，激发学生热爱祖国，热爱祖国悠久文化的思想，激励学生发奋学习。
教学重点 勾股定理及应用。 用面积相等法证明勾股定理。教学难点教学重点与难点教法分析 ：建构教学模式，启发、引导、探索
学法指导 ：自主探索，合作交流
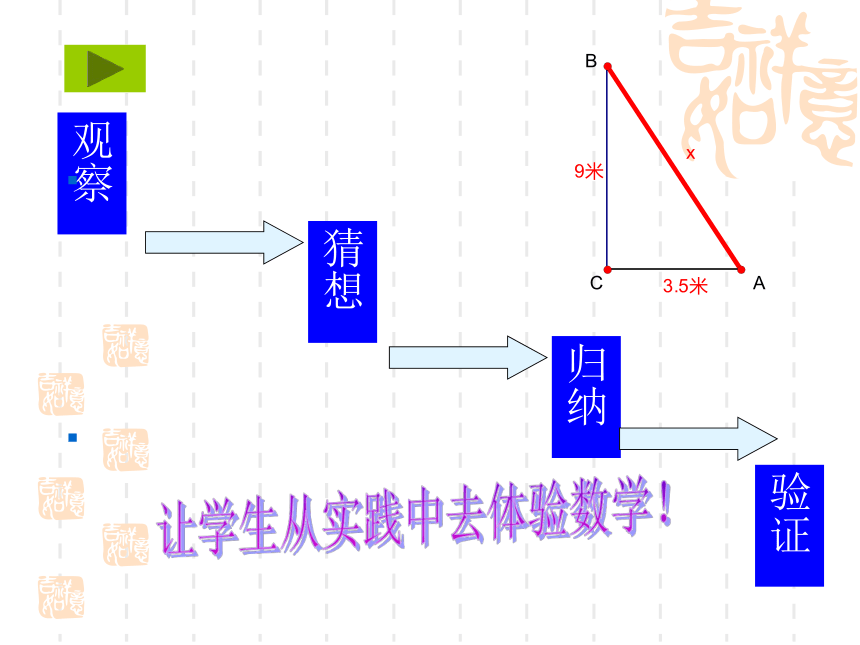
教学手段 ：多媒体， 实物投影教法与学法分析教学过程设计交流对话，探究新知创设情境，引出课题 布置作业，挖掘潜能应用新知，体验成功梳理概括，形成结构小结反思，自主发展生活链接，巩固提高解决问题，前呼后应观察验证归纳让学生从实践中去体验数学！
猜想32+42=52利用直尺测量特殊的直角三角形的三边,如3,4,552+122=132 介绍”勾、股、弦”的定义
用符号语言表示：∠C=Rt∠,AB=c,AC=b,BC=a
a2+b2=c2 猜想： AB2=AC2+BC2
证明猜想 提示：利用面积相等法来证明。 法一： 法二： 定理的证明方法有几百种,连美国第20届总统伽菲尔德于1881年也提供了面积证法。我国古代数学家利用割补。拼接图形来计算。 法三： (a+b)2/2=c2/2+2*ab/2


我国称“勾股定理”，西方称“毕达哥拉斯”定理，为什么呢？
①介绍《周髀算经》中西周的商高（公元一千多年前）发现勾股定理。
②西方毕达哥拉斯于公元前582——493时期发现。
③康熙数学专著《勾股图解》有五种求解直角三角形的方法，其中积求勾股法是独创。
在直角三角形中，两条直角边的平方和等于斜边的平方
△ABC中，若∠C=Rt∠,AB=c,AC=b,BC=a
a2+b2=c2 勾股定理应用新知，体验成功 例一、△ABC中，∠C=Rt∠,BC=a,AC=b,AB=c
①已知a=6,b=8,求c ②已知a=15,c=17,求b 例二、某超市为方便顾客购物要建一传送电梯，已知楼高4米，电梯底部距楼底9米，请问传送电梯的履带需多长
？解决问题，前呼后应 分析：构造直角三角形，看梯子的长度是否大于直角三角形的斜边的长。
解：△ABC中，∠C=Rt∠,BC=a,AC=b,AB=c, a=9,b=3.5
因为a2+b2=92+3.52 = 81+12.25=93.25
所以 c2 =93.25 =93.25
而6.52=42.25<93.25
所以梯子不能进入三楼
梳理概括，形成结构 内容总结：探索直角三角形两直角边的平方和等于斜边的平方，利用勾股定理解决实际问题。
方法归纳：（1）证明勾股定理，利用面积相等的方法
（2）数形结合的方法
（3）把实物抽象成数学模型。生活链接，巩固提高 链接一已知一台29寸电视的底边宽为25寸,则这台电视有多高?
想一想链接二：一艘船在A处要到达小岛B处,但A、B 之间有暗礁，为了行船安全，船先向正西方向行使了400海里，再向正南方向行使了300海里便到达小岛B，
请你计算A与B之间的直线距离是多少？
小结反思，自主发展 引导学生对本课学习反思小结：
我最大的收获
我表现较好的方面
我掌握了怎样的学法
我还有疑惑……
勾股数的求法
如果a是一个大于1的奇数,b,c为两个连续自然数,
且有a2=b+c,则a,b,c为一组勾股数,
如3,4,5是一组勾股数,且有32=4+5
5,12,13是 一组勾股数,52=12+13
7,24,25是一组够勾股数,72=24+25
如果a,b,c是一组勾股数,则na,nb,nc也是一组勾股数,n为自然数
如 3,4,5
6,8,10
9,12,15
布置作业，挖掘潜能 书面作业：必做P571；
选做P572
补充：如图四边形ABCD中，
AB=8，BC=9，CD=12，其中
BC⊥CD，AB⊥BD，求AD

实践探索：请同学们收集日常生活中可用勾 股定理来解决的实际问题（以小组为单位完成）。
板书设计 勾股定理
时间安排 复习引入约三分钟，实验操作约十分钟，归纳验证约七 分钟，例题讲解约十四分钟，巩固练习约七分钟，小结作业约四分钟 。
请多多指导，谢谢！常山县城关中学 执教：王亚君