矩形的性质[下学期]

课件18张PPT。探索矩形的性质
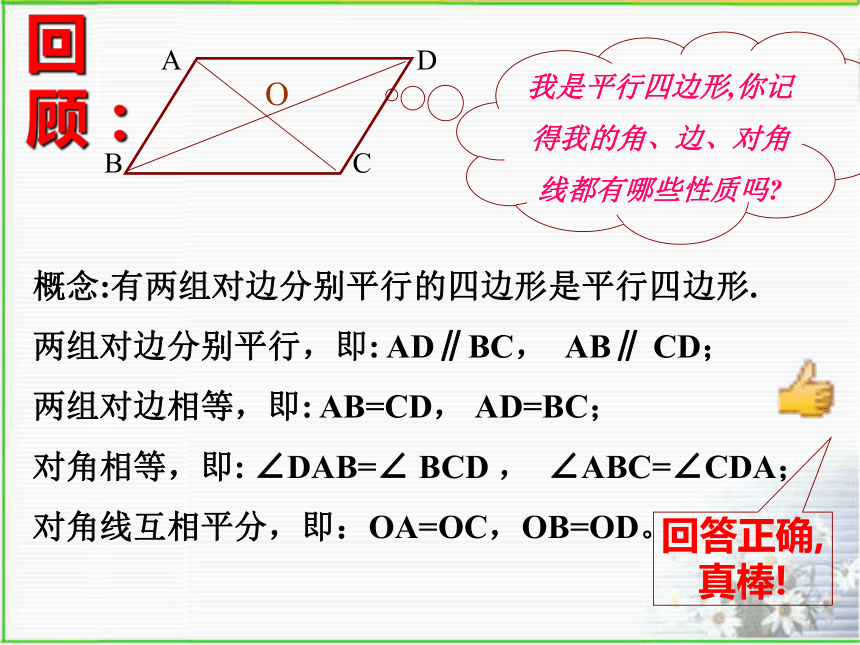
2007.4.13我是平行四边形,你记得我的角、边、对角线都有哪些性质吗?概念:有两组对边分别平行的四边形是平行四边形.
两组对边分别平行，即: AD∥BC， AB∥ CD；
两组对边相等，即: AB=CD， AD=BC；
对角相等，即: ∠DAB=∠ BCD ， ∠ABC=∠CDA；
对角线互相平分，即：OA=OC，OB=OD。回答正确,
真棒!回顾：
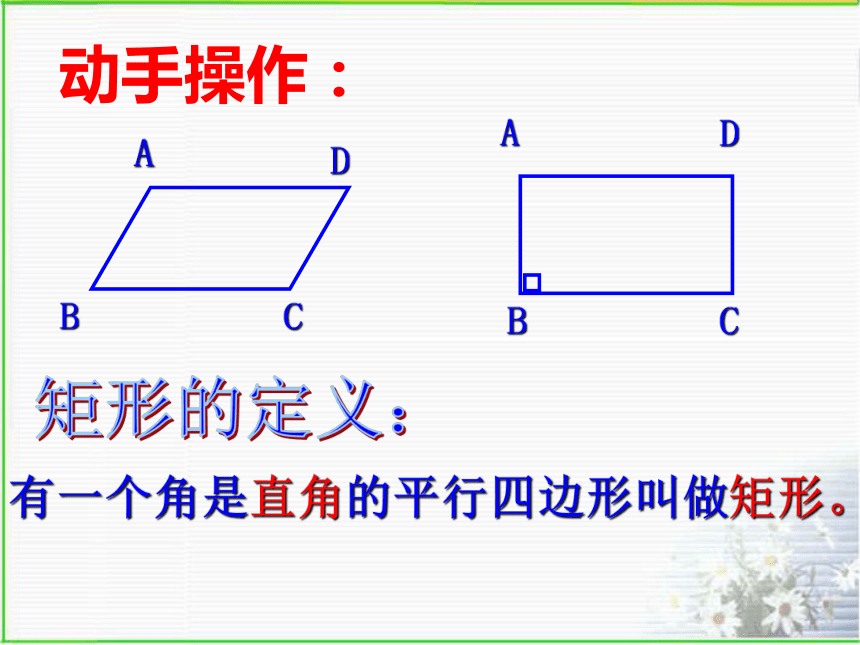
有一个角是直角的平行四边形叫做矩形。 动手操作：矩形的定义：矩形：木门纸张电脑显示器有一个角是直角的特殊平行四边形。实质上：
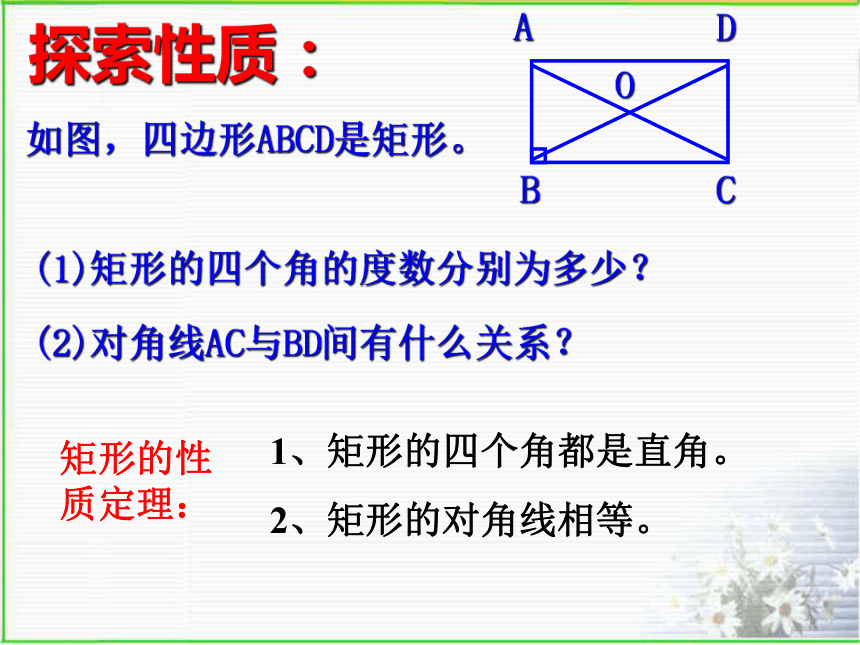
　　　矩形是特殊的平行四边形。如图，四边形ABCD是矩形。O探索性质：(1)矩形的四个角的度数分别为多少？(2)对角线AC与BD间有什么关系？1、矩形的四个角都是直角。
2、矩形的对角线相等。
矩形的性质定理： ABCD已知：四边形ABCD是矩形，∠A＝900 。 求证：∠A= ∠B = ∠C=∠D=900 。 证明：∵ 四边形ABCD是矩形∴ AD∥BC∴ ∠A+ ∠B=1800又∵ ∠A＝900∴ ∠B ＝900又∵ ∠A = ∠C， ∠B = ∠D（矩形的对角相等）∴ ∠A= ∠B = ∠C=∠D=900即 矩形的 四个角都是直角。定理1、矩形的四个角都是直角。ABCD已知：AC,BD是矩形的对角线。求证：AC=BD 。证明：在矩形ABCD中，
∵ AB=CD(平行四边形的对边相等）
∠BAD=∠CDA=Rt∠（矩形的每个角都是直角） AD=DA∴ Rt△BAD≌ Rt△CDA(SAS)∴ AC=BD.即 矩形的对角线相等。思考：性质定理（2）的证明还可以采用什么方法？
定理2：矩形的对角线相等。证法二：O已知：AC,BD是矩形的对角线。求证：AC=BD 。 在矩形ABCD中，AC、BD是对角线即 BD = AC .∵ ∠ABC=∠ADC=Rt∠, OA=OC, OB=OD邻边：互相垂直（3）对角线：（1）边：（共性）（共性）（特性）（特性）（特性）（共性）O矩形特征：运用性质： 思考：如图，在矩形ABCD中，对角线AC、BD相交于点O.
（1）你能发现ＯＡ，ＯＢ，ＯＣ，ＯＤ这四条线段有什 么关系吗？
（2）图中有多少个等腰三角形？有多少对全等三角形？
解：（1） OA=OB=OC=OD ;（2）有四个等腰三角形；
有八对全等三角形： △AOB≌△COD, △AOD≌△BOC, △ABD≌△ACD, △ABD ≌△BCD, △ABD ≌△ABC,
△ACD≌△BCD , △ACD ≌△ABC , △ABC ≌△BCD .
例1、已知：如图：在矩形ABCD中，对角线AC、BD相交于点O, ∠AOD=120°， AB=4cm。
（1）判断△AOB的形状；
（2） 求 BD与AD的长。解: (1)
(2)∵ AB=4cm,
∴AC=BD=2AB=8cm. 在Rt△BAD中，根据勾股定理，得： ∴答：BD=8cm，学以致用： 如图，矩形ABCD的对角线AC、BD相交于O，∠BOC=2 ∠ AOB，若AC=6cm, 试求AB的长。
想一想：矩形是轴对称图形吗？如果是，它有几条对称轴?
是中心对称图形吗？矩形是轴对称图形，它有两条对称轴。矩形也是中心对称图形，它的对称中心是对角线的交点。练一练：(1) 已知矩形的周长是14cm，相邻两边的差是1cm，那么这个矩形的面积是多少？(2) 矩形的一对角线与一边的夹角是50o，则这两条对角线所夹的锐角为_______80o12cm2（3）已知:如图,过矩形ABCD的顶点作CD//BD，交 AB的延长线于E。 求证：∠CAE=∠CEA.(4) 如图，在矩形ABCD中，DE⊥AC，
，那么30o体会.分享通过今天的学习，你能谈谈你的收获吗？
还有哪些困惑？小结：矩形的性质：（特性）（共性）谢谢大家！