5.6三角形的中位线[下学期]

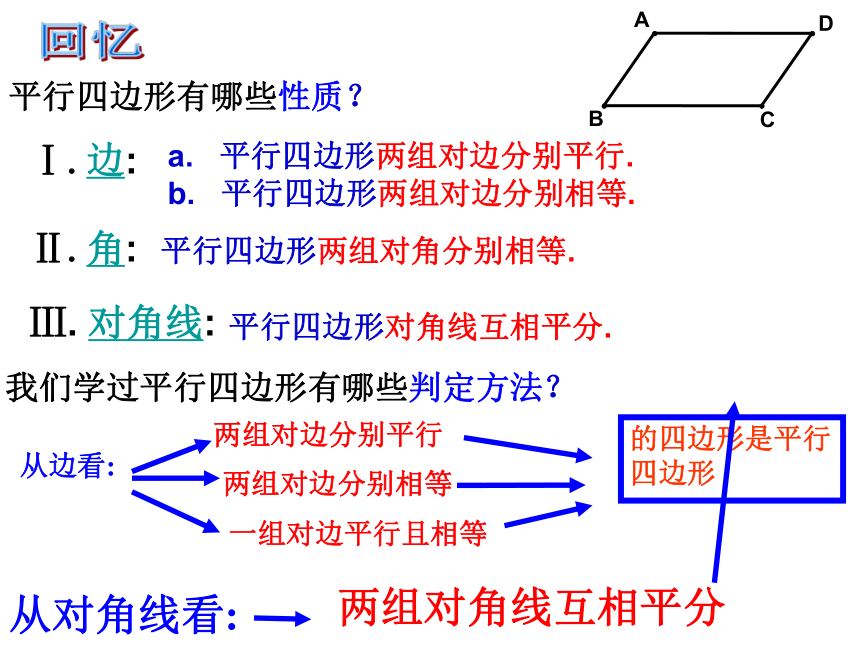
课件29张PPT。回忆平行四边形有哪些性质？ a. 平行四边形两组对边分别平行.
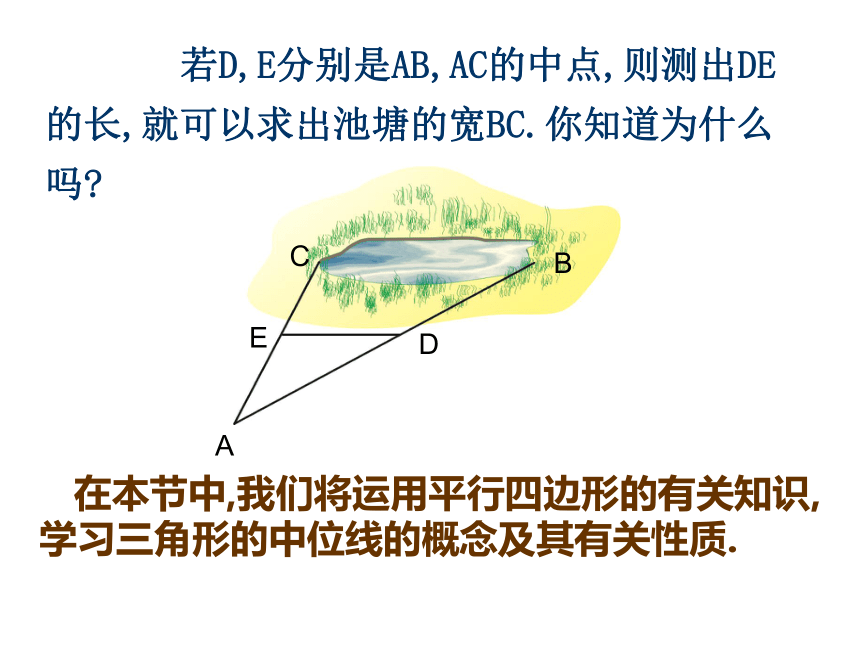
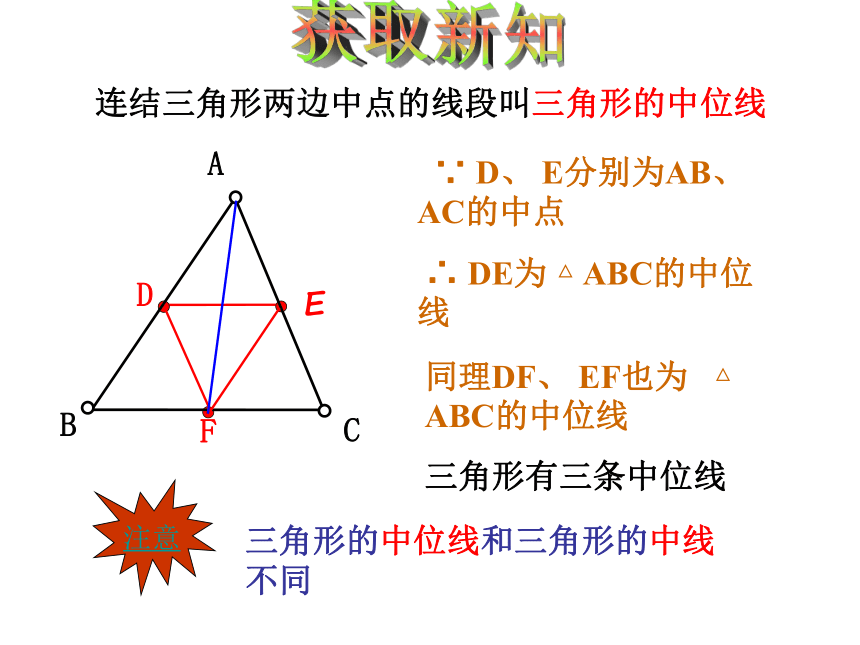
b. 平行四边形两组对边分别相等.平行四边形两组对角分别相等.平行四边形对角线互相平分.我们学过平行四边形有哪些判定方法？ 从边看: 两组对边分别平行 两组对边分别相等 一组对边平行且相等 的四边形是平行四边形 从对角线看: 两组对角线互相平分 回顾平行四边形的性质定理和判定定理1四边形是平行四边形两组对边平行且相等四边形是平行四边形对角线互相平分2123四边形是平行四边形四边形是平行四边形四边形是平行四边形两组对边分别相等对角线互相平分一组对边平行并且相等平行四边形的对角相等、邻角互补两组对边分别平行的四边形是平行四边形三角形中位线 若D,E分别是AB,AC的中点,则测出DE的长,就可以求出池塘的宽BC.你知道为什么吗? 在本节中,我们将运用平行四边形的有关知识,学习三角形的中位线的概念及其有关性质.获取新知连结三角形两边中点的线段叫三角形的中位线三角形有三条中位线 ∵ D、 E分别为AB、 AC的中点
∴ DE为 △ ABC的中位线
三角形的中位线和三角形的中线不同同理DF、 EF也为 △ ABC的中位线
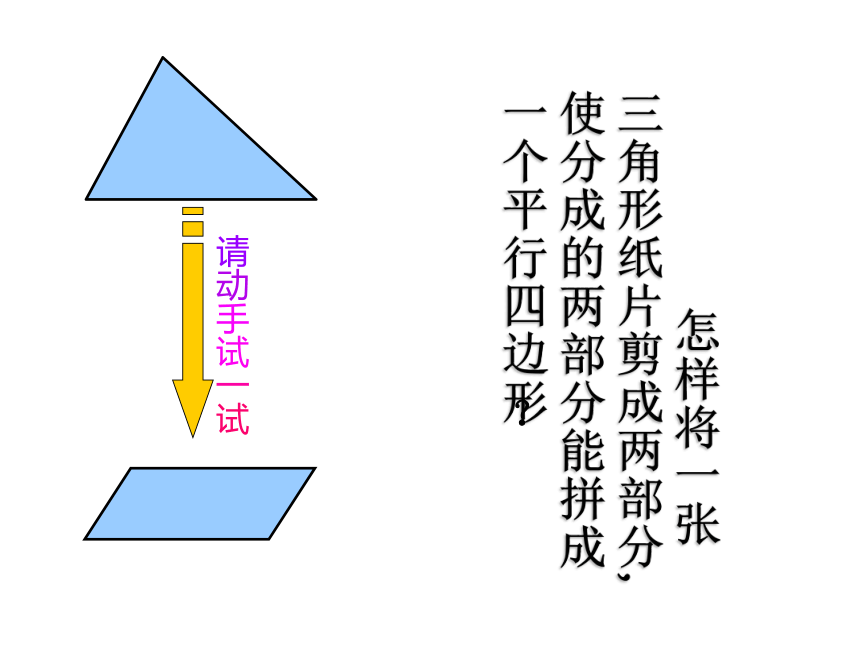
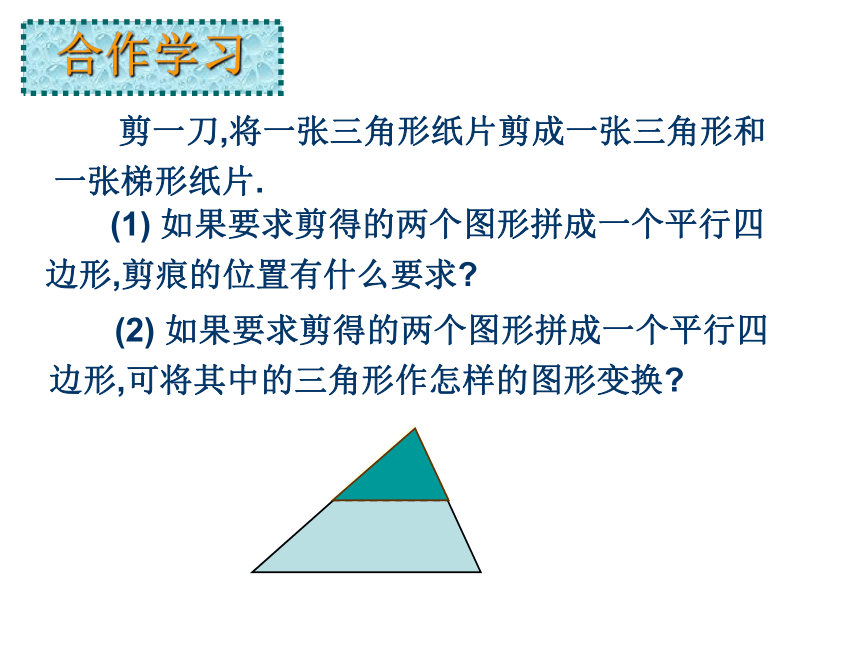
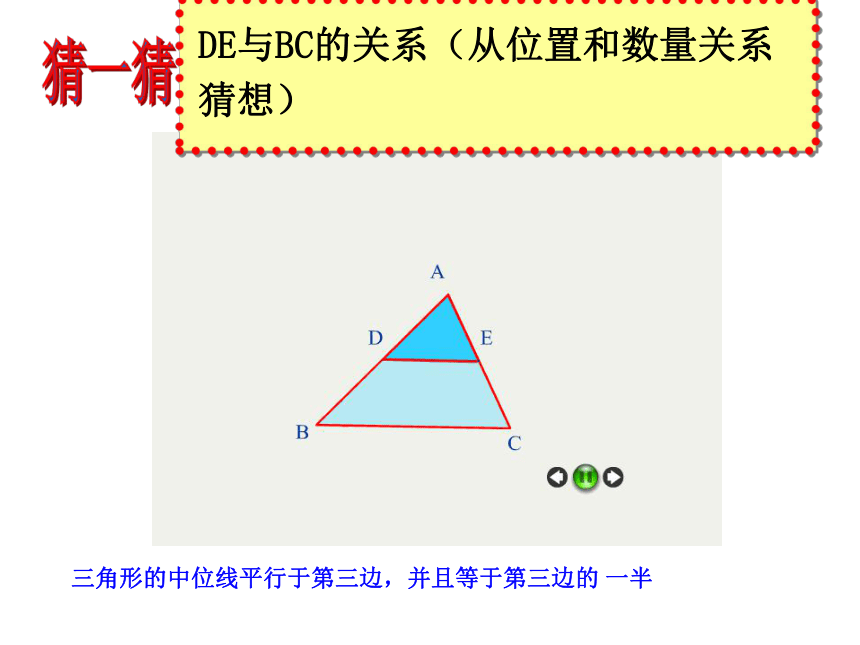
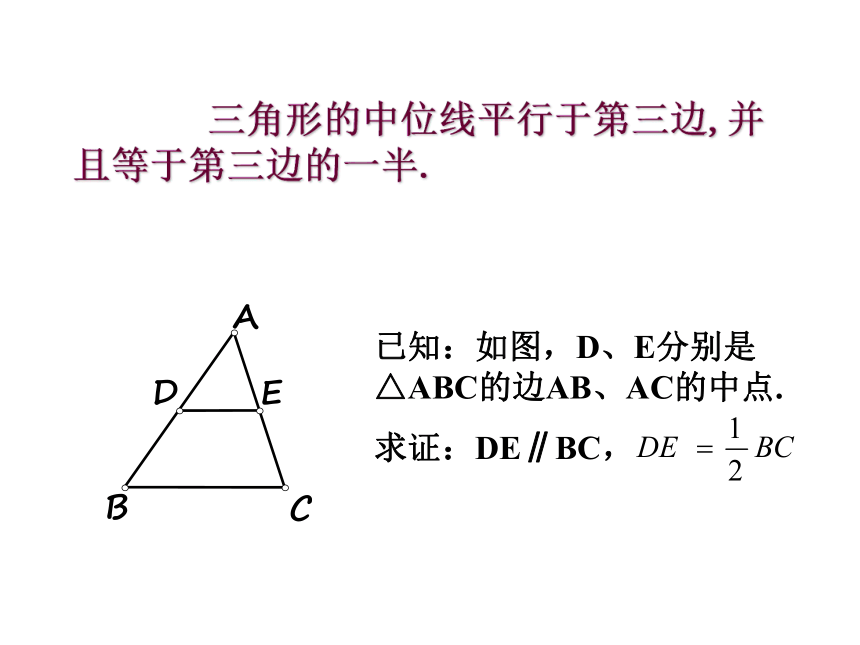
EDF 怎样将一张三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形请动手试一试？ 合作学习 剪一刀,将一张三角形纸片剪成一张三角形和一张梯形纸片. (2) 如果要求剪得的两个图形拼成一个平行四边形,可将其中的三角形作怎样的图形变换? (1) 如果要求剪得的两个图形拼成一个平行四边形,剪痕的位置有什么要求?猜一猜DE与BC的关系（从位置和数量关系猜想）三角形的中位线平行于第三边，并且等于第三边的 一半 三角形的中位线平行于第三边,并且等于第三边的一半. 三角形的中位线平行于第三边,并且等于第三边的一半. 分析 因为E是AC的中点,可以考虑以E为旋转中心,把⊿ADE旋转1800,得到⊿CFE (为什么?)如图5-37这样就只需证明四边形BCFD是平行四边形.图5-37图5-36你还能不同的方法加以证明吗?三角形的中位线平行于第三边，并且等于第三边的 一半ABCDEF已知：在△ABC 中，DE是△ABC 的中位线
求证：DE ∥ BC，且DE=1/2BC 。 证明：如 图，延 长DE 到 F，使EF=DE ，连 结CF.
∵DE=EF 、∠AED=∠CEF 、AE=EC
∴△ADE ≌ △CFE
∴AD=FC 、∠A=∠ECF
∴AB∥FC
又AD=DB ∴BD∥CF且BD=CF
∴四边形BCFD是平行四边形
∴DE ∥ BC 且 DE=1/2BC
同一法定理证法二：过点C作AB的平行线交DE的延长线于F
∵CF∥AB，∴∠A=∠ECF
又AE=EC，∠AED=∠CEF
∴△ADE ≌ △CFE ∴AD=FC
又DB=AD，∴DB∥FC且DB=FC
∴四边形BCFD是平行四边形
∴DE ∥ BC 且 DE=1/2BC
证法三：如图，延 长DE 到 F，使EF=DE ，连 结CF.AF、DC
∵AE=EC ,EF=DE
∴四边形ADCF是平行四边形
∴AD∥FC且AD=FC
又D为AB中点，∴DB=FC
∴BD=CF 且DB∥FC
∴四边形BCFD是平行四边形
∴DE ∥ BC 且 DE=1/2BC
?ABCEDFABCEDF三角形中位线定理　　三角形的中位线平行于第三边，并且等于第三边的一半.几何语言：∵DE是△ABC的中位线（或AD=BD,AE=CE)
∴DE∥BC,且DE=1/2BC
(三角形的中位线平行于第三边,并且等于它的一半)
方法点拨：
在处理问题时,要求同时出现三角形及中位线
①有中点连线而无三角形,要作辅助线产生三角形
②有三角形而无中位线,要连结两边中点得中位线定 理 应 用：⑴定理为证明平行关系提供了新的工具
⑵定理为证明一条线段是另一条线段的2倍或 1/2提供了一个新的途径初显身手 三条中位线围成一个新的三角形，它与原来的三角形有无关系?哪方面有关系?(1) △DEF的周长与 △ABC的周长有什么关系?(2) △DEF的面积与 △ABC的面积有什么关系?1.如图1：在△ABC中，DE是中位线
（1）若∠ADE=60°，
则∠B= 度，为什么？
（2）若BC=8cm，
则DE= cm，为什么？ 2.如图2：在△ABC中，D、E、F分别
是各边中点
AB=6cm，AC=8cm，BC=10cm，
则△DEF的周长= cm图1图260412ABCD。。EBACD 。。E。F543再显身手 分析 由E,F,G,H分别是四边形ABCD各边的中点,联想到应用三角形的中位线定理来证明.例 已知:如图5-38,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.
求证: 四边形EFGH是平行四边形.证明: 连结AC.∵ EF是⊿ABC的中位线,∴四边形EFGH是平行四边形 (一组对边平行并且相等的四边形是增行四边形). 1.任意作一个三角形,然后用刻度尺作出它的中位线. 2.要测量B,C两地的距离,小明想出一个方法:在池塘外取点A,得到线段AB,AC,并取AB,AC的中点D,E,连结DE.只要测出
DE的长,就可以求得B,C两
地的距离.你认为这个方法
正确吗?请说明理由. 课内练习 课内练习 3.已知: 如图,DE,EF是⊿ABC的两条中位线.求证:四边形BFED是平行四边形. 4.如图,DE是⊿ABC的中位线,AF是BC边上的中线,DE和AF交于点O.求证:DE与AF互相平分. 例3：已知如图：在△ABC中，AB、BC、CA的中点分别是E、F、G，AD是高。求 证：∠EDG＝ ∠EFG。分析：EF是△ABC的中位线DG是Rt△ADC斜边上的中线∴EF＝DG你还想到了什么？问题3如图，已知CE、CB分别是△ABC, △ADC 的中线，且AB=AC，试说明CD=2CEABCED三角形中位线定理　　三角形的中位线平行于第三边，并且等于第三边的一半.几何语言：∵DE是△ABC的中位线（或AD=BD,AE=CE)
∴DE∥BC,且DE=1/2BC
(三角形的中位线平行于第三边,并且等于它的一半)
已知：在四边形ABCD中，E，F分别是对角线AC，BD的中点，M，N分别是AB，CD的中点。求证：EF与MN互相平分（5分）在四边形ABCD中，AB=CD，M，N，P分别AD，BC，BD的中点。求证：∠PNM=∠PMN（4分）在ΔABC中，D，E分别是AB、CD边上的中点。M、N分别是DB、BE边上的中点。AC=6，则MN=-------2分DE是RtΔABC的中位线，AF是斜边BC上的中线，则DE与AF有何数量关系？（3分）1、顺次连结所得四边形EFGH的各边中点，将得到一个怎样的四边形？再继续下去……你能得到什么结论?2、若四边形ABCD的对角线相等，那么顺次连结各边中点的四边形是一个怎样的四边形？对角线垂直呢？想一想