5.1.3.多边形 [下学期]

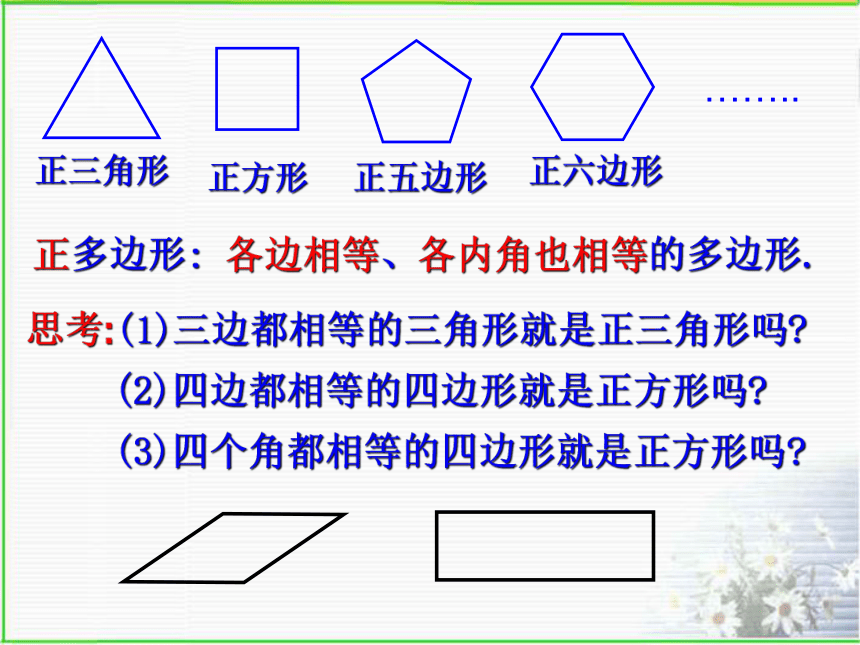
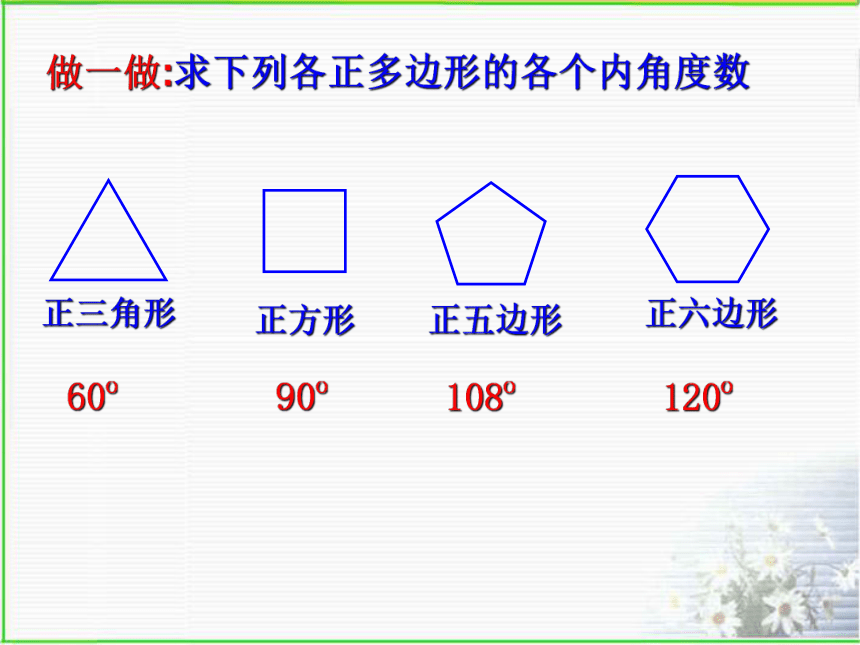
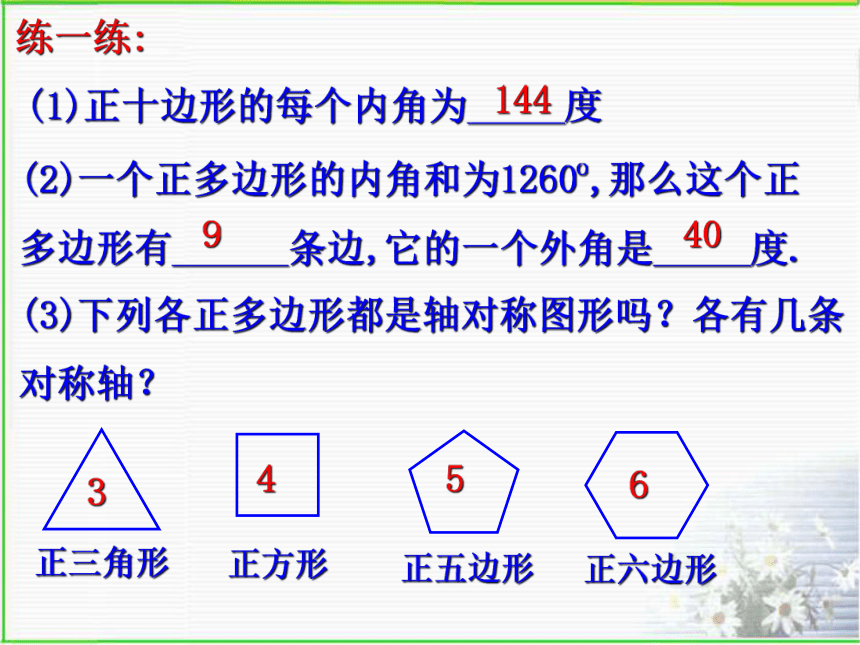
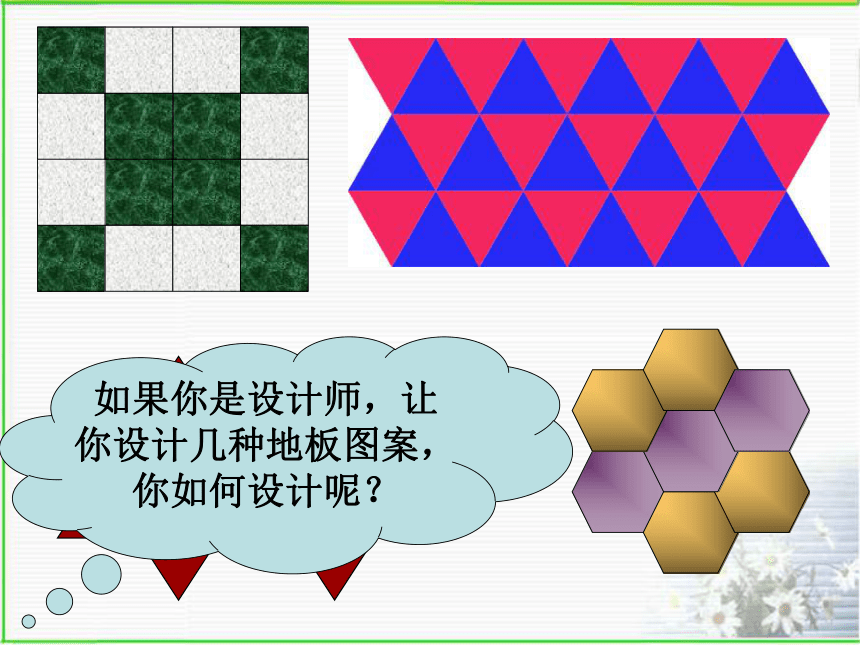
课件26张PPT。 好漂亮的路面!这是怎么铺设的? 一点空隙也没有.分水初级中学 胡利群　　由于规则的图形有许多优良的性质，匀称美观，常被人们用于图案设计和镶嵌平面.正多边形:各边相等、各内角也相等的多边形.思考:(1)三边都相等的三角形就是正三角形吗?(2)四边都相等的四边形就是正方形吗?(3)四个角都相等的四边形就是正方形吗?做一做:求下列各正多边形的各个内角度数60o90o108o120o练一练:(1)正十边形的每个内角为_____度144(2)一个正多边形的内角和为1260o,那么这个正多边形有______条边,它的一个外角是_____度.9403456如果你是设计师，让你设计几种地板图案，你如何设计呢？ 用形状和大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，这就是平面图形的镶嵌，又称平面图形的密铺.学一学镶嵌的两个条件：
1、全等的一种或几种平面图形；
2、无空隙、不重叠铺成一片。 探究
哪些图形可以镶嵌，
哪些图形不可以镶嵌？探究活动（一） 用形状、大小完全相同的三角形能否镶嵌平面？做一做 正三角形的平面镶嵌60°60°60°60°60°60°接点处的六个角和为360°结论：
形状、大小完全相同的任意
三角形能镶嵌平面。 通过探究我发现：1.任意全等的三角形都______密铺,
2.在每个拼接点处有___个角，而这___个角的和恰好是这个三角形的内角和的___倍，也就是它们的和为____，
可以六六两360o 探究活动（二） 用同一种四边形可以镶嵌平面吗？做一做 正方形的平面镶嵌90°结论：
形状、大小相同的任意四边形
能镶嵌平面★通过探究我发现：1.任意全等的四边形_____密铺.
2.在每个拼接点处有___个角，而这___个角的和恰好是这个四边形的四个内角之___,也就是它们的和为____.
可以四四和360o能密铺的图形在一个拼接
点处的特点： 1.各角之和等于360o,
2.相等的边互相重合。想一想结论 1议一议探究活动（三） 2.正六边形能镶嵌平面吗？说说理由。 1.正五边形能镶嵌平面吗？说说理由。 3.还能找到能镶嵌平面的其他正多 边形吗？做一做正五边形可以镶嵌平面吗？
能能能正三角形正方形正五边形正六边形643不能结论1：
可以用同一种正多边形密铺的图形只有
正三角形，正四边形，正六边形.结论2:
用一种形状、大小完全相同的三角形、四边形 也能进行平面镶嵌1、下列多边形一定不能进行平面镶嵌的是（ ）
A、三角形 B、正方形 C、任意四边形 D、正八边形2、用正方形一种图形进行平面镶嵌时，在它的一个顶点周围的
正方形的个数是（ ）

A、 3 B 、4 C、5 D 、63、如果只用一种正多边形作平面镶嵌，而且在每一个正多边形的
每一个顶点周围都有6个正多边形，则该正多边形的边数为（ ）
A、3 B、4 C、5 D、6DBA试一试探究活动(四)
----创意空间 用同一种平面图形如果不能密铺,用两种或者两种以上平面图形能不能镶嵌平面呢? 多种正边形镶嵌平面.例：用边长相等的正八边形和正方形能镶嵌平面吗？解：因为正八边形的内角为135o，正方形的内角为90o,由于135o×2+90o＝360o，所以两个正八边形和一个正方形能拼成一幅镶嵌图。体会.分享 能说说你这节课的收获和体验让大家与你分享吗？