【核心素养目标】1.2 有关三角函数的计算(2) 教学设计
文档属性
| 名称 | 【核心素养目标】1.2 有关三角函数的计算(2) 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 17:51:16 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙教版九年级下册数学1.2 有关三角函数的计算(2)教学设计
课题 1.2 有关三角函数的计算(2) 单元 第一单元 学科 数学 年级 九
教材分析 本节课是第二节第二课时的内容,主要内容是用计算器根据三角函数值求锐角的度数,本节课以求公路弯道的长为背景设计问题引入,目的在于说明由已知三角函数值求锐角也是解决现实生活中实际问题的需要,教学中要重视让围绕“合作学习”的三个问题进行思考、交流,由此感受学习由已知三角函数值求锐角的必要性和学习的价值,由此激发学习兴趣。
核心素养分析 遵循认知规律,为学生创造自主探究,合作交流的空间,为教师营造教学创新的氛围,为师生互动式教学提供丰富的资源。促进现代信息技术与数学课程的整合,改进教材的呈现方式,提高学生学习数学的兴趣。
学习目标 1.会根据锐角的三角函数值,借助科学计算器求锐角的大小。2.熟练运用计算器解决锐角三角函数中的问题。3.会把实际问题转化为解直角三角形问题,从而把实际问题转化为数学问题来解决。
重点 会根据锐角的三角函数值,借助科学计算器求锐角的大小.
难点 善于将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而利用所学知识把实际问题解决.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 想一想,怎样用计算器求锐角三角形的函数值?【算一算】用计算器求 cos 25°18′ 的值(精确到0.0001).方法一:第一步:按计算器上的键;第二步:输入角度值25,分值18(按键顺序:25 18 );第三步:按 “ = ” 号键,屏幕显示结果 0.904082549≈0.9041.方法二:第一步:先将角进行转化 25°18′ =25.3°第二步:按计算器上的键;第三步:输入角度值25.3(按键顺序:25.3);第四步:按 “ = ” 号键. 学生根据上一节课学的知识利用计算器计算三角函数值。 通过复习,激发学生学习动机和兴趣,吸引学生注意力,为引进新知识的学习做好心理准备。
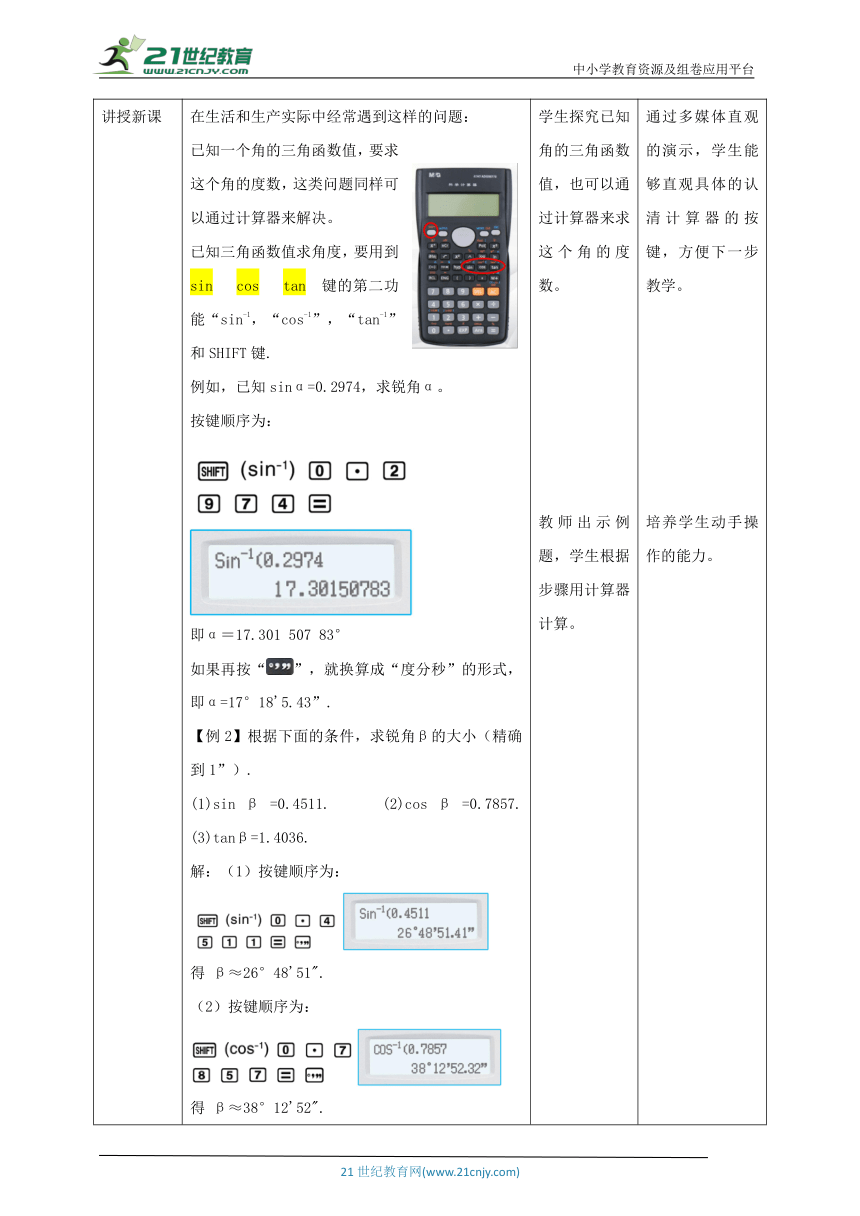
讲授新课 在生活和生产实际中经常遇到这样的问题:已知一个角的三角函数值,要求这个角的度数,这类问题同样可以通过计算器来解决。已知三角函数值求角度,要用到sin cos tan 键的第二功能“sin-1,“cos-1”,“tan-1”和SHIFT键.例如,已知sinα=0.2974,求锐角α。按键顺序为:即α=17.301 507 83°如果再按“”,就换算成“度分秒”的形式,即α=17°18'5.43”.【例2】根据下面的条件,求锐角β的大小(精确到1”).(1)sinβ=0.4511. (2)cosβ=0.7857. (3)tanβ=1.4036.解:(1)按键顺序为:得 β≈26°48'51".(2)按键顺序为:得 β≈38°12'52".(3)按键顺序为:得 β≈54°31'55".【总结归纳】由锐角三角函数值求锐角的度数与已知锐角求三角函数值的过程是互逆的,由锐角三角函数值求锐角的度数时应先按SHIFT键,一定要注意结果所要求的单位.【例3】已知圆弧形公路弯道的两端相距 200 m,圆弧半径为1km,你能求出弯道的长吗?如图,一段公路弯道呈圆弧形,测得弯道弧AB两端的距离为200 m,弧AB的半径为1000m。求弯道的长(精确到0.1m).分析:因为弧AB的半径已知,根据弧长公式l=nπR÷180,要求弯道弧AB的长,只要求出弧AB所对圆心角∠AOB的度数。解:作OC⊥AB,垂足为C,则OC平分∠AOB.在Rt△OCB中,BC=AB=100m,OB=1000m, 于是有sin∠BOC= .你能利用计算器求出∠BOC的度数吗?∵sin∠BOC=.∴∠BOC≈5.74°,∠AOB=5.74°×2=11.48°,∴弯道的长约为(11.48×π×1000)÷180≈200.3m 学生探究已知角的三角函数值,也可以通过计算器来求这个角的度数。教师出示例题,学生根据步骤用计算器计算。学生根据实际问题,转换成数学问题,并利用本节课所学知识解决问题。 通过多媒体直观的演示,学生能够直观具体的认清计算器的按键,方便下一步教学。培养学生动手操作的能力。学生能够运用已学知识解决问题,这样既能提高学生解决问题兴趣,又培养学生观察、分析、归纳问题、逻辑理解的能力。
课堂练习 1.已知sin A=0.981 6,运用科学计算器求锐角∠A时(在开机状态下),按下的第一个键是( D )A. B. C. D.2.已知sin A=0.356,则锐角A的度数大约为( B ).A.20° B.21° C.22° D.23°3.如果cos α=tan 30°,那么锐角α的取值范围是( C ).A.0<α<30° B.30°<α<45°C.45°<α<60° D.60°<α<90°4.已知下列锐角三角函数值,用计算器求其相应的锐角度数(结果精确到1′).(1)sin A=0.627 5,则∠A≈38°52′;(2)cos A=0.625 2,则∠A≈51°18′;(3)tan A=4.842 5,则∠A≈78°20′.5.在△ABC中,sin A=cos (90°-∠C)=,则△ABC的形状是( B )A.锐角三角形 B.直角三角形C.钝角三角形 D.不确定6.在Rt△ABC中,∠C=90°,a,b分别是∠A,∠B的对边长,a:b=3∶4,运用计算器计算∠A的度数(精确到1°)为( B ).A.30° B.37° C.38° D.39° 学生做练习,教师订正答案。 通过各种形式的练习,进一步提高学生学习兴趣,使 学生的认知结构更加完善。同时强化本课的教学重点,突破教学难点。
课堂小结 本节课你学到了什么?1.已知一个角的三角函数值,要求这个角的度数,也可以通过计算器来解决。2.由锐角三角函数值求锐角的度数与已知锐角求三角函数值的过程是互逆的,由锐角三角函数值求锐角的度数时应先按SHIFT键,一定要注意结果所要求的单位. 学生总结本节课所学知识。
板书 课题:1.2 有关三角函数的计算(2) 一、通过计算器计算角的度数.二、例题讲解
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
浙教版九年级下册数学1.2 有关三角函数的计算(2)教学设计
课题 1.2 有关三角函数的计算(2) 单元 第一单元 学科 数学 年级 九
教材分析 本节课是第二节第二课时的内容,主要内容是用计算器根据三角函数值求锐角的度数,本节课以求公路弯道的长为背景设计问题引入,目的在于说明由已知三角函数值求锐角也是解决现实生活中实际问题的需要,教学中要重视让围绕“合作学习”的三个问题进行思考、交流,由此感受学习由已知三角函数值求锐角的必要性和学习的价值,由此激发学习兴趣。
核心素养分析 遵循认知规律,为学生创造自主探究,合作交流的空间,为教师营造教学创新的氛围,为师生互动式教学提供丰富的资源。促进现代信息技术与数学课程的整合,改进教材的呈现方式,提高学生学习数学的兴趣。
学习目标 1.会根据锐角的三角函数值,借助科学计算器求锐角的大小。2.熟练运用计算器解决锐角三角函数中的问题。3.会把实际问题转化为解直角三角形问题,从而把实际问题转化为数学问题来解决。
重点 会根据锐角的三角函数值,借助科学计算器求锐角的大小.
难点 善于将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而利用所学知识把实际问题解决.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 想一想,怎样用计算器求锐角三角形的函数值?【算一算】用计算器求 cos 25°18′ 的值(精确到0.0001).方法一:第一步:按计算器上的键;第二步:输入角度值25,分值18(按键顺序:25 18 );第三步:按 “ = ” 号键,屏幕显示结果 0.904082549≈0.9041.方法二:第一步:先将角进行转化 25°18′ =25.3°第二步:按计算器上的键;第三步:输入角度值25.3(按键顺序:25.3);第四步:按 “ = ” 号键. 学生根据上一节课学的知识利用计算器计算三角函数值。 通过复习,激发学生学习动机和兴趣,吸引学生注意力,为引进新知识的学习做好心理准备。
讲授新课 在生活和生产实际中经常遇到这样的问题:已知一个角的三角函数值,要求这个角的度数,这类问题同样可以通过计算器来解决。已知三角函数值求角度,要用到sin cos tan 键的第二功能“sin-1,“cos-1”,“tan-1”和SHIFT键.例如,已知sinα=0.2974,求锐角α。按键顺序为:即α=17.301 507 83°如果再按“”,就换算成“度分秒”的形式,即α=17°18'5.43”.【例2】根据下面的条件,求锐角β的大小(精确到1”).(1)sinβ=0.4511. (2)cosβ=0.7857. (3)tanβ=1.4036.解:(1)按键顺序为:得 β≈26°48'51".(2)按键顺序为:得 β≈38°12'52".(3)按键顺序为:得 β≈54°31'55".【总结归纳】由锐角三角函数值求锐角的度数与已知锐角求三角函数值的过程是互逆的,由锐角三角函数值求锐角的度数时应先按SHIFT键,一定要注意结果所要求的单位.【例3】已知圆弧形公路弯道的两端相距 200 m,圆弧半径为1km,你能求出弯道的长吗?如图,一段公路弯道呈圆弧形,测得弯道弧AB两端的距离为200 m,弧AB的半径为1000m。求弯道的长(精确到0.1m).分析:因为弧AB的半径已知,根据弧长公式l=nπR÷180,要求弯道弧AB的长,只要求出弧AB所对圆心角∠AOB的度数。解:作OC⊥AB,垂足为C,则OC平分∠AOB.在Rt△OCB中,BC=AB=100m,OB=1000m, 于是有sin∠BOC= .你能利用计算器求出∠BOC的度数吗?∵sin∠BOC=.∴∠BOC≈5.74°,∠AOB=5.74°×2=11.48°,∴弯道的长约为(11.48×π×1000)÷180≈200.3m 学生探究已知角的三角函数值,也可以通过计算器来求这个角的度数。教师出示例题,学生根据步骤用计算器计算。学生根据实际问题,转换成数学问题,并利用本节课所学知识解决问题。 通过多媒体直观的演示,学生能够直观具体的认清计算器的按键,方便下一步教学。培养学生动手操作的能力。学生能够运用已学知识解决问题,这样既能提高学生解决问题兴趣,又培养学生观察、分析、归纳问题、逻辑理解的能力。
课堂练习 1.已知sin A=0.981 6,运用科学计算器求锐角∠A时(在开机状态下),按下的第一个键是( D )A. B. C. D.2.已知sin A=0.356,则锐角A的度数大约为( B ).A.20° B.21° C.22° D.23°3.如果cos α=tan 30°,那么锐角α的取值范围是( C ).A.0<α<30° B.30°<α<45°C.45°<α<60° D.60°<α<90°4.已知下列锐角三角函数值,用计算器求其相应的锐角度数(结果精确到1′).(1)sin A=0.627 5,则∠A≈38°52′;(2)cos A=0.625 2,则∠A≈51°18′;(3)tan A=4.842 5,则∠A≈78°20′.5.在△ABC中,sin A=cos (90°-∠C)=,则△ABC的形状是( B )A.锐角三角形 B.直角三角形C.钝角三角形 D.不确定6.在Rt△ABC中,∠C=90°,a,b分别是∠A,∠B的对边长,a:b=3∶4,运用计算器计算∠A的度数(精确到1°)为( B ).A.30° B.37° C.38° D.39° 学生做练习,教师订正答案。 通过各种形式的练习,进一步提高学生学习兴趣,使 学生的认知结构更加完善。同时强化本课的教学重点,突破教学难点。
课堂小结 本节课你学到了什么?1.已知一个角的三角函数值,要求这个角的度数,也可以通过计算器来解决。2.由锐角三角函数值求锐角的度数与已知锐角求三角函数值的过程是互逆的,由锐角三角函数值求锐角的度数时应先按SHIFT键,一定要注意结果所要求的单位. 学生总结本节课所学知识。
板书 课题:1.2 有关三角函数的计算(2) 一、通过计算器计算角的度数.二、例题讲解
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
