【新课标】1.2 有关三角函数的计算(2) 课件(共25张PPT)
文档属性
| 名称 | 【新课标】1.2 有关三角函数的计算(2) 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-06 17:52:41 | ||
图片预览






文档简介
(共25张PPT)
1.2 有关三角函数的计算(2)
浙教版九年级下册
教学目标
1.会根据锐角的三角函数值,借助科学计算器求锐角的大小.
2.熟练运用计算器解决锐角三角函数中的问题.
3.会把实际问题转化为解直角三角形问题,从而把实际问题转化为数学问题来解决.
教学重难点
重点:
会根据锐角的三角函数值,借助科学计算器求锐角的大小.
难点:
善于将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而利用所学知识把实际问题解决.
新知导入
想一想,怎样用计算器求锐角三角形的函数值?
【算一算】用计算器求 cos 25°18′ 的值(精确到0.0001).
第二步:输入角度值25,分值18
(按键顺序:25 18 );
方法一:第一步:按计算器上的 键;
第三步:按 “ = ” 号键,屏幕显示结果
0.904082549≈0.9041.
新知导入
想一想,怎样用计算器求锐角三角形的函数值?
【算一算】用计算器求 cos 25°18′ 的值(精确到0.0001).
方法二:第一步:先将角进行转化 25°18′ =25.3°
第四步:按 “ = ” 号键.
第三步:输入角度值25.3(按键顺序:25.3 );
第二步:按计算器上的 键;
新知讲解
在生活和生产实际中经常遇到这样的问题:
已知一个角的三角函数值,要求这个角的度数,这类问题同样可以通过计算器来解决。
已知三角函数值求角度,要用到
sin cos tan 键的第二功能
“sin-1,“cos-1”,“tan-1”和SHIFT键.
新知讲解
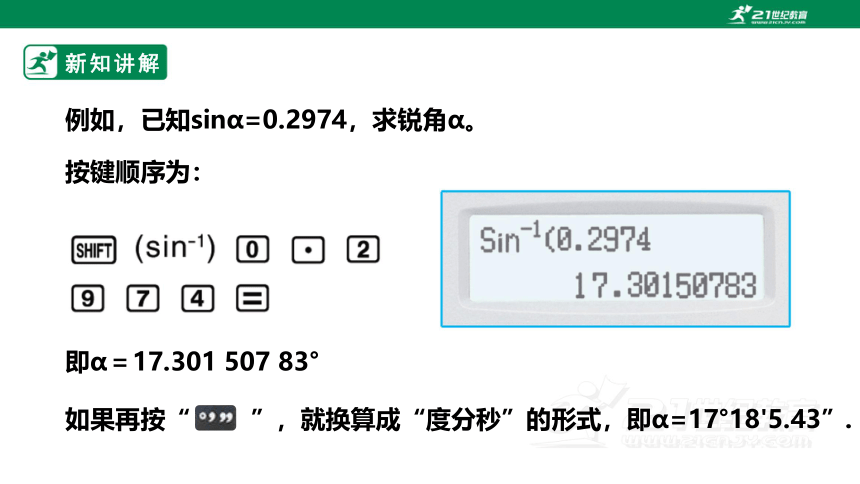
例如,已知sinα=0.2974,求锐角α。
按键顺序为:
即α=17.301 507 83°
如果再按“ ”,就换算成“度分秒”的形式,即α=17°18'5.43”.
新知讲解
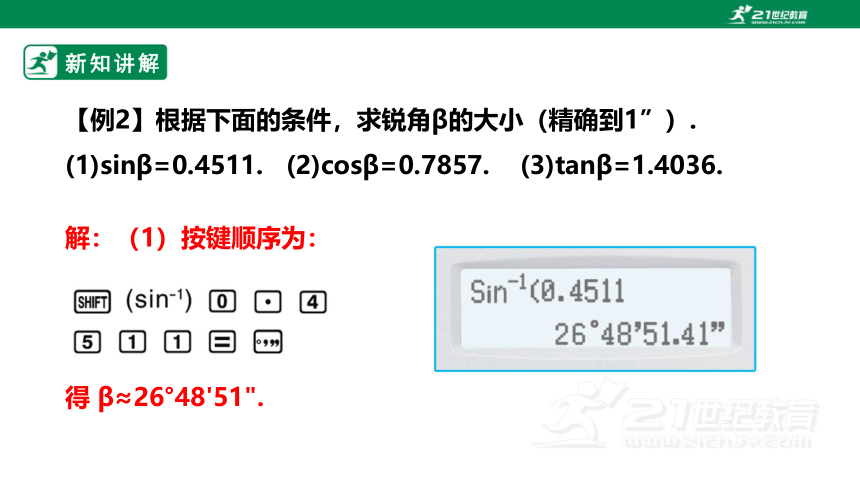
【例2】根据下面的条件,求锐角β的大小(精确到1”).
(1)sinβ=0.4511. (2)cosβ=0.7857. (3)tanβ=1.4036.
解:(1)按键顺序为:
得 β≈26°48'51".
新知讲解
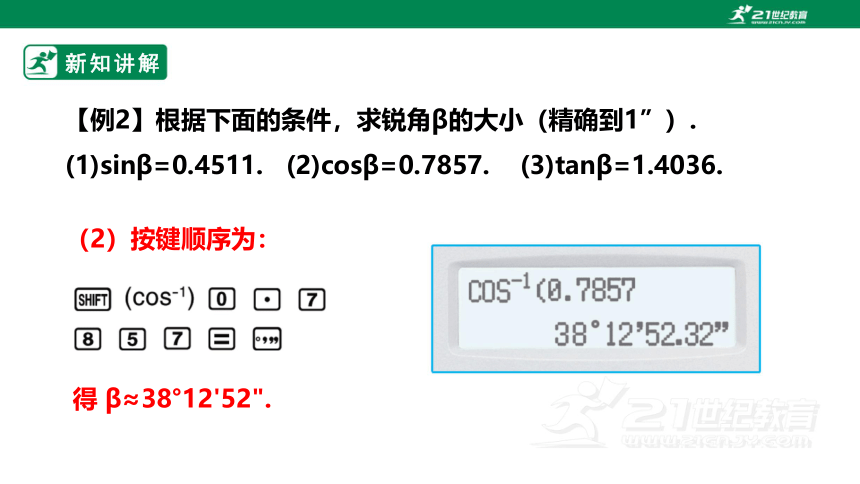
【例2】根据下面的条件,求锐角β的大小(精确到1”).
(1)sinβ=0.4511. (2)cosβ=0.7857. (3)tanβ=1.4036.
(2)按键顺序为:
得 β≈38°12'52".
新知讲解
【例2】根据下面的条件,求锐角β的大小(精确到1”).
(1)sinβ=0.4511. (2)cosβ=0.7857. (3)tanβ=1.4036.
(3)按键顺序为:
得 β≈54°31'55".
新知讲解
【总结归纳】
由锐角三角函数值求锐角的度数与已知锐角求三角函数值的过程是互逆的,由锐角三角函数值求锐角的度数时应先按SHIFT键,一定要注意结果所要求的单位.
新知讲解
【例3】已知圆弧形公路弯道的两端相距 200 m,圆弧半径为1km,你能求出弯道的长吗?
新知讲解
【例3】如图,一段公路弯道呈圆弧形,测得弯道弧AB两端的距离为200 m,弧AB的半径为1000m。求弯道的长(精确到0.1m).
分析:因为弧AB的半径已知,根据弧长公式l=nπR÷180,要求弯道弧AB的长,只要求出弧AB所对圆心角∠AOB的度数。
新知讲解
【例3】如图,一段公路弯道呈圆弧形,测得弯道弧AB两端的距离为200 m,弧AB的半径为1000m。求弯道的长(精确到0.1m).
解:作OC⊥AB,垂足为C,则OC平分∠AOB.
在Rt△OCB中,BC= AB=100m,OB=1000m, 于是有sin∠BOC= .
你能利用计算器求出∠BOC的度数吗?
新知讲解
【例3】如图,一段公路弯道呈圆弧形,测得弯道弧AB两端的距离为200 m,弧AB的半径为1000m。求弯道的长(精确到0.1m).
∵sin∠BOC= .
∴∠BOC≈5.74°,∠AOB=5.74°×2=11.48°,
∴弯道的长约为
(11.48×π×1000)÷180≈200.3m
课堂练习
D
2.已知sin A=0.356,则锐角A的度数大约为( ).
A.20° B.21° C.22° D.23°
B
课堂练习
3.如果cos α=tan 30°,那么锐角α的取值范围是( ).
A.0<α<30°
B.30°<α<45°
C.45°<α<60°
D.60°<α<90°
C
课堂练习
4.已知下列锐角三角函数值,用计算器求其相应的锐角度数(结果精确到1′).
(1)sin A=0.627 5,则∠A≈________;
(2)cos A=0.625 2,则∠A≈________;
(3)tan A=4.842 5,则∠A≈________.
38°52′
51°18′
78°20′
课堂练习
5.在△ABC中,sin A=cos (90°-∠C)= ,则△ABC的形状是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不确定
B
课堂练习
6.在Rt△ABC中,∠C=90°,a,b分别是∠A,∠B的对边长,
a∶b=3∶4,运用计算器计算∠A的度数(精确到1°)为( ).
A.30°
B.37°
C.38°
D.39°
B
课堂总结
本节课你学到了什么?
1.已知一个角的三角函数值,要求这个角的度数,也可以通过计算器来解决.
2.由锐角三角函数值求锐角的度数与已知锐角求三角函数值的过程是互逆的,由锐角三角函数值求锐角的度数时应先按SHIFT键,一定要注意结果所要求的单位.
板书设计
课题:1.2 有关三角函数的计算(2)
教师板演区
学生展示区
一、通过计算器计算角的度数.
二、例题讲解
作业布置
课本 P16 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.2 有关三角函数的计算(2)
浙教版九年级下册
教学目标
1.会根据锐角的三角函数值,借助科学计算器求锐角的大小.
2.熟练运用计算器解决锐角三角函数中的问题.
3.会把实际问题转化为解直角三角形问题,从而把实际问题转化为数学问题来解决.
教学重难点
重点:
会根据锐角的三角函数值,借助科学计算器求锐角的大小.
难点:
善于将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而利用所学知识把实际问题解决.
新知导入
想一想,怎样用计算器求锐角三角形的函数值?
【算一算】用计算器求 cos 25°18′ 的值(精确到0.0001).
第二步:输入角度值25,分值18
(按键顺序:25 18 );
方法一:第一步:按计算器上的 键;
第三步:按 “ = ” 号键,屏幕显示结果
0.904082549≈0.9041.
新知导入
想一想,怎样用计算器求锐角三角形的函数值?
【算一算】用计算器求 cos 25°18′ 的值(精确到0.0001).
方法二:第一步:先将角进行转化 25°18′ =25.3°
第四步:按 “ = ” 号键.
第三步:输入角度值25.3(按键顺序:25.3 );
第二步:按计算器上的 键;
新知讲解
在生活和生产实际中经常遇到这样的问题:
已知一个角的三角函数值,要求这个角的度数,这类问题同样可以通过计算器来解决。
已知三角函数值求角度,要用到
sin cos tan 键的第二功能
“sin-1,“cos-1”,“tan-1”和SHIFT键.
新知讲解
例如,已知sinα=0.2974,求锐角α。
按键顺序为:
即α=17.301 507 83°
如果再按“ ”,就换算成“度分秒”的形式,即α=17°18'5.43”.
新知讲解
【例2】根据下面的条件,求锐角β的大小(精确到1”).
(1)sinβ=0.4511. (2)cosβ=0.7857. (3)tanβ=1.4036.
解:(1)按键顺序为:
得 β≈26°48'51".
新知讲解
【例2】根据下面的条件,求锐角β的大小(精确到1”).
(1)sinβ=0.4511. (2)cosβ=0.7857. (3)tanβ=1.4036.
(2)按键顺序为:
得 β≈38°12'52".
新知讲解
【例2】根据下面的条件,求锐角β的大小(精确到1”).
(1)sinβ=0.4511. (2)cosβ=0.7857. (3)tanβ=1.4036.
(3)按键顺序为:
得 β≈54°31'55".
新知讲解
【总结归纳】
由锐角三角函数值求锐角的度数与已知锐角求三角函数值的过程是互逆的,由锐角三角函数值求锐角的度数时应先按SHIFT键,一定要注意结果所要求的单位.
新知讲解
【例3】已知圆弧形公路弯道的两端相距 200 m,圆弧半径为1km,你能求出弯道的长吗?
新知讲解
【例3】如图,一段公路弯道呈圆弧形,测得弯道弧AB两端的距离为200 m,弧AB的半径为1000m。求弯道的长(精确到0.1m).
分析:因为弧AB的半径已知,根据弧长公式l=nπR÷180,要求弯道弧AB的长,只要求出弧AB所对圆心角∠AOB的度数。
新知讲解
【例3】如图,一段公路弯道呈圆弧形,测得弯道弧AB两端的距离为200 m,弧AB的半径为1000m。求弯道的长(精确到0.1m).
解:作OC⊥AB,垂足为C,则OC平分∠AOB.
在Rt△OCB中,BC= AB=100m,OB=1000m, 于是有sin∠BOC= .
你能利用计算器求出∠BOC的度数吗?
新知讲解
【例3】如图,一段公路弯道呈圆弧形,测得弯道弧AB两端的距离为200 m,弧AB的半径为1000m。求弯道的长(精确到0.1m).
∵sin∠BOC= .
∴∠BOC≈5.74°,∠AOB=5.74°×2=11.48°,
∴弯道的长约为
(11.48×π×1000)÷180≈200.3m
课堂练习
D
2.已知sin A=0.356,则锐角A的度数大约为( ).
A.20° B.21° C.22° D.23°
B
课堂练习
3.如果cos α=tan 30°,那么锐角α的取值范围是( ).
A.0<α<30°
B.30°<α<45°
C.45°<α<60°
D.60°<α<90°
C
课堂练习
4.已知下列锐角三角函数值,用计算器求其相应的锐角度数(结果精确到1′).
(1)sin A=0.627 5,则∠A≈________;
(2)cos A=0.625 2,则∠A≈________;
(3)tan A=4.842 5,则∠A≈________.
38°52′
51°18′
78°20′
课堂练习
5.在△ABC中,sin A=cos (90°-∠C)= ,则△ABC的形状是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不确定
B
课堂练习
6.在Rt△ABC中,∠C=90°,a,b分别是∠A,∠B的对边长,
a∶b=3∶4,运用计算器计算∠A的度数(精确到1°)为( ).
A.30°
B.37°
C.38°
D.39°
B
课堂总结
本节课你学到了什么?
1.已知一个角的三角函数值,要求这个角的度数,也可以通过计算器来解决.
2.由锐角三角函数值求锐角的度数与已知锐角求三角函数值的过程是互逆的,由锐角三角函数值求锐角的度数时应先按SHIFT键,一定要注意结果所要求的单位.
板书设计
课题:1.2 有关三角函数的计算(2)
教师板演区
学生展示区
一、通过计算器计算角的度数.
二、例题讲解
作业布置
课本 P16 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
