【新课标】1.3 解直角三角形(1) 课件(共25张PPT)
文档属性
| 名称 | 【新课标】1.3 解直角三角形(1) 课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-07 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
1.3 解直角三角形(1)
浙教版九年级下册
教学目标
1.运用锐角三角函数、勾股定理等知识解决在直角三角形中,由已知的一些边、角,求出另一些边角的问题的过程,了解解直角三角形的概念.
2.会运用锐角三角函数、勾股定理等知识解直角三角形,以及解决与直角三角形有关的简单实际问题.
教学重难点
重点:
掌握运用三角函数解直角三角形的方法.
难点:
解直角三角形的过程中,由已知条件求某条边或某个角的方法,以及求这些边、角的顺序往往不唯一,学会如何选择较优的方法和求解顺序。
新知导入
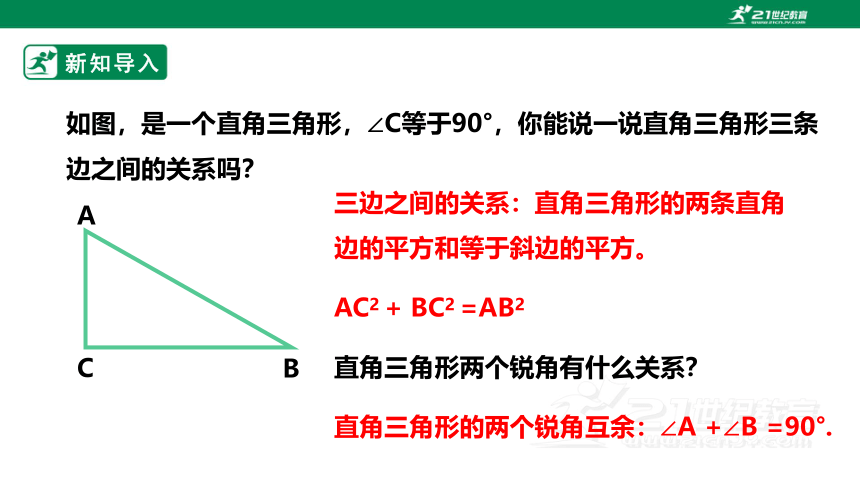
如图,是一个直角三角形,∠C等于90°,你能说一说直角三角形三条边之间的关系吗?
A
C
B
三边之间的关系:直角三角形的两条直角边的平方和等于斜边的平方。
AC2 + BC2 =AB2
直角三角形两个锐角有什么关系?
直角三角形的两个锐角互余:∠A +∠B =90°.
新知导入
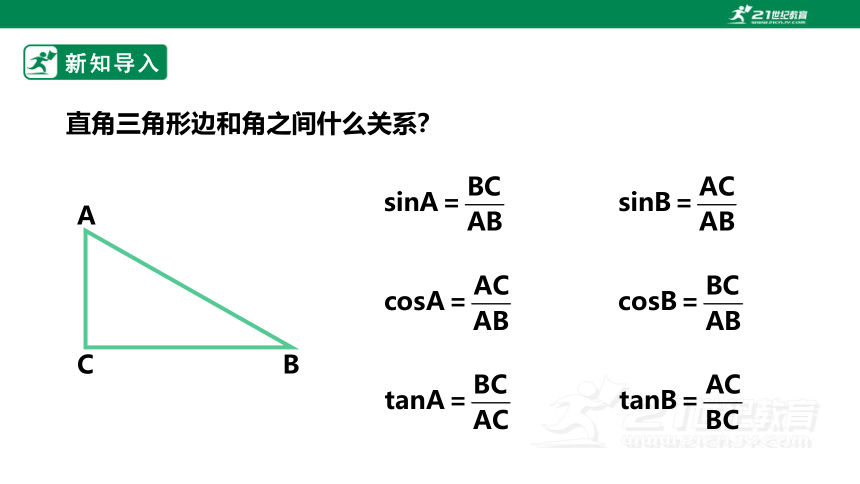
直角三角形边和角之间什么关系?
A
C
B
新知讲解
在日常生活和生产实践中,人们经常遇到有关三角形的边长与角度的
计算.
在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.
新知讲解
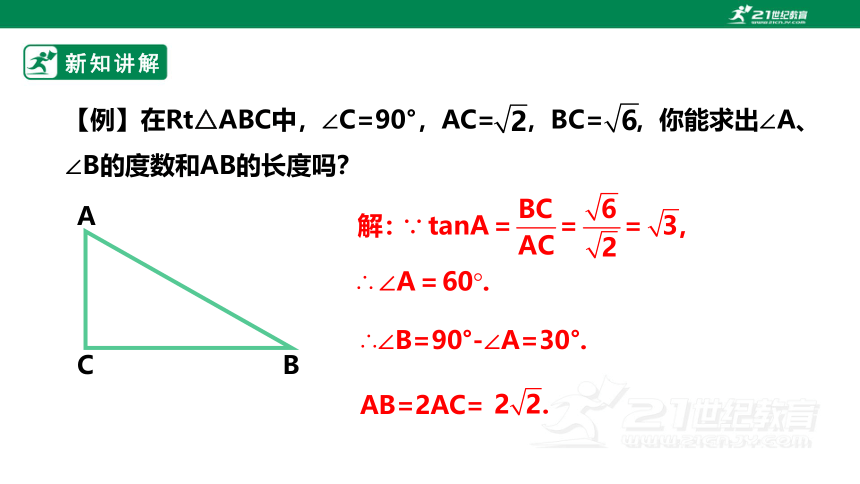
【例】在Rt△ABC中,∠C=90°,AC= ,BC= ,你能求出∠A、∠B的度数和AB的长度吗?
A
C
B
∴∠B=90°-∠A=30°.
AB=2AC=
新知讲解
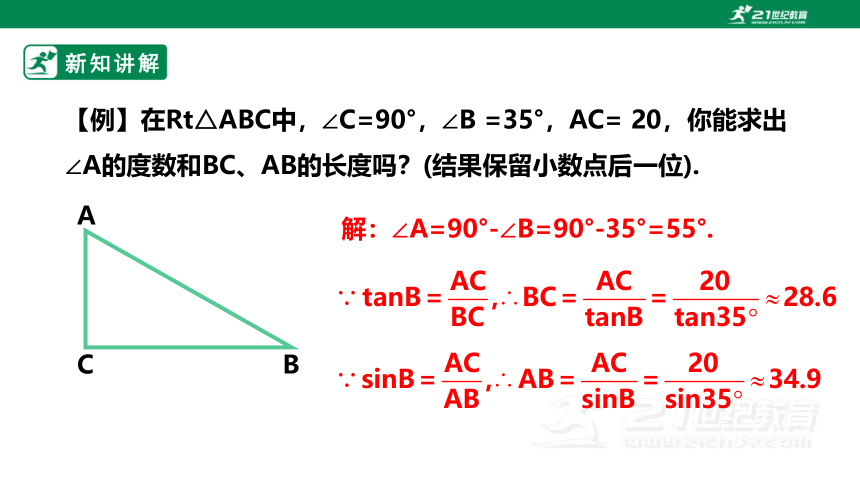
【例】在Rt△ABC中,∠C=90°,∠B =35°,AC= 20,你能求出∠A的度数和BC、AB的长度吗?(结果保留小数点后一位).
A
C
B
解:∠A=90°-∠B=90°-35°=55°.
新知讲解
【归纳】解直角三角形,已知元素可分为下面两种情况:
1.已知两条边;
2.已知一条边和一个锐角(或锐角的某个三角函数).
【注意】多种方法时的选择原则:
①以简便为原则,尽量用乘不用除,减小计算量;
②尽量用原始数据,减小误差.
新知讲解
某些城市规划中,将多层住宅的平屋顶改建成坡屋顶,这样能有效解决顶楼住宅的渗漏、隔热差等问题,并且美化居住景观. 这个改造工程也称为“平改坡”工程.
新知讲解
【例1】下图是某市“平改坡”工程中一种坡屋顶的设计图. 已知原平屋顶的宽度l为10m,坡屋顶高度h为3.5m. 求斜面钢条a的长度和坡角α(长度精确到0.1m,角度精确到1°).
答:斜面钢条a的长度约为6.1m,坡角α约为35°.
新知讲解
【总结归纳】
该例题是用解直角三角形的方法解决简单的实际问题,在直角三角形中,当已知两条边求第三边时,一般选用勾股定理;当已知一条边和一个锐角(或锐角的三角函数)时,选用适当的三角函数求解,解决一个问题往往需要综合运用直角三角形的性质、勾股定理和锐角的三角函数等.
新知讲解
【例2】如图,在Rt△ACB中,∠C=90°,∠A=50°,AB=3.
求∠B和a,b(边长精确到0.1).
解:在Rt△ACB 中,∠B=90°-50°=40°.
新知讲解
【总结归纳】
在解决问题时,要注意分析已知条件,选择合适的求角和边的方法。
(1)当已知一角时采用两锐角互余的方法求另一角比较合理简捷.
(2)在求边长时选用不需要除法运算的三角函数比较便捷.
(3)计算时避免使用近似值代入计算,这样不仅增加计算量,还可能影响结果的准确性.
课堂练习
1.在Rt△ABC中,∠C=90°,AB= ,AC= ,则∠A的度数为( )
A.90°
B.60°
C.45°
D.30°
D
课堂练习
D
课堂练习
C
课堂练习
4.【中考·怀化】在Rt△ABC中,∠C=90°,sin A= ,AC=6 cm,则BC的长度为( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
C
课堂练习
5.在△ABC中,∠B=90°,BC=3,AB=5,求tan A,cos A的值.
课堂练习
6.如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.
若∠A=60°,求BC的长;
课堂总结
本节课你学到了什么?
1.什么是解直角三角形?
2.解直角三角形的知识基础:两锐角互余、勾股定理、锐角三角函数.
3.方法:(1)在直角三角形的六个元素中,除直角外的五个元素,只要知道其中的两个元素(至少有一个是边),就可以求出其余的三个元素.
板书设计
课题:1.3 解直角三角形(1)
教师板演区
学生展示区
一、什么是解直角三角形?
二、怎样解直角三角形?
三、例题讲解
作业布置
课本 P19 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.3 解直角三角形(1)
浙教版九年级下册
教学目标
1.运用锐角三角函数、勾股定理等知识解决在直角三角形中,由已知的一些边、角,求出另一些边角的问题的过程,了解解直角三角形的概念.
2.会运用锐角三角函数、勾股定理等知识解直角三角形,以及解决与直角三角形有关的简单实际问题.
教学重难点
重点:
掌握运用三角函数解直角三角形的方法.
难点:
解直角三角形的过程中,由已知条件求某条边或某个角的方法,以及求这些边、角的顺序往往不唯一,学会如何选择较优的方法和求解顺序。
新知导入
如图,是一个直角三角形,∠C等于90°,你能说一说直角三角形三条边之间的关系吗?
A
C
B
三边之间的关系:直角三角形的两条直角边的平方和等于斜边的平方。
AC2 + BC2 =AB2
直角三角形两个锐角有什么关系?
直角三角形的两个锐角互余:∠A +∠B =90°.
新知导入
直角三角形边和角之间什么关系?
A
C
B
新知讲解
在日常生活和生产实践中,人们经常遇到有关三角形的边长与角度的
计算.
在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做解直角三角形.
新知讲解
【例】在Rt△ABC中,∠C=90°,AC= ,BC= ,你能求出∠A、∠B的度数和AB的长度吗?
A
C
B
∴∠B=90°-∠A=30°.
AB=2AC=
新知讲解
【例】在Rt△ABC中,∠C=90°,∠B =35°,AC= 20,你能求出∠A的度数和BC、AB的长度吗?(结果保留小数点后一位).
A
C
B
解:∠A=90°-∠B=90°-35°=55°.
新知讲解
【归纳】解直角三角形,已知元素可分为下面两种情况:
1.已知两条边;
2.已知一条边和一个锐角(或锐角的某个三角函数).
【注意】多种方法时的选择原则:
①以简便为原则,尽量用乘不用除,减小计算量;
②尽量用原始数据,减小误差.
新知讲解
某些城市规划中,将多层住宅的平屋顶改建成坡屋顶,这样能有效解决顶楼住宅的渗漏、隔热差等问题,并且美化居住景观. 这个改造工程也称为“平改坡”工程.
新知讲解
【例1】下图是某市“平改坡”工程中一种坡屋顶的设计图. 已知原平屋顶的宽度l为10m,坡屋顶高度h为3.5m. 求斜面钢条a的长度和坡角α(长度精确到0.1m,角度精确到1°).
答:斜面钢条a的长度约为6.1m,坡角α约为35°.
新知讲解
【总结归纳】
该例题是用解直角三角形的方法解决简单的实际问题,在直角三角形中,当已知两条边求第三边时,一般选用勾股定理;当已知一条边和一个锐角(或锐角的三角函数)时,选用适当的三角函数求解,解决一个问题往往需要综合运用直角三角形的性质、勾股定理和锐角的三角函数等.
新知讲解
【例2】如图,在Rt△ACB中,∠C=90°,∠A=50°,AB=3.
求∠B和a,b(边长精确到0.1).
解:在Rt△ACB 中,∠B=90°-50°=40°.
新知讲解
【总结归纳】
在解决问题时,要注意分析已知条件,选择合适的求角和边的方法。
(1)当已知一角时采用两锐角互余的方法求另一角比较合理简捷.
(2)在求边长时选用不需要除法运算的三角函数比较便捷.
(3)计算时避免使用近似值代入计算,这样不仅增加计算量,还可能影响结果的准确性.
课堂练习
1.在Rt△ABC中,∠C=90°,AB= ,AC= ,则∠A的度数为( )
A.90°
B.60°
C.45°
D.30°
D
课堂练习
D
课堂练习
C
课堂练习
4.【中考·怀化】在Rt△ABC中,∠C=90°,sin A= ,AC=6 cm,则BC的长度为( )
A.6 cm
B.7 cm
C.8 cm
D.9 cm
C
课堂练习
5.在△ABC中,∠B=90°,BC=3,AB=5,求tan A,cos A的值.
课堂练习
6.如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.
若∠A=60°,求BC的长;
课堂总结
本节课你学到了什么?
1.什么是解直角三角形?
2.解直角三角形的知识基础:两锐角互余、勾股定理、锐角三角函数.
3.方法:(1)在直角三角形的六个元素中,除直角外的五个元素,只要知道其中的两个元素(至少有一个是边),就可以求出其余的三个元素.
板书设计
课题:1.3 解直角三角形(1)
教师板演区
学生展示区
一、什么是解直角三角形?
二、怎样解直角三角形?
三、例题讲解
作业布置
课本 P19 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
