【新课标】1.3 解直角三角形(3) 课件(共26张PPT)
文档属性
| 名称 | 【新课标】1.3 解直角三角形(3) 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-09 00:00:00 | ||
图片预览




文档简介
(共26张PPT)
1.3 解直角三角形(3)
浙教版九年级下册
教学目标
1. 了解方位角、仰角与俯角的概念;
2. 运用解直角三角形来解决方位角问题;
3. 能熟练的应用解直角三角形的知识解决与仰角、俯角有关的实际问题.
教学重难点
重点:
了解方位角、仰角与俯角的概念.
难点:
运用解直角三角形来解决方位角、仰角、俯角有关的实际问题.
新知导入
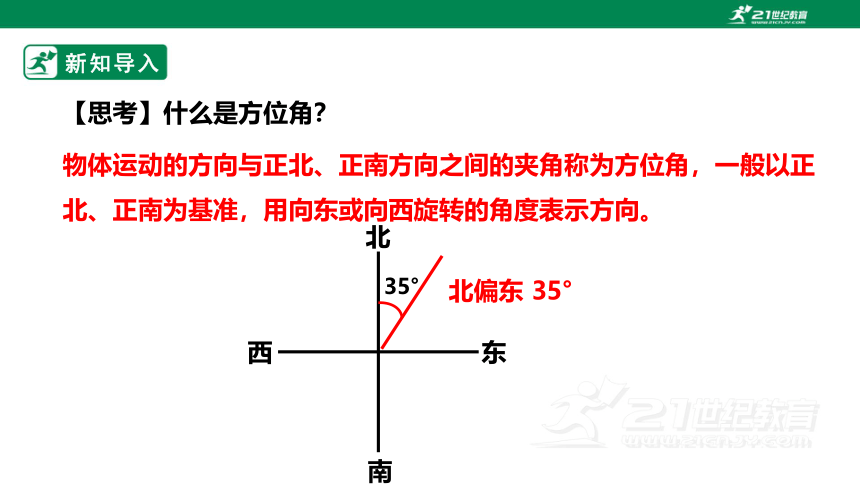
【思考】什么是方位角?
物体运动的方向与正北、正南方向之间的夹角称为方位角,一般以正北、正南为基准,用向东或向西旋转的角度表示方向。
东
西
北
南
35°
北偏东 35°
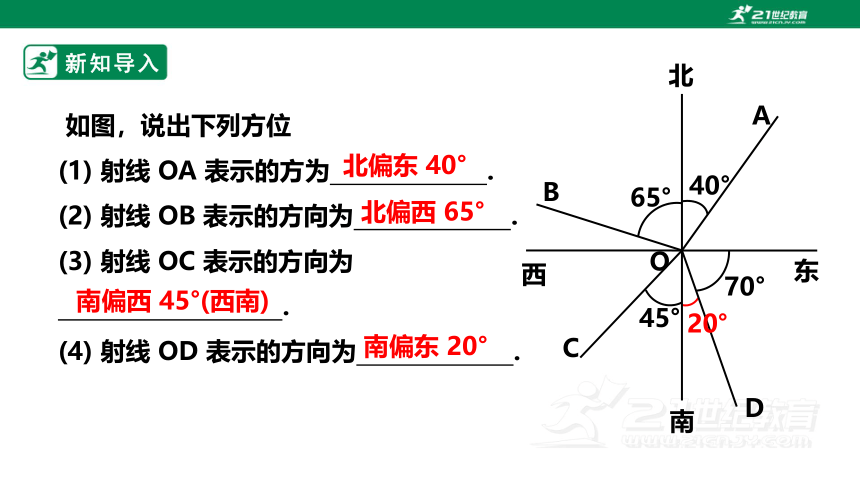
如图,说出下列方位
(1) 射线 OA 表示的方为 .
(2) 射线 OB 表示的方向为 .
(3) 射线 OC 表示的方向为
.
(4) 射线 OD 表示的方向为 .
新知导入
45°
北
东
西
南
C
A
B
D
北偏东 40°
北偏西 65°
南偏西 45°(西南)
南偏东 20°
40°
65°
70°
O
20°
新知讲解
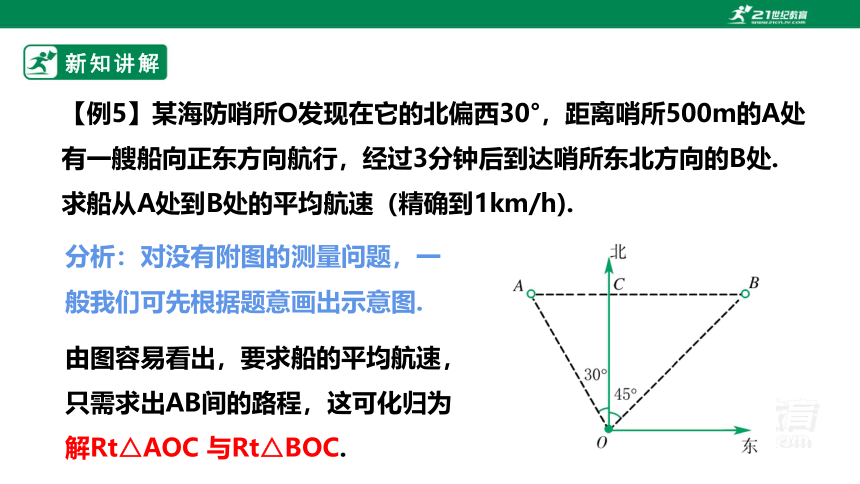
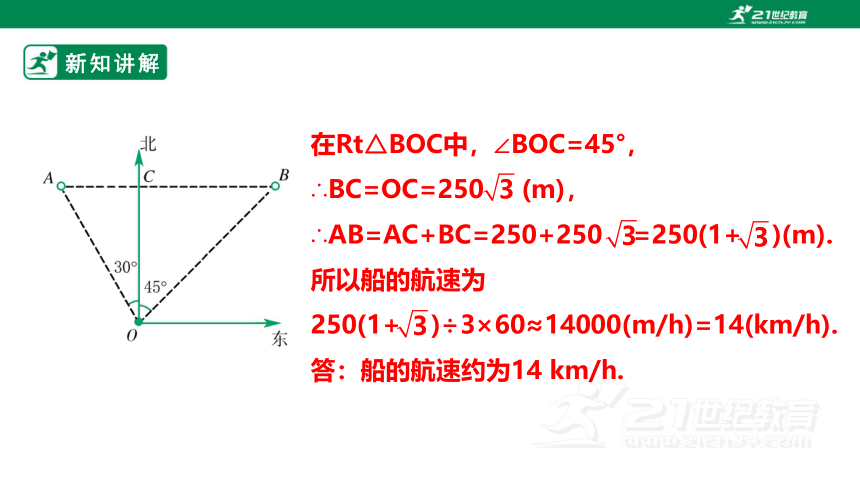
【例5】某海防哨所O发现在它的北偏西30°,距离哨所500m的A处有一艘船向正东方向航行,经过3分钟后到达哨所东北方向的B处.
求船从A处到B处的平均航速(精确到1km/h).
分析:对没有附图的测量问题,一般我们可先根据题意画出示意图.
由图容易看出,要求船的平均航速,只需求出AB间的路程,这可化归为解Rt△AOC 与Rt△BOC.
新知讲解
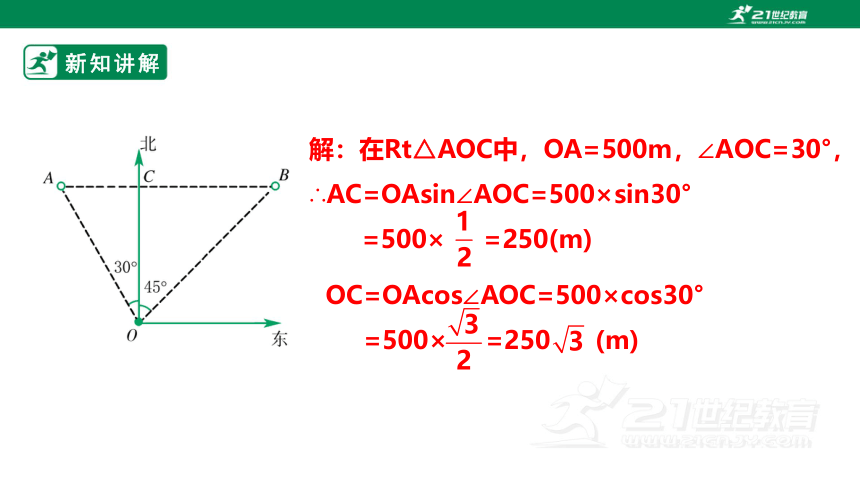
解:在Rt△AOC中,OA=500m,∠AOC=30°,
∴AC=OAsin∠AOC=500×sin30°
=500× =250(m)
OC=OAcos∠AOC=500×cos30°
=500× =250 (m)
新知讲解
在Rt△BOC中,∠BOC=45°,
∴BC=OC=250 (m), ∴AB=AC+BC=250+250 =250(1+ )(m).
所以船的航速为
250(1+ )÷3×60≈14000(m/h)=14(km/h).
答:船的航速约为14 km/h.
新知讲解
在上面的题目中,首先应分析题意,联系速度与时间和路程的关系,已知时间求速度,关键要知道路程,由此将求速度问题转化为求路程问题。然后根据问题的描述画出船的位置和航行路线,借助图形的直观加以分析,用数形结合的方法将实际问题转化为数学中的解直角三角形问题,这是解决上面例题的关键。
【总结归纳】
新知讲解
什么是仰角和俯角?
如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;
从上往下看,视线与水平线下方的夹角叫做俯角.
新知讲解
【例】如图,在量角器的圆心O处下挂一铅锤,制作了一个简易测倾仪.量角器的0°刻度线AB对准楼顶时,铅垂线对应的读数是50°,则此时观察楼顶的仰角度数是( )
A.30° B.40°
C.50° D.60°
B
新知讲解
【例6】如图,测得两楼之间的距离为32.6m,从楼顶点A观测点D的俯角为35°12',点C的俯角为43°24'.求这两幢楼的高度(精确到0.1m).
分析:如图,过D作DE⊥AB,垂足为E. 显然,问题可转化为解Rt△ABC 和Rt△AED.
新知讲解
解:在Rt△ABC中, ∠ACB=∠FAC=43°24', ∴AB=BC·tan∠ACB
=32.6×tan43°24'
≈30.83≈30.8(m).
【例6】如图,测得两楼之间的距离为32.6m,从楼顶点A观测点D的俯角为35°12',点C的俯角为43°24'.求这两幢楼的高度(精确到0.1m).
新知讲解
【例6】如图,测得两楼之间的距离为32.6m,从楼顶点A观测点D的俯角为35°12',点C的俯角为43°24'.求这两幢楼的高度(精确到0.1m).
在Rt△AED中, ∠ADE=∠DAF=35°12', DE=BC=32.6(m),
∴AE=DE·tan∠ADE
=32.6×tan35°12'≈23.00(m).
∴CD=AB-AE≈30.83-23.00
=7.83≈7.8(m).
答:两幢楼高分别约为30.8m和7.8m.
新知讲解
在将实际问题化归为解直角三角形问题中,构造适当的直角三角形是关键。航行问题中的三角形往往由方位线和航行路线构成,高度测量问题中的三角形由视线、水平线和铅垂线等构成。方位线、视线可分别由方位角和视角确定,这就要求我们对方位角、和各种视角(如仰角、俯角、观察角)有准确的理解和想象,并准确画出这些线.
【总结归纳】
课堂练习
D
课堂练习
B
课堂练习
3.如图,一轮船在M处观测灯塔P位于南偏西30°方向,该轮船沿正南方向以15海里/小时的速度匀速航行2小时后到达N处,再观测灯塔P位于南偏西60°方向.若该轮船继续向南航行至离灯塔P最近的位置T处,此时轮船与灯塔之间的距离PT为________海里.(结果保留根号)
课堂练习
C
课堂练习
5.如图,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点D处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上,已知CD=9.6 m,则旗杆AB的高度为________m.
14.4
课堂练习
6.如图,某建筑物BC上有一旗杆AB,某人站在与BC相距38 m的D处观测到旗杆顶部A的仰角为50°,观测到旗杆底部B的仰角为45°,则旗杆的高度约为________.(结果精确到0.1 m.参考数据:sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.19)
7.2 m
课堂总结
本节课你学到了什么?
1.运用解直角三角形解决方位角问题.
2.仰角、俯角的概念.
3.运用解直角三角形解决仰角、俯角问题.
板书设计
课题:1.3 解直角三角形(3)
教师板演区
学生展示区
一、方位角
二、仰角和俯角
三、解决实际问题
作业布置
课本 P25 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.3 解直角三角形(3)
浙教版九年级下册
教学目标
1. 了解方位角、仰角与俯角的概念;
2. 运用解直角三角形来解决方位角问题;
3. 能熟练的应用解直角三角形的知识解决与仰角、俯角有关的实际问题.
教学重难点
重点:
了解方位角、仰角与俯角的概念.
难点:
运用解直角三角形来解决方位角、仰角、俯角有关的实际问题.
新知导入
【思考】什么是方位角?
物体运动的方向与正北、正南方向之间的夹角称为方位角,一般以正北、正南为基准,用向东或向西旋转的角度表示方向。
东
西
北
南
35°
北偏东 35°
如图,说出下列方位
(1) 射线 OA 表示的方为 .
(2) 射线 OB 表示的方向为 .
(3) 射线 OC 表示的方向为
.
(4) 射线 OD 表示的方向为 .
新知导入
45°
北
东
西
南
C
A
B
D
北偏东 40°
北偏西 65°
南偏西 45°(西南)
南偏东 20°
40°
65°
70°
O
20°
新知讲解
【例5】某海防哨所O发现在它的北偏西30°,距离哨所500m的A处有一艘船向正东方向航行,经过3分钟后到达哨所东北方向的B处.
求船从A处到B处的平均航速(精确到1km/h).
分析:对没有附图的测量问题,一般我们可先根据题意画出示意图.
由图容易看出,要求船的平均航速,只需求出AB间的路程,这可化归为解Rt△AOC 与Rt△BOC.
新知讲解
解:在Rt△AOC中,OA=500m,∠AOC=30°,
∴AC=OAsin∠AOC=500×sin30°
=500× =250(m)
OC=OAcos∠AOC=500×cos30°
=500× =250 (m)
新知讲解
在Rt△BOC中,∠BOC=45°,
∴BC=OC=250 (m), ∴AB=AC+BC=250+250 =250(1+ )(m).
所以船的航速为
250(1+ )÷3×60≈14000(m/h)=14(km/h).
答:船的航速约为14 km/h.
新知讲解
在上面的题目中,首先应分析题意,联系速度与时间和路程的关系,已知时间求速度,关键要知道路程,由此将求速度问题转化为求路程问题。然后根据问题的描述画出船的位置和航行路线,借助图形的直观加以分析,用数形结合的方法将实际问题转化为数学中的解直角三角形问题,这是解决上面例题的关键。
【总结归纳】
新知讲解
什么是仰角和俯角?
如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;
从上往下看,视线与水平线下方的夹角叫做俯角.
新知讲解
【例】如图,在量角器的圆心O处下挂一铅锤,制作了一个简易测倾仪.量角器的0°刻度线AB对准楼顶时,铅垂线对应的读数是50°,则此时观察楼顶的仰角度数是( )
A.30° B.40°
C.50° D.60°
B
新知讲解
【例6】如图,测得两楼之间的距离为32.6m,从楼顶点A观测点D的俯角为35°12',点C的俯角为43°24'.求这两幢楼的高度(精确到0.1m).
分析:如图,过D作DE⊥AB,垂足为E. 显然,问题可转化为解Rt△ABC 和Rt△AED.
新知讲解
解:在Rt△ABC中, ∠ACB=∠FAC=43°24', ∴AB=BC·tan∠ACB
=32.6×tan43°24'
≈30.83≈30.8(m).
【例6】如图,测得两楼之间的距离为32.6m,从楼顶点A观测点D的俯角为35°12',点C的俯角为43°24'.求这两幢楼的高度(精确到0.1m).
新知讲解
【例6】如图,测得两楼之间的距离为32.6m,从楼顶点A观测点D的俯角为35°12',点C的俯角为43°24'.求这两幢楼的高度(精确到0.1m).
在Rt△AED中, ∠ADE=∠DAF=35°12', DE=BC=32.6(m),
∴AE=DE·tan∠ADE
=32.6×tan35°12'≈23.00(m).
∴CD=AB-AE≈30.83-23.00
=7.83≈7.8(m).
答:两幢楼高分别约为30.8m和7.8m.
新知讲解
在将实际问题化归为解直角三角形问题中,构造适当的直角三角形是关键。航行问题中的三角形往往由方位线和航行路线构成,高度测量问题中的三角形由视线、水平线和铅垂线等构成。方位线、视线可分别由方位角和视角确定,这就要求我们对方位角、和各种视角(如仰角、俯角、观察角)有准确的理解和想象,并准确画出这些线.
【总结归纳】
课堂练习
D
课堂练习
B
课堂练习
3.如图,一轮船在M处观测灯塔P位于南偏西30°方向,该轮船沿正南方向以15海里/小时的速度匀速航行2小时后到达N处,再观测灯塔P位于南偏西60°方向.若该轮船继续向南航行至离灯塔P最近的位置T处,此时轮船与灯塔之间的距离PT为________海里.(结果保留根号)
课堂练习
C
课堂练习
5.如图,为测量旗杆AB的高度,在教学楼一楼点C处测得旗杆顶部的仰角为60°,在四楼点D处测得旗杆顶部的仰角为30°,点C与点B在同一水平线上,已知CD=9.6 m,则旗杆AB的高度为________m.
14.4
课堂练习
6.如图,某建筑物BC上有一旗杆AB,某人站在与BC相距38 m的D处观测到旗杆顶部A的仰角为50°,观测到旗杆底部B的仰角为45°,则旗杆的高度约为________.(结果精确到0.1 m.参考数据:sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.19)
7.2 m
课堂总结
本节课你学到了什么?
1.运用解直角三角形解决方位角问题.
2.仰角、俯角的概念.
3.运用解直角三角形解决仰角、俯角问题.
板书设计
课题:1.3 解直角三角形(3)
教师板演区
学生展示区
一、方位角
二、仰角和俯角
三、解决实际问题
作业布置
课本 P25 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
