锐角三角函数 课件
图片预览








文档简介
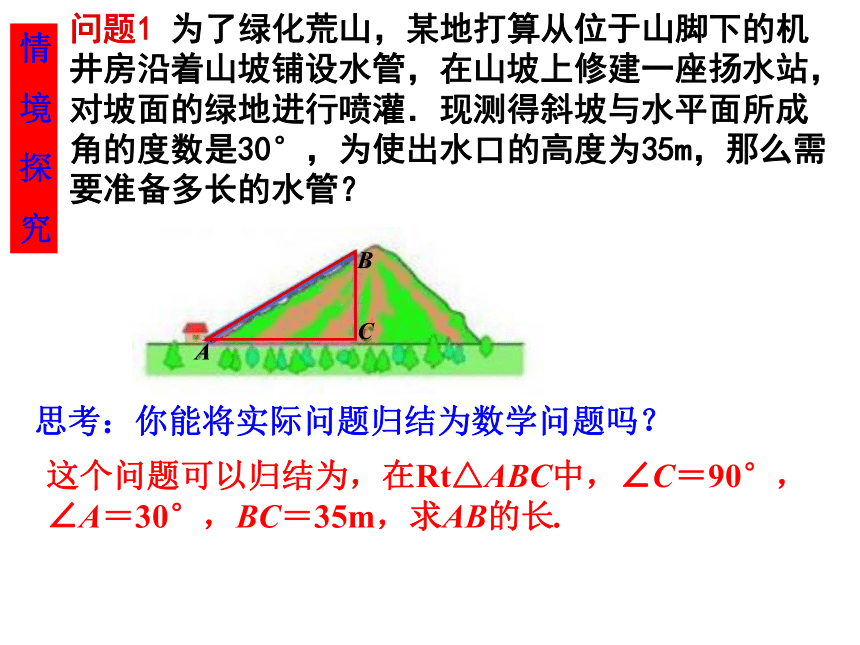
课件55张PPT。28.1锐角三角函数(一)——正弦 、余弦 、正切问题1 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?这个问题可以归结为,在Rt△ABC中,∠C=90°,∠A=30°,BC=35m,求AB的长. 思考:你能将实际问题归结为数学问题吗?情
境
探
究 在Rt△ABC中,∠C=90°,∠A=30°,BC= 35m,求AB的长.所以 AB=2BC=70m,即需要准备70m长的水管。结论:在Rt△ABC中,∠C=90°,
∠A=30°,解:在Rt△ABC中,∠C=90°,
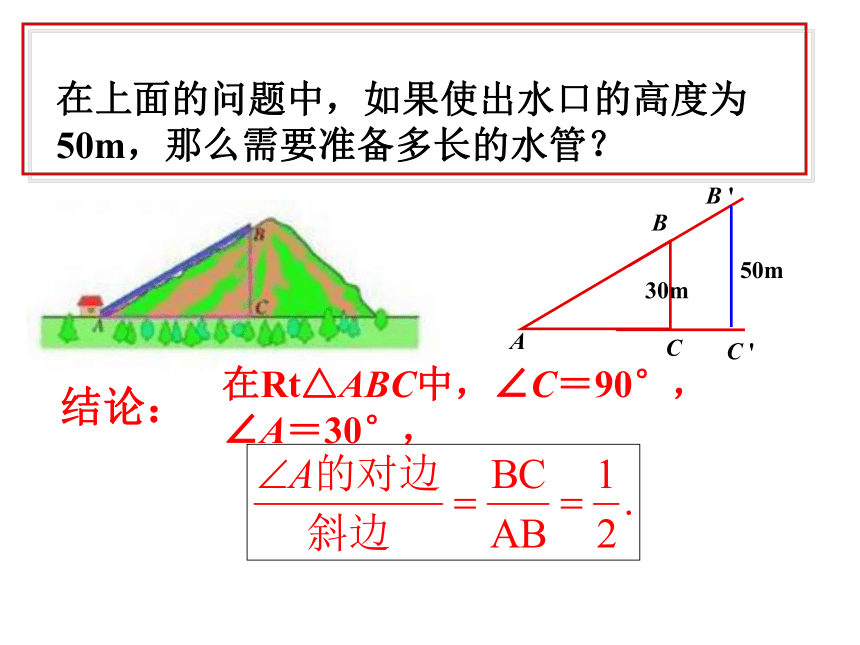
∠A=30°,在上面的问题中,如果使出水口的高度为50m,那么需要准备多长的水管?ABC50m30mB 'C '结论:在Rt△ABC中,∠C=90°,
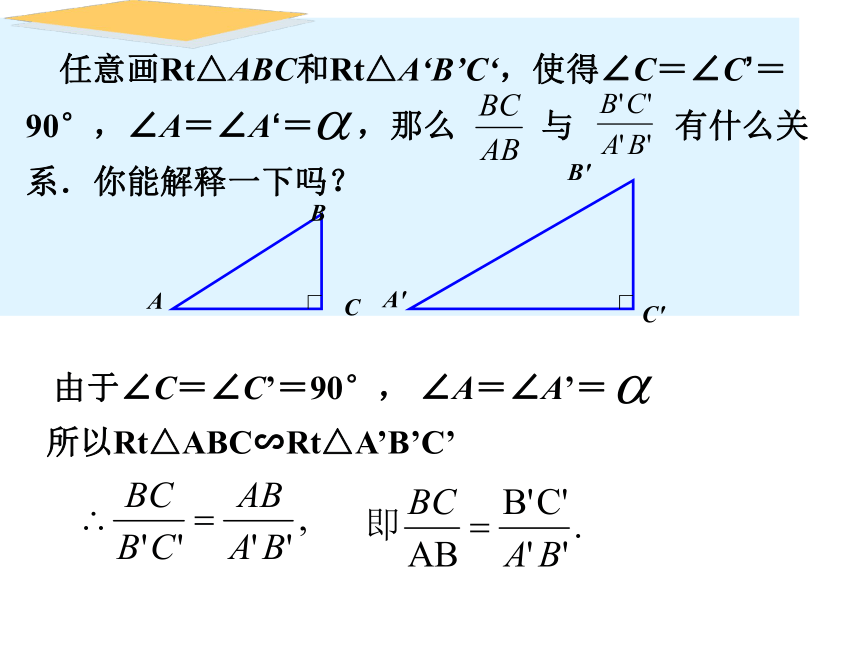
∠A=30°, 即在直角三角形中,当一个锐角等于45°时,不管这个直角三角形的大小如何,这个角的对边与斜边的比都等于 。 如图,任意画一个Rt△ABC,使∠C=90°,∠A=45°,计算∠A的对边与斜边的比 ,你能得出什么结论?ABC 综上可知,在一个Rt△ABC中,∠C=90°, 一般地,在一个Rt△ABC中,∠C=90°当∠A 取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值?问题 当∠A=30°时,∠A的对边与斜边的比都等于 ,是一个固定值; 当∠A=45°时,∠A的对边与斜边的比都等于 ,也是一个固定值.ABCA'B'C' 任意画Rt△ABC和Rt△A‘B’C‘,使得∠C=∠C’=90°,∠A=∠A‘= ,那么 与 有什么关系.你能解释一下吗?由于∠C=∠C’=90°, ∠A=∠A’= 所以Rt△ABC∽Rt△A’B’C’ 这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比都是一个固定值.探究 如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA, 即例如,当∠A=30°时,我们有当∠A=45°时,我们有cab对边斜边注意sinA是一个完整的符号,它表示∠A的正弦,记号里习惯省去角的符号“∠”;
sinA没有单位,它表示一个比值,即直角三角形中∠A的对边与斜边的比;
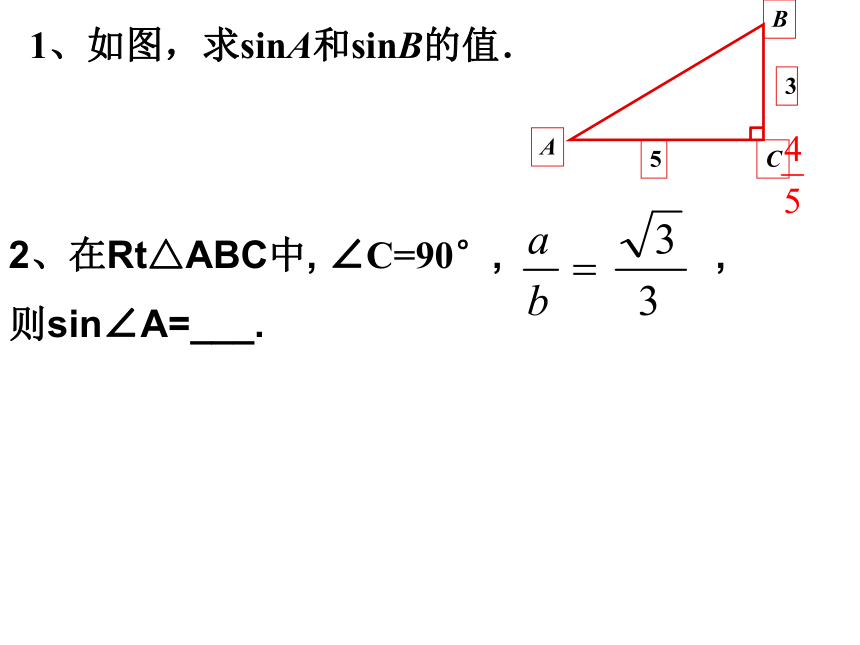
sinA不表示“sin”乘以“A”。例1 如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.ABC34(1)(2)试着完成图(2)2、在Rt△ABC中, ∠C=90°, ,
则sin∠A=___.1、如图,求sinA和sinB的值.3、如图,在△ABC中, AB=CB=5,sinA= ,求△ABC 的面积。1.锐角正弦的定义 在 中, ∠A的正弦:2、当锐角A确定时,∠A的对边与斜边的比就随之确定。此时,其他边之间的比是否也随之确定?为什么?新知探索:1、你能将“其他边之比”用比例的式子表示出来吗?这样的比有多少?2、当锐角A确定时,∠A的邻边与斜边的比, ∠A的对边与邻边的比也随之确定吗?为什么?交流并说出理由。 如图,在Rt△ABC中,∠C=90°:锐角A的邻边与斜边的比叫做∠A的
余弦(cosine),记作cosA, 即锐角A的对边与邻边的比叫做∠A的
正切(tangent),记作tanA, 即注意cosA,tanA是一个完整的符号,它表示∠A的余弦、正切,记号里习惯省去角的符号“∠”;
cosA,tanA没有单位,它表示一个比值,即直角三角形中∠A的邻边与斜边的比、对边与邻边的比;
cosA不表示“cos”乘以“A”, tanA不表示“tan”乘以“A”例2 如图,在Rt△ABC中,∠C=90°,BC=2,AB=3,求∠A,∠B的正弦、余弦、正切值.延伸:由上面的计算,你能猜想∠A,∠B的正弦、余弦值有什么规律吗?结论:一个锐角的正弦等于它余角的余弦,或一个锐角的余弦等于它余角的正弦。例3 如图,在Rt△ABC中,∠C=90°,BC=6, ,求cosA和tanB的值.28.1锐角三角函数(二)——正弦 、余弦 、正切 锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数. 如图,在Rt△ABC中,∠C=90°,cosA= ,求
sinA、tanA的值.解:在Rt△ABC中,∠C=90°
∵设AC=15k,则AB=17k所以 如图,在Rt△ABC中,∠C=90°1.求证:sinA=cosB,sinB=cosA2.求证:3.求证: 在Rt△ABC中,如果各边长都扩大2倍,那么锐角A的正弦值、余弦值和正切值有什么变化?解:在Rt△ABC中,∠C=90°
设各边长分别为a、b、c,∠A的三个三角函数分别为则扩大2倍后三边分别为2a、2b、2c如图,Rt△ABC中, ∠C=90度,因为0<sinA <1, 0<sinB <1, tan A>0, tan B>0 0<cosA <1, 0<cosB <1,所以,对于任何一个锐角α ,有
0<sin α <1,
0<cos α <1,
tan α >0,练习
1、在等腰△ABC中,AB=AC=5,BC=6,求sinB,cosB,tanB.D补充练习2、如图所示,在△ABC中,∠ACB=90°,AC=12,AB=13,∠BCM=∠BAC,求sin∠BAC和点B到直线MC的距离.
3、如图所示,CD是Rt△ABC的斜边AB上的高,
求证:28.1锐角三角函数(3) AB C∠A的对边a∠A的邻边b斜边c 请同学们拿出自己的学习工具——一副三角尺,思考并回答下列问题:1、这两块三角尺各有几个锐角?它们分别等于多少度?2、每块三角尺的三边之间有怎样的特殊关系?如果设每块三角尺较短的边长为1,请你说出未知边的长度。30°60°45°121145°新知探索:30°角的三角函数值sin30°=cos30°=tan30°=cos45°=tan45°=sin45°=新知探索:45°角的三角函数值sin60°=cos60°=tan60°=新知探索:60°角的三角函数值30°、45°、60°角的正弦值、余弦值和正切值如下表:例1 求下列各式的值:
(1)cos260°+sin260°
(2)
1.求下列各式的值:2、求适合下列各式的锐角α例2 (1)如图,在Rt△ABC中,∠C=90°, ,
求∠A的度数.(2)如图,已知圆锥的高AO等于圆锥的底面半径OB的 倍,求 a . 当A,B为锐角
时,若A≠B,则
sinA≠sinB,
cosA≠cosB,
tanA≠tanB. 1、在Rt△ABC中,∠C=90°,
,
求∠A、∠B的度数.BACABCD4、如图,△ABC中,∠C=900,BD平分∠ABC,
BC=12,BD= ,求∠A的度数及AD的长.小结 : 我们学习了30°, 45°, 60°这几类特殊角的三角函数值. 作业课本P82 第3题
《同步练习》P51-52(四)(五)28.1锐角三角函数(4) 引例 升国旗时,小明站在操场上离国旗20m处行注目礼。当国旗升至顶端时,小明看国旗视线的仰角为42°(如图所示),若小明双眼离地面1.60m,你能帮助小明求出旗杆AB的高度吗?这里的tan42°是多少呢? 前面我们学习了特殊角30°45°60°的三角函数值,一些非特殊角(如17°56°89°等)的三角函数值又怎么求呢? 这一节课我们就学习借助计算器来完成这个任务.rldmm89898891、用科学计算器求一般锐角的三角函数值:(1)我们要用到科学计算器中的键:sincostan(2)按键顺序◆如果锐角恰是整数度数时,以“求sin18°”为例,按键顺序如下:sin18sin180.309 016 994∴ sin18°= 0.309 016 994≈0.311、用科学计算器求一般锐角的三角函数值:◆如果锐角的度数是度、分形式时,以“求tan30°36′”为例,按键顺序如下:方法一:tan3036tan30°36′0.591 398 351∴ tan30°36′ = 0.591 398 351≈0.59方法二:先转化, 30°36′ =30.6°,后仿照 sin18°的求法。◆如果锐角的度数是度、分、秒形式时,依照上面的方法一求解。(3)完成引例中的求解:tan2042+1.619.608 080 89∴ AB = 19.608 080 89≈19.61m即旗杆的高度是19.61m.练习:使用计算器求下列锐角的三角函数值.(精确到0.01)(1)sin20°,cos70°;
sin35°,cos55°;
sin15°32′,cos74°28′;(2)tan3°8′,tan80°25′43″;(3)sin15°+cos61°tan76°.SHIFT20917.301507834sin·7= 已知三角函数值求角度,要用到sin,Cos,tan的第二功能键“sin-1 Cos-1,tan-1”键例如:已知sinα=0.2974,求锐角α.按健顺序为:如果再按“度分秒健”就换算成度分秒,°′″即∠ α=17o18’5.43”2、已知锐角的三角函数值,求锐角的度数:例 根据下面的条件,求锐角β的大小(精确到1″)
(1)sinβ=0.4511;(2)cosβ=0.7857;
(3) tanβ=1.4036.
按键盘顺序如下:26048’51”0.sin115=4SHIFT°′″即∠ β =26048’51”驶向胜利的彼岸练习:1、已知下列锐角三角函数值,用计算器求其相应的锐角:(1)sinA=0.627 5,sinB=0.054 7;
(2)cosA=0.625 2,cosB=0.165 9;
(3)tanA=4.842 5,tanB=0.881 6.2、已知tanA=3.1748,利用计算器求锐角A的度数。(精确到1′)答案:∠A≈72°52′练习:3、已知锐角a的三角函数值,使用计算器求锐角a(精确到1′)
(1)sin a=0.2476;(2)cos a=0.4;(3)tan a=0.1890. 答案: (1)α≈14°20′;(3)α≈10°42′.(2)α≈65°20′;ABOR
境
探
究 在Rt△ABC中,∠C=90°,∠A=30°,BC= 35m,求AB的长.所以 AB=2BC=70m,即需要准备70m长的水管。结论:在Rt△ABC中,∠C=90°,
∠A=30°,解:在Rt△ABC中,∠C=90°,
∠A=30°,在上面的问题中,如果使出水口的高度为50m,那么需要准备多长的水管?ABC50m30mB 'C '结论:在Rt△ABC中,∠C=90°,
∠A=30°, 即在直角三角形中,当一个锐角等于45°时,不管这个直角三角形的大小如何,这个角的对边与斜边的比都等于 。 如图,任意画一个Rt△ABC,使∠C=90°,∠A=45°,计算∠A的对边与斜边的比 ,你能得出什么结论?ABC 综上可知,在一个Rt△ABC中,∠C=90°, 一般地,在一个Rt△ABC中,∠C=90°当∠A 取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值?问题 当∠A=30°时,∠A的对边与斜边的比都等于 ,是一个固定值; 当∠A=45°时,∠A的对边与斜边的比都等于 ,也是一个固定值.ABCA'B'C' 任意画Rt△ABC和Rt△A‘B’C‘,使得∠C=∠C’=90°,∠A=∠A‘= ,那么 与 有什么关系.你能解释一下吗?由于∠C=∠C’=90°, ∠A=∠A’= 所以Rt△ABC∽Rt△A’B’C’ 这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比都是一个固定值.探究 如图,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA, 即例如,当∠A=30°时,我们有当∠A=45°时,我们有cab对边斜边注意sinA是一个完整的符号,它表示∠A的正弦,记号里习惯省去角的符号“∠”;
sinA没有单位,它表示一个比值,即直角三角形中∠A的对边与斜边的比;
sinA不表示“sin”乘以“A”。例1 如图,在Rt△ABC中,∠C=90°,求sinA和sinB的值.ABC34(1)(2)试着完成图(2)2、在Rt△ABC中, ∠C=90°, ,
则sin∠A=___.1、如图,求sinA和sinB的值.3、如图,在△ABC中, AB=CB=5,sinA= ,求△ABC 的面积。1.锐角正弦的定义 在 中, ∠A的正弦:2、当锐角A确定时,∠A的对边与斜边的比就随之确定。此时,其他边之间的比是否也随之确定?为什么?新知探索:1、你能将“其他边之比”用比例的式子表示出来吗?这样的比有多少?2、当锐角A确定时,∠A的邻边与斜边的比, ∠A的对边与邻边的比也随之确定吗?为什么?交流并说出理由。 如图,在Rt△ABC中,∠C=90°:锐角A的邻边与斜边的比叫做∠A的
余弦(cosine),记作cosA, 即锐角A的对边与邻边的比叫做∠A的
正切(tangent),记作tanA, 即注意cosA,tanA是一个完整的符号,它表示∠A的余弦、正切,记号里习惯省去角的符号“∠”;
cosA,tanA没有单位,它表示一个比值,即直角三角形中∠A的邻边与斜边的比、对边与邻边的比;
cosA不表示“cos”乘以“A”, tanA不表示“tan”乘以“A”例2 如图,在Rt△ABC中,∠C=90°,BC=2,AB=3,求∠A,∠B的正弦、余弦、正切值.延伸:由上面的计算,你能猜想∠A,∠B的正弦、余弦值有什么规律吗?结论:一个锐角的正弦等于它余角的余弦,或一个锐角的余弦等于它余角的正弦。例3 如图,在Rt△ABC中,∠C=90°,BC=6, ,求cosA和tanB的值.28.1锐角三角函数(二)——正弦 、余弦 、正切 锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数. 如图,在Rt△ABC中,∠C=90°,cosA= ,求
sinA、tanA的值.解:在Rt△ABC中,∠C=90°
∵设AC=15k,则AB=17k所以 如图,在Rt△ABC中,∠C=90°1.求证:sinA=cosB,sinB=cosA2.求证:3.求证: 在Rt△ABC中,如果各边长都扩大2倍,那么锐角A的正弦值、余弦值和正切值有什么变化?解:在Rt△ABC中,∠C=90°
设各边长分别为a、b、c,∠A的三个三角函数分别为则扩大2倍后三边分别为2a、2b、2c如图,Rt△ABC中, ∠C=90度,因为0<sinA <1, 0<sinB <1, tan A>0, tan B>0 0<cosA <1, 0<cosB <1,所以,对于任何一个锐角α ,有
0<sin α <1,
0<cos α <1,
tan α >0,练习
1、在等腰△ABC中,AB=AC=5,BC=6,求sinB,cosB,tanB.D补充练习2、如图所示,在△ABC中,∠ACB=90°,AC=12,AB=13,∠BCM=∠BAC,求sin∠BAC和点B到直线MC的距离.
3、如图所示,CD是Rt△ABC的斜边AB上的高,
求证:28.1锐角三角函数(3) AB C∠A的对边a∠A的邻边b斜边c 请同学们拿出自己的学习工具——一副三角尺,思考并回答下列问题:1、这两块三角尺各有几个锐角?它们分别等于多少度?2、每块三角尺的三边之间有怎样的特殊关系?如果设每块三角尺较短的边长为1,请你说出未知边的长度。30°60°45°121145°新知探索:30°角的三角函数值sin30°=cos30°=tan30°=cos45°=tan45°=sin45°=新知探索:45°角的三角函数值sin60°=cos60°=tan60°=新知探索:60°角的三角函数值30°、45°、60°角的正弦值、余弦值和正切值如下表:例1 求下列各式的值:
(1)cos260°+sin260°
(2)
1.求下列各式的值:2、求适合下列各式的锐角α例2 (1)如图,在Rt△ABC中,∠C=90°, ,
求∠A的度数.(2)如图,已知圆锥的高AO等于圆锥的底面半径OB的 倍,求 a . 当A,B为锐角
时,若A≠B,则
sinA≠sinB,
cosA≠cosB,
tanA≠tanB. 1、在Rt△ABC中,∠C=90°,
,
求∠A、∠B的度数.BACABCD4、如图,△ABC中,∠C=900,BD平分∠ABC,
BC=12,BD= ,求∠A的度数及AD的长.小结 : 我们学习了30°, 45°, 60°这几类特殊角的三角函数值. 作业课本P82 第3题
《同步练习》P51-52(四)(五)28.1锐角三角函数(4) 引例 升国旗时,小明站在操场上离国旗20m处行注目礼。当国旗升至顶端时,小明看国旗视线的仰角为42°(如图所示),若小明双眼离地面1.60m,你能帮助小明求出旗杆AB的高度吗?这里的tan42°是多少呢? 前面我们学习了特殊角30°45°60°的三角函数值,一些非特殊角(如17°56°89°等)的三角函数值又怎么求呢? 这一节课我们就学习借助计算器来完成这个任务.rldmm89898891、用科学计算器求一般锐角的三角函数值:(1)我们要用到科学计算器中的键:sincostan(2)按键顺序◆如果锐角恰是整数度数时,以“求sin18°”为例,按键顺序如下:sin18sin180.309 016 994∴ sin18°= 0.309 016 994≈0.311、用科学计算器求一般锐角的三角函数值:◆如果锐角的度数是度、分形式时,以“求tan30°36′”为例,按键顺序如下:方法一:tan3036tan30°36′0.591 398 351∴ tan30°36′ = 0.591 398 351≈0.59方法二:先转化, 30°36′ =30.6°,后仿照 sin18°的求法。◆如果锐角的度数是度、分、秒形式时,依照上面的方法一求解。(3)完成引例中的求解:tan2042+1.619.608 080 89∴ AB = 19.608 080 89≈19.61m即旗杆的高度是19.61m.练习:使用计算器求下列锐角的三角函数值.(精确到0.01)(1)sin20°,cos70°;
sin35°,cos55°;
sin15°32′,cos74°28′;(2)tan3°8′,tan80°25′43″;(3)sin15°+cos61°tan76°.SHIFT20917.301507834sin·7= 已知三角函数值求角度,要用到sin,Cos,tan的第二功能键“sin-1 Cos-1,tan-1”键例如:已知sinα=0.2974,求锐角α.按健顺序为:如果再按“度分秒健”就换算成度分秒,°′″即∠ α=17o18’5.43”2、已知锐角的三角函数值,求锐角的度数:例 根据下面的条件,求锐角β的大小(精确到1″)
(1)sinβ=0.4511;(2)cosβ=0.7857;
(3) tanβ=1.4036.
按键盘顺序如下:26048’51”0.sin115=4SHIFT°′″即∠ β =26048’51”驶向胜利的彼岸练习:1、已知下列锐角三角函数值,用计算器求其相应的锐角:(1)sinA=0.627 5,sinB=0.054 7;
(2)cosA=0.625 2,cosB=0.165 9;
(3)tanA=4.842 5,tanB=0.881 6.2、已知tanA=3.1748,利用计算器求锐角A的度数。(精确到1′)答案:∠A≈72°52′练习:3、已知锐角a的三角函数值,使用计算器求锐角a(精确到1′)
(1)sin a=0.2476;(2)cos a=0.4;(3)tan a=0.1890. 答案: (1)α≈14°20′;(3)α≈10°42′.(2)α≈65°20′;ABOR
