1.3解直角三角形第一课时 课件(共15张PPT)
文档属性
| 名称 | 1.3解直角三角形第一课时 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
1.3 解直角三角形
第一课时
浙教版九年级下册
教学目标
1.了解解直角三角形的概念
2.会解以下情形的直角三角形
(1)已知两边解直角三角形
(2)已知一边及一锐角解直角三角形
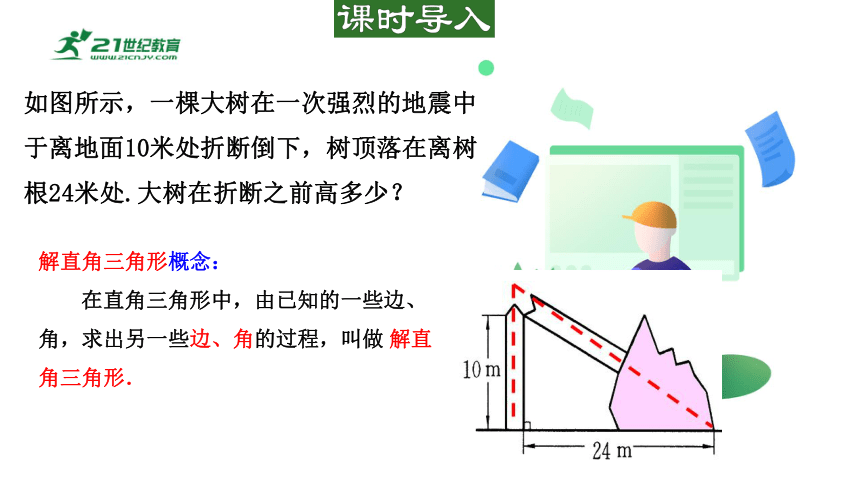
如图所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
解直角三角形概念:
在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做 解直角三角形.
1
知识点
已知两边解直角三角形
问:在三角形中共有几个元素?
1.三个角,三条边,共六个元素。
问:直角三角形ABC中,∠ C=90°,a、b、c 、∠A、∠B这五个元素间有哪些等量关系呢?
课堂总结
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
∠A+∠B=900
a2+b2=c2
C
A
B
斜边
的对边
正弦函数:
A
A
∠
=
sin
的邻边
的对边
正切函数:
A
A
A
∠
∠
=
tan
斜边
的邻边
余弦函数:
A
A
∠
=
cos
例1 在Rt△ABC中,∠C=90°,c=2 ,a=3,解这个直角三角形.
方法小结:已知斜边和一条直角边的长,
①先利用勾股定理求出另一条直角边的长
②再利用正弦或余弦求角的度数.
课堂练习
1.在Rt△ABC中,∠C=90°
(1)若c= a=6,则b=____,∠B=____, ∠A=_____;
(2)若a= b=4,则∠A=__,∠B= ,c=________.
2.在△ABC中,∠C=90°,AB=4,AC=3,欲求∠A的值,
最适宜的做法是( )
A.计算tanA的值求出
B.计算sinA的值求出
C.计算cosA的值求出
D.先根据sinB求出∠B,再利用90°-∠B求出
拓 展
解直角三角形时,选择函数关系式遵循的基本原则: “有斜(斜边)用弦(正弦、余弦),无斜用切(正切);宁乘勿除,取原避中”.
选择关系式时要尽量利用已知条件,解直角三角形时必须求出所有的未知元素.
例题
2
知识点
已知一边及一锐角解直角三角形
如图 ,在Rt△ABC中,∠C=90°,∠A=50。,AB=3.
求∠B和a,b(边长精确到0.1).
参考数据:sin 50。≈0.766,cos 50。≈0.643, tan50。≈1.192
课堂总结
已知斜边c和一锐角∠A,解直角三角形的一般步骤是:
(1)根据∠A+∠B=90°求出∠B;
(2)根据sin A= ,求出a;
(3)根据cos A= ,求出b或根据勾股定理求出b.
课堂练习
在Rt△ABC中,∠C=90°.
(1)若∠B=60°, BC= 则∠A=_______,
AC=________, AB=________;
(2)若∠A=45°,AB=2,则∠B=________,
AC= ________,BC=________.
在Rt△ABC中,∠C=90°,∠B=37°, BC=32,则AC=_.
(参考数据: sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
作业布置
1.教材P9 作业题1,3
2.作业本1.3解直角三角形(1)
的边角关系
直角三角形
解直角三角形
解直角三角形
实际应用
知一边一锐角
解直角三角形
知两边解直角三角形
添设辅助线解直角三角形
知斜边一锐角解直角三角形
知一直角边一锐角解直角三角形
知两直角边解直角三角形
知一斜边一直角解直角三角形
直接抽象出直角三角形
抽象出图形,再添设辅助线求解
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.3 解直角三角形
第一课时
浙教版九年级下册
教学目标
1.了解解直角三角形的概念
2.会解以下情形的直角三角形
(1)已知两边解直角三角形
(2)已知一边及一锐角解直角三角形
如图所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?
解直角三角形概念:
在直角三角形中,由已知的一些边、角,求出另一些边、角的过程,叫做 解直角三角形.
1
知识点
已知两边解直角三角形
问:在三角形中共有几个元素?
1.三个角,三条边,共六个元素。
问:直角三角形ABC中,∠ C=90°,a、b、c 、∠A、∠B这五个元素间有哪些等量关系呢?
课堂总结
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
∠A+∠B=900
a2+b2=c2
C
A
B
斜边
的对边
正弦函数:
A
A
∠
=
sin
的邻边
的对边
正切函数:
A
A
A
∠
∠
=
tan
斜边
的邻边
余弦函数:
A
A
∠
=
cos
例1 在Rt△ABC中,∠C=90°,c=2 ,a=3,解这个直角三角形.
方法小结:已知斜边和一条直角边的长,
①先利用勾股定理求出另一条直角边的长
②再利用正弦或余弦求角的度数.
课堂练习
1.在Rt△ABC中,∠C=90°
(1)若c= a=6,则b=____,∠B=____, ∠A=_____;
(2)若a= b=4,则∠A=__,∠B= ,c=________.
2.在△ABC中,∠C=90°,AB=4,AC=3,欲求∠A的值,
最适宜的做法是( )
A.计算tanA的值求出
B.计算sinA的值求出
C.计算cosA的值求出
D.先根据sinB求出∠B,再利用90°-∠B求出
拓 展
解直角三角形时,选择函数关系式遵循的基本原则: “有斜(斜边)用弦(正弦、余弦),无斜用切(正切);宁乘勿除,取原避中”.
选择关系式时要尽量利用已知条件,解直角三角形时必须求出所有的未知元素.
例题
2
知识点
已知一边及一锐角解直角三角形
如图 ,在Rt△ABC中,∠C=90°,∠A=50。,AB=3.
求∠B和a,b(边长精确到0.1).
参考数据:sin 50。≈0.766,cos 50。≈0.643, tan50。≈1.192
课堂总结
已知斜边c和一锐角∠A,解直角三角形的一般步骤是:
(1)根据∠A+∠B=90°求出∠B;
(2)根据sin A= ,求出a;
(3)根据cos A= ,求出b或根据勾股定理求出b.
课堂练习
在Rt△ABC中,∠C=90°.
(1)若∠B=60°, BC= 则∠A=_______,
AC=________, AB=________;
(2)若∠A=45°,AB=2,则∠B=________,
AC= ________,BC=________.
在Rt△ABC中,∠C=90°,∠B=37°, BC=32,则AC=_.
(参考数据: sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
作业布置
1.教材P9 作业题1,3
2.作业本1.3解直角三角形(1)
的边角关系
直角三角形
解直角三角形
解直角三角形
实际应用
知一边一锐角
解直角三角形
知两边解直角三角形
添设辅助线解直角三角形
知斜边一锐角解直角三角形
知一直角边一锐角解直角三角形
知两直角边解直角三角形
知一斜边一直角解直角三角形
直接抽象出直角三角形
抽象出图形,再添设辅助线求解
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
