1.3解直角三角形第二课时 课件(共17张PPT)
文档属性
| 名称 | 1.3解直角三角形第二课时 课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-13 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
1.3解直角三角形
第一课时
浙教版九年级下册
。
课前复习
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
∠A+∠B=900
a2+b2=c2
C
A
B
斜边
的对边
正弦函数:
A
A
∠
=
sin
的邻边
的对边
正切函数:
A
A
A
∠
∠
=
tan
斜边
的邻边
余弦函数:
A
A
∠
=
cos
。
探 究
如图,在Rt△ABC中,∠C=Rt∠
(1)已知∠A和c,则a= ,b= .
(2)已知∠A和a,则c= ,b= .
(3)已知∠A和b,则c= ,a= .
有斜(斜边)用弦(正弦、余弦) 选乘法
无斜(斜边)有对(对边)
用切(正切) 选除求邻边
用弦(正弦) 选除求斜边
无斜(斜边)有邻(邻边)
用切(正切) 选乘求对边
用弦(余弦) 选除求斜边
C
A
B
b
a
c
课堂练习
在Rt△ABC中,∠C=90°.
(1)若∠B=60°, BC= 则∠A=_______,
AC=________,AB=________;
(2)若∠A=45°,AB=2,则∠B=________,
AC=________,BC=________.
C
A
B
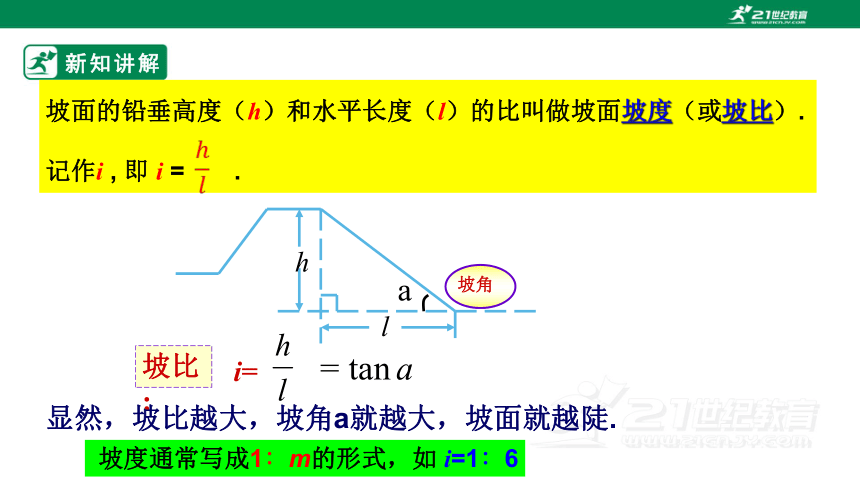
新知讲解
h
l
坡比:
坡角
显然,坡比越大,坡角a就越大,坡面就越陡.
坡面的铅垂高度(h)和水平长度(l)的比叫做坡面坡度(或坡比).
记作i , 即 i = .
i=
坡度通常写成1∶m的形式,如 i=1∶6
课堂练习
1.如图
(1)若h=2cm,l=5cm, 则i= ;
(2)若i=1:1.5,h=2m,则l= ;
2、水库的横断面是梯形ABCD,迎水坡AB的坡度
i=1:2,坝高h=20m,迎水坡的水平宽度= ,
tana= ;
3m
40m
α
A
B
h
C
0.5
例 题
水库堤坝的横断面是梯形.测得BC长为6m,CD长为60m,斜坡的坡比为1:2.5 ,斜坡AB的坡比为1:3,求:
(1)斜坡CD的坡角∠D和坝底的宽(角度精确到0.1。,宽度精确到0.1m);
A
B
D
C
F
E
1:2.5
1:3
(2)若堤坝长150m,问建造这个堤坝需用多少土石方 (精确到1m3)
参考数据:tan 21.8°≈0.40,sin 21.8°≈0.37, cos 21.8°≈0.93
思考:根据坡比的定义你会如何构造图形?出于什么理由?
课堂练习
课本第22页课内练习第1题
参考数据:tan5.2 °≈0.091,sin 5.2°≈0.095, cos 5.2°≈0.995
课堂练习
课本第23页第3题
某村计划挖一个引水渠,渠道的横断面ABCD是一个梯形(如图).已知渠底宽BC为0.8m,渠道深为1.2m,两渠壁AB=CD,坡比均为1:0.5.那么渠口宽AD为多少m
A
B
C
D
课堂练习
1.如图△ABC中,∠A=45°,AB=6cm,AC=8cm.
(1)求△ABC的面积;
(2)若AB=c,AC=b,AB与AC的夹角为α,你能否用含c,b, α的式子表示S△ABC?
A
B
C
6
8
45°
D
(3)在(2)的条件下,当α为多少时,S△ABC有最大值?是多少?
变式1
已知在△ABC中,AB=5cm,AC=4cm,AB和AC的夹角为a,
设△ABC的面积为S(cm2)
(1)若a为锐角,求S关于a的函数解析式;
(2)问何时△ABC的面积最大?最大面积为多少?
课本第23页作业题第6题
变式2
已知在△ABC中,AB+AC=9cm,AB和AC的夹角为300,设当AB为 x(cm)时,△ABC的面积为 S(cm2)
(1)求S关于x的函数解析式;
(2)问何时△ABC的面积最大?最大面积为多少?
课堂总结
图形计算 化归为 解直角三角形
作业布置
1.复习边和角的关系确定
2.作业本:1~5题必做
第6题(A层学生完成)
3.预习:第3课时
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.3解直角三角形
第一课时
浙教版九年级下册
。
课前复习
解直角三角形
1.两锐角之间的关系:
2.三边之间的关系:
3.边角之间的关系
∠A+∠B=900
a2+b2=c2
C
A
B
斜边
的对边
正弦函数:
A
A
∠
=
sin
的邻边
的对边
正切函数:
A
A
A
∠
∠
=
tan
斜边
的邻边
余弦函数:
A
A
∠
=
cos
。
探 究
如图,在Rt△ABC中,∠C=Rt∠
(1)已知∠A和c,则a= ,b= .
(2)已知∠A和a,则c= ,b= .
(3)已知∠A和b,则c= ,a= .
有斜(斜边)用弦(正弦、余弦) 选乘法
无斜(斜边)有对(对边)
用切(正切) 选除求邻边
用弦(正弦) 选除求斜边
无斜(斜边)有邻(邻边)
用切(正切) 选乘求对边
用弦(余弦) 选除求斜边
C
A
B
b
a
c
课堂练习
在Rt△ABC中,∠C=90°.
(1)若∠B=60°, BC= 则∠A=_______,
AC=________,AB=________;
(2)若∠A=45°,AB=2,则∠B=________,
AC=________,BC=________.
C
A
B
新知讲解
h
l
坡比:
坡角
显然,坡比越大,坡角a就越大,坡面就越陡.
坡面的铅垂高度(h)和水平长度(l)的比叫做坡面坡度(或坡比).
记作i , 即 i = .
i=
坡度通常写成1∶m的形式,如 i=1∶6
课堂练习
1.如图
(1)若h=2cm,l=5cm, 则i= ;
(2)若i=1:1.5,h=2m,则l= ;
2、水库的横断面是梯形ABCD,迎水坡AB的坡度
i=1:2,坝高h=20m,迎水坡的水平宽度= ,
tana= ;
3m
40m
α
A
B
h
C
0.5
例 题
水库堤坝的横断面是梯形.测得BC长为6m,CD长为60m,斜坡的坡比为1:2.5 ,斜坡AB的坡比为1:3,求:
(1)斜坡CD的坡角∠D和坝底的宽(角度精确到0.1。,宽度精确到0.1m);
A
B
D
C
F
E
1:2.5
1:3
(2)若堤坝长150m,问建造这个堤坝需用多少土石方 (精确到1m3)
参考数据:tan 21.8°≈0.40,sin 21.8°≈0.37, cos 21.8°≈0.93
思考:根据坡比的定义你会如何构造图形?出于什么理由?
课堂练习
课本第22页课内练习第1题
参考数据:tan5.2 °≈0.091,sin 5.2°≈0.095, cos 5.2°≈0.995
课堂练习
课本第23页第3题
某村计划挖一个引水渠,渠道的横断面ABCD是一个梯形(如图).已知渠底宽BC为0.8m,渠道深为1.2m,两渠壁AB=CD,坡比均为1:0.5.那么渠口宽AD为多少m
A
B
C
D
课堂练习
1.如图△ABC中,∠A=45°,AB=6cm,AC=8cm.
(1)求△ABC的面积;
(2)若AB=c,AC=b,AB与AC的夹角为α,你能否用含c,b, α的式子表示S△ABC?
A
B
C
6
8
45°
D
(3)在(2)的条件下,当α为多少时,S△ABC有最大值?是多少?
变式1
已知在△ABC中,AB=5cm,AC=4cm,AB和AC的夹角为a,
设△ABC的面积为S(cm2)
(1)若a为锐角,求S关于a的函数解析式;
(2)问何时△ABC的面积最大?最大面积为多少?
课本第23页作业题第6题
变式2
已知在△ABC中,AB+AC=9cm,AB和AC的夹角为300,设当AB为 x(cm)时,△ABC的面积为 S(cm2)
(1)求S关于x的函数解析式;
(2)问何时△ABC的面积最大?最大面积为多少?
课堂总结
图形计算 化归为 解直角三角形
作业布置
1.复习边和角的关系确定
2.作业本:1~5题必做
第6题(A层学生完成)
3.预习:第3课时
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
