第四章平行四边形›导学案

八年级数学第四章导学案及答案：
4.1 多边形（1）
【课前预习导学】
由不在同一条直线上的三条线段____________________形成的图形叫做三角形.
三角形的内角和等于_________，三角形的外角和等于__________.
证明几何命题的一般步骤是什么？
4．从四边形的一个顶点出发引一条对角线，可将四边形分成两个三角形，这样四边形的四个内角和就转化为两个三角形的内角和，这样，你知道四边形的内角和等于多少度吗？
5．四边形ABCD中，，则等于（ ）
A． 40° B. 60° C．100° D. 120°
【课外资料导学】 数学思想方法—转化思想
转化思想是指在研究和解决数学学问题时由一种教学对象转化为另一种数学对象时所采用的数学方法的指导思想.运用转化思想可以把生疏的新的问题转化成熟悉的旧的问题，把复杂的问题转化成简单的问题，把一般问题转化成特殊的问题，从而完成数与数的转化，形与形的转化，数与形的转化.如本节课中，将四边形问题转化成三角形问题，从而使问题得到解决.
【课中生成导学】
1.已知四边形各角度数之比时，通常可用比值列式直接计算方法以及应用辅导未知数的代数方法，求出四边形四个内角的度数.通过设辅导未知数并列出方程或方程组，使有关的几何量之间的关系显现出来，从而使所研究的问题比较简捷地加以解决的数学思想方法叫___________.
2.本节课中还用到了其它的数学思想方法，如在学习四边形的有关概念时用到了___________数学思想方法，根据三角形的定义得出四边形的定义.在学习四边形内角和与外角和时又用到了___________数学思想方法，将四边形的有关问题转化成三角形的有关问题.
3. (1)四边形的四个内角可以都是锐角吗？可以都是钝角吗？可以都是直角吗？为什么？
(2)一个四边形中，最多可以有几个锐角？最多有几个钝角？
【课堂测评导学】(共10分)
1．在四边形ABCD中， 160°，比大60°，则为（ ）
A．70° B．80° C． 120° D．130°
2.在四边形ABCD中，，则的度数分别为______________________.
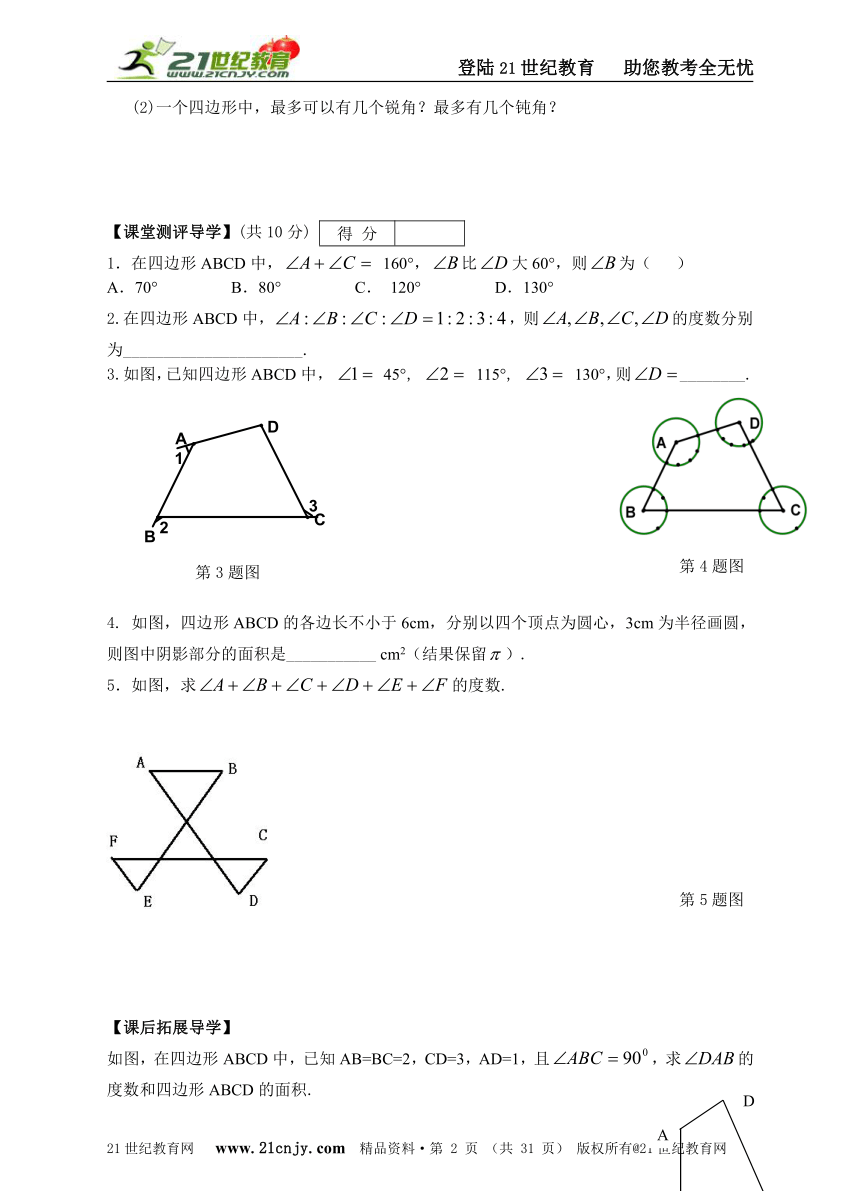
3.如图，已知四边形ABCD中， 45°, 115°, 130°，则________.
4. 如图，四边形ABCD的各边长不小于6cm，分别以四个顶点为圆心，3cm为半径画圆，则图中阴影部分的面积是___________ cm2（结果保留）.
5．如图，求的度数.

【课后拓展导学】
如图，在四边形ABCD中，已知AB=BC=2，CD=3，AD=1，且，求的度数和四边形ABCD的面积.
4.1 多边形（2）
【课前预习导学】
1．在同一平面内，由不在同一条直线上的若干条线段（线段的条数不小于3）首尾顺次相接所组成的图形叫做 .
2. 从五边形的一个顶点出发的对角线有 条，它把五边形分成 个三角形，所以五边形的内角和等于 .
3. 一个多边形的内角和是720°，这个多边形的边数是（　　）
A．4 B．5 C．6 D．7
4．边形的内角和为，则= .
5. 一个多边形的每一个外角都等于18°，它是___________边形.
【课外资料导学】 数学思想方法—从特殊到一般
从特殊到一般的数学思想方法，即先观察一些特殊的事例，然后分析它们共同具有的特征，作出一般的结论.新《数学课程标准》指出要发展学生的符号感，其中符号感的一个主要表现是要求学生能从具体情境中抽象出数量关系和变化规律，并用符号来表示，而列代数式是实现这一目标的具体途径.如本节课在探索多边形的内角和时，先从边数为3、4、5、6这一类特殊的多边形内角和的研究从而得出边数为的多边形的内角和.
【课中生成导学】
1. n边形的内角和为 ，n边形的外角和为 .
2. n边形从一个顶点出发的对角线有_____________条 (n≥3),n边形共有对角线 _____________条(n≥3) .
3.过n边形一个顶点的所有对角线将这个多边形分成____________个三角形.
4.对角线是解决多边形问题的常用辅导线.
5.四边形是多边形中唯一一个内角和与外角和相等的多边形.
【课堂测评导学】(共10分)
1．一个多边形的内角和与外角和相等，则这个多边形是（ ）
A．四边形 B．五边形 C．六边形 D．八边形
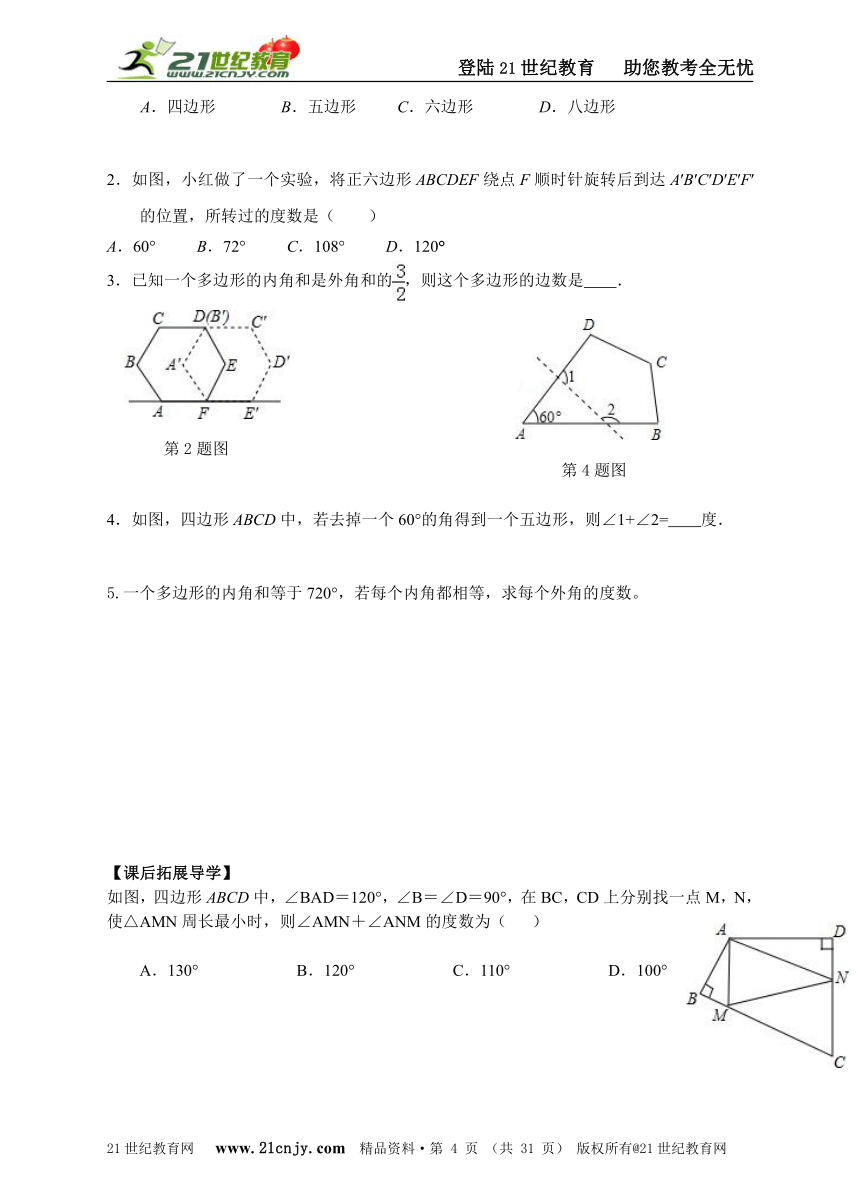
2．如图，小红做了一个实验，将正六边形ABCDEF绕点F顺时针旋转后到达A′B′C′D′E′F′的位置，所转过的度数是（　　）
A．60° 　　B．72°　　 C．108°　　 D．120°
3．已知一个多边形的内角和是外角和的，则这个多边形的边数是　　．
4．如图，四边形ABCD中，若去掉一个60°的角得到一个五边形，则∠1+∠2=　　度．
5.一个多边形的内角和等于720°，若每个内角都相等，求每个外角的度数。
【课后拓展导学】
如图，四边形ABCD中，∠BAD＝120°，∠B＝∠D＝90°，在BC，CD上分别找一点M，N，使△AMN周长最小时，则∠AMN＋∠ANM的度数为（ ）
A．130° B．120° C．110° D．100°
4.2 平行四边形及其性质（1）
【课前预习导学】
1．如图，任意剪两个全等的锐角三角形，然后用这两个全等锐角三角形拼四边形.你能拼出几种不同形状的四边形？
2．两组对边分别 的四边形叫做平行四边形，平行四边形用符号“ ”表示．
3．已知平行四边形ABCD中，∠A=60°，则∠B= ，∠C= ，∠D= ．
4．已知平行四边形ABCD中，∠B=4∠A，则∠C为（　　）
　　A．18°　　B．36°　　C．72°　　D．144°
5. 在平行四边形ABCD中，若AB=3cm，AD=4cm，则它的周长为　 　cm．
【课外资料导学】
我们周围的世界充满着大自然的杰作和人类的创造物，各式各样的物体，无不包含了许多的几何形体．人们从日常的生产、生活中的物体抽象出几何图形，并提炼出它们的性质及识别的方法，然后又利用它们为生产、生活服务．如图，有一种衣架，是用同样长的木条构成的几个相连的菱形，顶点处都有挂钩，不仅美观，而且实用，这种衣帽架是根据平行四边形的不稳定性设计的，它的好处是：(1)利用不稳定性，可以根据需要改变挂钩间的距离；(2)利用平行四边形对边平行且相等的原理，最后可以使平行木条完全靠拢，收起来不占地方．
【课中生成导学】
【课堂测评导学】(共10分)
1．如图，将平行四边形ABCD的一边BC延长至E，若∠A=110°，则∠1=________．
2．平行四边形ABCD中，已知点A（﹣1，0），B（2，0），D（0，1），则点C的坐标为　 　．
3. 平行四边形ABCD中，∠A：∠B=13：5，则∠A和∠B的度数分别为（ ）
A．80°，100° B．130°，50°
C．160°，20°　　D．60°，120°
4．如图，平行四边形ABCD的周长为30cm，△ABC的周长为25cm，则对角线AC的长为（ ）
　A．10cm　　B．15cm　　C．5cm　　D．无法计算


5．．如图，在平行四边形ABCD中，∠ABC=3∠A，点E在CD上，CE=1，EF⊥CD于点E，BC=1，求BF的长．
【课后拓展导学】
如图，是用一平行四边形纸条沿对边AB，CD的中点E，F所在直线折成的V形图案，已知图中∠1=60°，求∠2的度数．
4.2平行四边形的性质（2）
【课前预习导学】
1．　 　　 　　 　　 叫做两条平行线之间的距离，所图所示，线段　 　　　　的长就是平行线与之间的距离．
2．请量一量你的数学课本宽，在测量数学课本宽时，你量的位置与其它同学相同吗？测量结果呢？如果所得的结果相同，为什么在不同的位置测量，却得到相同的结果？
3．如图，已知平行四边形ABCD中，AB=4，BC=6，BC边上的高AE=2，则DC边上的高AF的长是
?　 　．
4． 如图，直线∥,△ABC与△DBC的面积相等吗？你还能再画出一些与△ABC面积相等的三角形吗？
【课外资料导学】 利用平行四边形的性质 巧解生活难题（一）
平行四边形是特殊的四边形，在实际生活中着广泛的应用，对于生活中的一些实际问题，同学们可以巧借平行四边形的相关性质加以解决．
一、比较线路长短
图1是某区部分街道示意图，其中CE垂直平分AF，BC=DA，BC∥DF，FD//BC．从B站乘车到E站只有两条路线有直接到达的公交车，路线1是B－D－A－E，路线2是B－C－F－E，请比较两条路线路程的长短，并说明理由．.
【分析】本题是一道设计比较新颖的实际问题,要比较两条线段的长短,首先要从实际问题构建数学模型。实际上线路1,可用线段BD、DA、AE的和来表示；线路2可用线段BC、CF、FE的和来表示，本题就可以通过比较BD+DA+AE和BC+CF+FE的大小即可．
【课中生成导学】
1.在两条平行线之间的距离概念中，特别要注意的是其中的线段的长度是指垂线段的长度，而并非任一条线段的长度都是距离。
2.夹在两条平行线间的平行线段相等，夹在两条平行线间的垂线段相等．
【课堂测评导学】(共10分)
1. 已知平行四边形ABCD中，AB=20厘米，AD=16厘米，AB与CD之间的距离为8厘米，求AD与BC之间的距离为　 　　 ．
2．如图，平行四边形ABCD中，∠A=60°，AD=6cm，则线段AB，CD之间的距离为 　　 ．
3．M是平行四边形ABCD边AD上任意一点，三角形CBM的面积为S，三角形ABM的面积为S1，三角形CDM的面积为S2，则S与S1+ S2的大小关系是　 　　 　．
4．如图， ∥，AD∥BC，CD：CF=2:1，若△CEF的面积为10，则四边形ABCD的面积为　 　．
5．已知：如图，平行四边形ABCD中，AE⊥BC于点E，CF⊥AD于点F.
求证：△ABE≌△CDF.
【课后拓展导学】
如图，在平行四边形ABCD中，AE⊥BC于E，AF⊥CD于F，，EC=2cm，CF=1cm，求平行四边形ABCD的周长.
4.2 平行四边形的性质（3）
【课前预习导学】
1.任意画一个平行四边形ABCD，连接对角线AC，BD，相交于点O，找一找图中有几对全等三角形？
2.由（1）全等三角形可得，平行四边形的对角线 .
3.平行四边形不一定具有的性质是（ ）
A．对角线互相平分　　 B．对边平行　　 C．对角线互相垂直　　 D．对边相等
4. 若平行四边形ABCD的两条对角线AC，BD交于O点，且AC=20，BD=14，则AO= ， BO= .
5.在平行四边形ABCD中，对角线AC，BD交于O点，若△AOB的面积为3，则平行四边形ABCD的面积为 .

【课外资料导学】 利用平行四边形的性质 巧解生活难题（二）
二、扩大池塘的面积
如图2，一口呈四边形的池塘，在它的四周A，B，C，D处各有一棵桃树，如果想把池塘扩大一倍，而保住四棵桃数不动，并要求扩建的池塘为平行四边形的形状，请你判断这一想法能否实现？
【分析】由于四棵桃树分别在四边形的顶点，所以要想把池塘改成平行四边形，切面积扩大一倍，则四棵桃树应在平行四边形的边上，且每条边上都有一棵桃树.为此只要过四边形的顶点A、C两点作对角线BD的平行线，过顶点B，D作对角线AC的平行线即可．
解：如图1，分别过点A、C作BD的平行线，过点B、D作AC的平行线，四条线分别相交于点E，F，G，H．由作图可知四边形AEBO，BFCO，CGDO，DHAO均为平行四边形，且△ABO，△BOC，△COD，△DOA的面积分别为平行四边形AEBO，BFCO，CGDO，DHAO面积的一半，所以平行四边形EFGH为四边形ABCD面积的一半．
【课中生成导学】
1.
2.过对角线交点的任一条直线都将平行四边形分成面积与周长相等的两部分
【课堂测评导学】(共10分)
1．平行四边形的一条边长为7，则它的两条对角线长可以是（ ）
A．6和3　　 B．5和8　　 C．20和5　　 D．10和12
2.如图，在四边形ABCD中，AB∥CD，AD∥BC，AC，BD相交于点0，若AC=6，则线段AO的长度等于　 .
3.平行四边形ABCD的对角线AC、BD交于O点，AB=5cm，△AOB的周长比△BOC的周长短3cm，则AD的长
为 cm.
4．如图，在平行四边形ABCD中，（AB≠BC），直线EF
经过其对角线的交点O，且分布交AD，BC于点M，N，交BA，DC的
延长线于点E，F，下列结论：? ①AO=BO；②OE=OF；③△EAM≌△CNF，
其中正确的是 .?（填序号）
5．如图，四边形ABCD和四边形BEDF都是平行四边形，求证：AE=CF.
【课后拓展导学】
如图，平行四边形ABCD中，AC⊥AB,AC与BD相交于点O，OC=1，CD=.
求BD的长；
求平行四边形ABCD的周长；
求平行四边形ABCD的面积.
4.3 中心对称
【课前预习导学】
1．如果一个图形沿着一条直线折叠，直线两旁的部分能够相互重合，那么这个图形叫做 ，这条直线叫做 ．
2．轴对称图形的性质：对称轴 连结两个对称点之间的线段．
3．下列图形中，不是轴对称图形的是（ ）
A．线段 B．等腰三角形 C．圆 D．平行四边形
4．如图，是由大小一样的小正方形组成的网格，的三个顶点均落在小正方形的顶点上．在网格上能画出的三个顶点都落在小正方形的顶点上，且与成轴对称的三角形共有（　　）
Ａ．个 Ｂ．个 Ｃ．个 Ｄ．个
5．平面直角坐标系中，与点（2，－3）关于原点中心对称的点是（ ）
A． （－3，2） B． （3，－2） C． （－2，3） D． （2，3）
【课外资料导学】 生活中的中心对称
中心对称应用于广告商标的设计制作，往往能以简单的色彩、线条，勾画出生动、富于创意和内涵的作品．因而只要你细心观察，就不难发现，原来中心对称就在我们身边！
旋转的物体必须具有稳定性，而中心对称的设计恰恰满足了旋转物体的这一需求．因而在工农业生产制作转动工具时，都不可避免地考虑应用中心对称的设计，小的如日常生活中单车、闹钟内的齿轮，电风扇的扇叶；大的如推动飞机、轮船的轮桨，风力发电用的风车等等另外，在日常使用的一些生活工艺品（如：地毯、挂毯），也不难发现中心对称的影子！
【课中生成导学】
1.轴对称与中心对称的比较
轴对称
中心对称
定义三要点
1．有一条对称轴——直线
1．有一个对称中心——点
2．图形绕对称轴翻转180度
2．图形绕中心旋转180度
3．翻转后与另一个图形重合
3．旋转后与另一个图形重合
性质
1．两个图形是全等形
1．两个图形是全等形
2．对称轴是对应点连线的垂直平分线
2．对称中心是对应点连线的中点
3．对应线段或延长线相交，交点在对称轴上
3．对应点连线都经过对称中心
2. 在直角坐标系中，点（，）关于原点对称的点的坐标是（-，-），关于轴对称的点的坐标是（，-），关于轴对称的点的坐标是（-，）.
【课堂测评导学】(共10分)
1．下列汽车标志中，可以看作是中心对称图形的是
2．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
3．若点（m-1，3）与点（2，n+3）关于原点对称，则m= ， n= .
4．如图，△AOB中，顶点A，B，O均在格点上，画出△AOB绕点O旋转180°后的三角形．（不要求写作法，证明，但要注明结果）
5．图①，图②均为7×6的正方形网格，点A，B，C在格点上．（1）在图①中确定格点D，并画出以A，B，C，D为顶点的四边形，使其为轴对称图形．（画一个即可）（2）在图②中确定格点E，并画出以A，B，C，E为顶点的四边形，使其为中心对称图形．（画一个即可）
【课后拓展导学】
在平面直角坐标系中，正方形ABCD的顶点坐标分别为A(1,1),B(1,-1),C(-1,-1),D(-1,1),y轴上有一点P(0,2).作点P关于点A的对称点,作点关于点B的对称点,作点关于点C的对称点,作点关于点D的对称点,作点关于点A的对称点,作点关于点B的对称点…,按此操作下去,则点的坐标为( )
A.(0,2) B. (2,0) C. (0,-2) D.(-2,0)
4.4 平行四边形的判定定理（1）
【课前预习导学】
1．根据平行四边形的定义，可得平行四边形的第一种判定方法： ．
2．平行四边形的边、角分别有哪些性质？
3．逆向思维：将上题中的条件与结论交换位置，写出新的结论．并猜想这些结论的真假．
4．已知四边形的边长依次为下列各数，则可以判断是平行四边形的是（ ）
A．2 ，3 ，4 ，5 B．2 ，3 ，2 ，3 C．2 ，3 ，3 ，2 D．2 ，3 ，2 ，4
5．下面给出了四边形ABCD中∠A，∠B,∠C，∠D的度数之比，其中能判断是平行四边形的是（ ）
A．1：2 ：3 ：4 B．2：2：4 ：4 C．2：3：2：3 D．2：3 ：3 ：2
【课外资料导学】 利用平行四边形的性质 巧解生活难题（三）
三、计算影子的面积
如图3，阳光透过长方形玻璃投射到地面上，地面上出现了一个明亮的四边形，小刚用量角器量出了一条对角线与一边垂直，用直尺量出了四边形的四条边分别是30cm，50cm，30cm，50cm，小刚说用这些数据就能计算出四边形的面积，你知道小刚是如何计算的吗？这样计算的根据是什么？
【分析】根据小明测量的数据可知这个四边形的对边相等，由此可确定该四边形为平行四边形，可画出如图所示的图形，根据已知可得AB⊥AC，AB=30cm，BC=50cm，根据勾股定理可以计算出△ABC的面积和△ACD的面积，所以计算四边形ABCD的面积．
解：如图4，根据已知条件可四边形ABCD是平行四边形，所以AB//CD，因为AB⊥AC，所以CD⊥AC，所以△ACD为直角三角形.
在Rt△ABC中，因为AB2+AC2=BC2，所以AC2=502-302=402，所以AC=40，所以△ABC的面积为×40×30=600（cm2）.同样△ACD的面积为600cm2，所以四边形ABCD的面积为1200cm2．
【课中生成导学】
【课堂测评导学】(共10分)
1.不能判定一个四边形是平行四边形的条件是（ ）
A.两组对边分别平行 B.一组对边平行另一组对边相等
C.一组对边平行且相等 D.两组对边分别相等
2．下列条件中，能判定四边形ABCD是平行四边形的是（ ）
A．AB∥CD,AD=BC B．∠A=∠B,∠C=∠D C．AB=AD,CB=CD D．AB=CD,AD=BC
3.已知四边形ABCD中，AB=CD，要使四边形ABCD为平行四边形，需添加一个条件是 ．（只需填一个你认为正确的条件）
4．若A，B，C，D在同一平面，从①AB∥CD；②AB=CD；③BC∥AD；④BC=AD．这四个条件中任意选两个，能使四边形ABCD为平行四边形的选法有 ．（只填序号）
5．如图，在平行四边形ABCD中，E、F分别在边AD，BC上，且AE＝CF．
证明：(1)△ABE≌△CDF；
(2)四边形BFDE是平行四边形．
【课后拓展导学】
如图，点D是△ABC的边AB的延长线上一点，点F是边BC上的一个动点（不与点B重合）．以BD，BF为邻边作平行四边形BDEF，又APBE（点P，E在直线AB的同侧），如果BD=AB，那么△PBC的面积与△ABC面积之比为（　　）
A． B． C． D．
4.4 平行四边形的判定定理（2）
【课前预习导学】
1． 上节课我们学了平行四边形的哪些判定方法？
2．平行四边形的对角线有什么性质？
3．逆向思维：将上题中的条件与结论交换位置，写出新的结论．并猜想这个结论的真假．
4．下面几组条件中，能判定一个四边形是平行四边形的条件是（ ）
A.一组对边相等 B.两条对角线互相平分
C.一组对边平行 D. 两条对角线互相垂直
5． 四边形ABCD的对角线AC，BD交于点O，下列条件不能判定四边形ABCD是平行四边形的是（　　）
A．AD∥BC且AD=BC B．OA=OC，OB=OD
C．AB=DC，AD=BC D．AD∥BC，AB=DC
【课外资料导学】利用平行四边形的性质 巧解生活难题（四）
四、等分地块的面积
如图5，ABCD是老王家的一块平行四边形田地，P为水井，现要把这块田平均分给两个儿子,为了方便用水，要求两个儿子分到的地都与水井相邻，请你来设计一下，并说明你的理由.
【分析】 我们说只要满足所分的两块地面积相等，且都与水井相邻就可以。那么可以考虑利用平行四边形的性质（平行四边形的对角线互相平分）来解题。找到两条对角线的交点，则交点和水井所在的直线将田地分成面积相等的两块.
　 解：设对角线AC，BD交于O，如图6，过O、P作直线交BC，AD于E、F，则线段EF分割的这两块田地符合要求.理由如下：易证OE=OF，BE=ＤF，AF=CE（把证线段相等转化为证三角形全等），四边形ABEF绕点O旋转180°，就与四边形CDFE重合，这两部分面积相等,又点P（井）在EF上，符合水井和两块地相邻的要求，故此种分法符合要求.
实际生活中有很多需要直接或间接用平行四边形的性质来解决的问题，只要我们牢牢把握住平行四边形的性质并加以灵活地运用，就可以巧妙地解决生活中的数学难题.
【课中生成导学】
【课堂测评导学】(共10分)
1．如图，在四边形ABCD中，AB∥CD，AD∥BC，AC、BD相交于点0．若AC=6，则线段AO的长度等于____________．
2．四边形ABCD中，对角线AC、BD相交于点O，给出下列四组条件：①AB∥CD，AD∥BC；②AB=CD，AD=BC；③AO=CO，BO=DO；④AB∥CD，AD=BC．其中一定能判断这个四边形是平行四边形的条件共有（　　）
A．1组 B．2组 C．3组 D．4组
3.延长△ABC的中线AD到E，使DE=AD，则四边形ABEC为______________形．
4.如图，在△ABC中，点D，E分别是AB，AC的中点，延长DE到点F，使EF=DE，
连接AF,CF，若AB=10，BC=8，则四边形BCFD的周长是___________．
5.如图，在平行四边形ABCD中，E,F是直线BD上的两点，且DE=BF，你认为AE=CF吗？试说明理由.
【课后拓展导学】
如图，△ABC为等边三角形，D、F分别为CB、BA上的点，且CD=BF以AD为一边作等边三角形ADE．四边形CDEF是平行四边行吗？说说你的理由．
4.5 三角形的中位线
【课前预习导学】
1．三角形中，连接______________________的线段叫做三角形的中线，三条中线交于三角形内一点．
2．如图，直角三角形ABC中，∠ACB=90°，D是AB边上的中点，CD=3，则AB=___________．
3．如图，△ABC中， AD是BC边上的中线，△ABD的面积为12cm2，则△ABC的面积为___________ cm2．
4.连接三角形两边中点的线段叫做___________．
5．如图，在△ABC中，D，E分别是边AB，AC的中点，BC=8，则DE=___________．
【课外资料导学】 一题多解
一题多解是开发智力、培养能力的一种行之有效的方法,它对沟通不同知识间的联系,开拓思路,培养发散思维能力,激发学生的学习兴趣都十分有益.在学习过程中应注重一题多解，一题多解以其思维的发散性,探求问题的多方向性、多层次性、多侧面性,解法转化的灵活性,使数学解题的方法五彩缤纷,各具特色.在教学及学习中运用一题多解,是学好数学的一种良好方法.运用一题多解,总结各种解法,有利于学生的知识系统化、深刻化;运用一题多解,有利于培养良好的数学思维品质;运用一题多解,有利于学生寻求规律,更好地学会求解数学问题;运用一题多解,有利于开发学生的智力及培养思考问题的能力.本节课三角形中位线定理的证明就是一道典型的一题多解的好题.
【课中生成导学】
1.三角形的中位线定理：
三角形的中位线平行于第三边，并且等于第三边的一半.
几何语言：
∵DE是△ABC的中位线（或AD=BD,AE=CE)
∴DE∥BC,且DE=1/2BC
2.中点四边形
顺次连接四边形各边中点的线段组成一个平行四边形.
3.方法点拨：
在处理问题时,要求同时出现三角形及中位线
①有中点连线而无三角形,要作辅导线产生三角形
②有三角形而无中位线,要连结两边中点得中位线
4．注意三角形中线与三角形中位线的区别与联系
【课堂测评导学】(共10分)
1．如图，在△ABC中，AB=AC，AD⊥BC，垂足为D，E是AC的中点．若DE=5，
则AB的长为 ．
2．已知△ABC的周长等于16，D，E分别是AB，AC的中点，那么△ADE的周长等于（ ）；
A. 4 B. 6 C. 8 D. 10
3．（2011天津）如图，点D，E，F分别是△ABC的边AB，BC，CA的中点，连接DE，EF，FD，则图中平行四边形的个数为　 　．
4．如图，已知△ABC的周长为1，连结△ABC三边的中点构成第二个三角形，再连结第二个三角形三边的中点构成第三个三角形，依此类推，第2013个三角形的周长为（ ）
A． B． C． D．

5．如图，已知E为平行四边形ABCD中DC边的延长线上的一点，且CE=DC，连结AE，分别交BC，BD于点F，G，连结AC交BD于O，连结OF.
求证：AB=2OF.
【课后拓展导学】
如图，△ABC的三边长分别为AB＝14，BC＝16，AC＝26，P为∠A的平分线AD上一点，且BP⊥AD，M为BC的中点，求PM的长.
4.6反证法
【课前预习导学】
1．“a A．a≠b B．a>b C．a=b D．a=b或a>b
2．用反证法证明“同一平面内，若a⊥c，b⊥c，则a∥b”时，应假设（ ）
A．a不垂直于c B．a，b都不垂直于c
C．a⊥b D．a与b相交
3．完成下列证明过程
已知：∠A，∠B，∠C是△ABC的三个内角，求证：∠A，∠B，∠C三个角中不可能有两个直角．
证明：假设　　　　　　　　　　　　　　　　　　，
则有 ，
这与“　　　　　　　　　　　　　　　　　”相矛盾，
∴ 假设不成立，即求证的命题成立，
∴ ∠A，∠B，∠C三个角中不可能有两个直角．
【课外资料导学】
数学思想方法中的逻辑型思想方法是“作为一般科学方法论的逻辑所包含的思想，是指“根据事实材料，遵循逻辑规律、规则，形成概念、作出判断和进行推理的方法”．逻辑型思想方法包括完全归纳法、反证法、演绎法、特殊化方法等，这类方法都具有确定的逻辑结构．数学是现实世界的抽象反映和人类经验的总结，都经历着由特殊到一般的归纳过程．
【课中生成导学】
1．反证法的一般证明步骤：
一反设：假设待证命题不成立，或命题的反面成立；
二归缪：以假设为条件，结合已知条件，学过的公理、定理、定义、法则进行推理推理，得出与已知条件或正确命题相矛盾的结论；
三写出结论：肯定原命题成立；
2．用反证法证题时，首先要正确分清命题的题设和结论，正确全面地否定结论．如果结论的反面不止一种情形，那么必须把各种可能性都列出来，并且逐一加以否定之后，才能肯定原结论正确．
【课堂测评导学】（10分）
1．请说出下列结论的反面:
（1）d是正数
（2）a≤5．
2．用反证法证明“已知a＜|a|，求证：a必为负数”时，应假设 ．
3．用反证法证明命题“在一个三角形中，如果两条边不相等，那么它们所对的角也不相等”时，应假设 ．
4.完成下列证明．
如图，在△ABC中，若∠C是直角，那么∠B一定是锐角．
证明：假设结论不成立，则∠B是______或______．[来源:Zxxk.
当∠B是____时，则_________，这与________矛盾；
当∠B是____时，则_________，这与________矛盾．
综上所述，假设不成立． ∴∠B一定是锐角
5．用反证法证明：连结直线外一点和直线上所有点的线段中，垂线段最短．
【课后拓展导学】
地理老师在黑板上画了一幅世界五大洲的图形，并给每个洲都写上了代号，然后，他请5个同学每人认出2个大洲来，5个同学的回答是：
甲：3号是欧洲，2号是美洲；
乙：4号是亚洲，2号是大洋洲；
丙：1号是亚洲，5号是非洲；
丁：4号码是非洲，3号是大洋洲；
戊：2号码是欧洲，5号是美洲；
地理老师说：“你们每个人都认对了一半”，请问，每个号码各代表什么洲呢？
答案：
4.1多边形（1）
【课前预习导学】
首尾顺次相接
180°；360°
（1）根据题意,画出图形；（2）分清命题的条件和结论，结合图形，在“已知”中写出条件，在“求证”中写出结论；（3）在“证明”中写出推理过程
360°
D
【课中生成导学】
方程思想；
类比；转化
（1）不可以；不可以；可以 （2）最多有3个锐角；最多有3个钝角
【课堂测评导学】
D
36°，72°，108°，144°
110°
9
360°
【课后拓展导学】
∠DAB=135°，四边形ABCD的面积为
4.1 多边形（2）
【课前预习导学】
多边形
2；3；540°
C
14
二十
【课中生成导学】
；360°
；
【课堂测评导学】
A
A
5
240°
60°
【课后拓展导学】
B
4.2 平行四边形 及其性质（1）
【课前预习导学】
1． 如图所示，
2．平行；
3． 120°，60°，120°
4．B
5．14
【课堂测评导学】
70°
B
（3，1）
A
【课后拓展导学】
600
4.2 平行四边形 及其性质（2）
【课前预习导学】
一条直线上的任一点到另一条直线的距离；AB
略
3
相等，图略
【课堂测评导学】
10
S=S1+ S2
40
5．略
【课后拓展导学】
12cm
4.2 平行四边形的性质（2）
【课前预习导学】
△AOB≌△COD, △AOD≌△COB, △ABD≌△CDB, △ADC≌△CBA,
互相平分
C
4．10，7
5. 12
【课堂测评导学】
D
3
8
②③
证明：连接BD交AC于O，∵四边形ABCD和四边形BEDF都是平行四边形，∴AO=CO， EO=FO∴AO-AE=CO-CF．即AE=CF
【课后拓展导学】
（1）BD= （2）周长为 （3）面积为
4.3 中心对称
【课前预习导学】
轴对称图形；对称轴
垂直平分
D
Ｃ
Ｃ
【课堂测评导学】
A
D
m=-1， n=-6
5.略
【课后拓展导学】D
4.4 平行四边形的判定定理（1）
【课前预习导学】
两组对边分别平行的四边形是平行四边形
平行四边形的对边平行且相等；平行四边形的对角相等
对边平行且相等的四边形是平行四边形；对角相等的四边形是平行四边形；真命题
B
C
【课堂测评导学】
B
D
答案不唯一.AB∥CD或 AD=BC或 ∠A+∠D=180°或∠B+∠C=180°等
①③；②④；①②；③④
5．证明：（1）∵四边形ABCD是平行四边形，∴∠A=∠C，AB=CD，
在△ABE和△CDF中，
∵，∴△ABE≌△CDF（SAS）；
（2）∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC，
∵AE=CF，∴AD﹣AE=BC﹣CF，即DE=BF，
∴四边形BFDE是平行四边形．
【课后拓展导学】
D
4.4 平行四边形的判定定理（2）
【课前预习导学】
两组对边分别平行的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对边
分别相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形
平行四边形的对角线互相平分
对角线互相平分的四边形是平行四边形；真命题
B
D
【课堂测评导学】
3
C
平行四边
26
略
【课后拓展导学】
四边形CDEF是平行四边形．
连接BE，∵AB=AC，∠EAD—∠DAB=∠BAC—∠DAB，
∴∠EAB=∠CAD，AE=AD（△ADE是等边三角形），
∴△AEB≌△ADC，
∴∠ABE=∠ACD=60°．CD=EB
∵CD=BF，∴BE=BF，∴△BEF是等边三角形．∴EF=CD．
∵△ADC≌△CBF．∴AD=CF．
∵AD=DE，∴CF=DE．
∴四边形CDEF是平行四边形．
。
4.5 三角形的中位线
【课前预习导学】
一个顶点和它所对边的中点
6
24
三角形的中位线
4
【课堂测评导学】
10
C
3
C
5．证明：∵四边形ABCD是平行四边形，∴AB=CD，OA=OC．
∴∠BAF=∠CEF，∠ABF=∠ECF．
∵CE=DC，
在平行四边形ABCD中，CD=AB，
∴AB=CE．
∴在△ABF和△ECF中，
，∴△ABF≌△ECF，∴BF=CF．
∵OA=OC，∴OF是△ABC的中位线，∴AB=2OF．
【课后拓展导学】
PM＝6
4.6反证法
【课前预习导学】1．D；2．D；3．∠A，∠B，∠C三个角中至少有两个是直角，∠A+∠B+∠C＞180°，三角形的内角和是180°
【课堂测评导学】1．（1）d是非正数（d≤0）；（2）a＞5；2．a为非负数；3．三角形中有两个角相等；4．直角，钝角，直角，∠A+∠B+∠C＞180°，三角形的内角和是180°，钝角，∠A+∠B+∠C＞180°，三角形的内角和是180°5．证明略
【课后拓展导学】1代表亚洲，2代表大洋洲，3代表欧洲，4代表非洲，5代表美洲
【课后练习】
1．C；2．同旁内角不互补，即同旁内角的和不等于180°；3．AB，CD，＞，三角形的一个外角大于任何一个与它不相邻的内角，已知∠1=∠2；4，B；5．∠A不是锐角；6．略；7．略；8，略；9．证明：假设是有理数，则（a，b互质），两边平方得：，所以b是偶数，即是4的倍数，故a也是偶数，这与a，b互质矛盾，故假设不成立，原命题成立．