第五章特殊平行四边形›导学案
文档属性
| 名称 | 第五章特殊平行四边形›导学案 |  | |
| 格式 | zip | ||
| 文件大小 | 256.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-02-27 15:37:51 | ||
图片预览




文档简介
八年级数学导学案及答案:
5.1矩形(1)
【课前预习导学】
矩形具有一般平行四边形都有的性质是:
邻角____________;
对角___________;
对角线________________;
对边_________且_____________.
2.矩形具有而一般平行四边形不具有的特殊性质是:
(1)_____________________________________.
(2)_____________________________________.
3.已知一矩形的周长是24cm,相邻两边之比是1:2,那么这个矩形的面积是 ( )
A.24cm2 B.32cm2 C.48cm2 D.128cm2
4.如图,在矩形ABCD中,,求这个矩形的周长.
【课外资料导学】
黄金矩形
短边与长边之比为黄金比即0.618的矩形,称作黄金比矩形,也称作黄金率矩形.公元前5世纪的古希腊建筑师已经晓得这种协调性的影响.巴特农神殿就是应用黄金矩形的一个早期建筑的例子.那时的古希腊人已经具有黄金均值及如何作它的知识,还知道如何近似于它以及如何用它来构造黄金矩形.除了影响建筑之外,黄金矩形还出现在艺术中.在公元1509年L·帕西欧里的《神奇的比例》一书中,达·芬奇为人体结构中的黄金均值作了图解.黄金均值用在艺术上是以生动的对称技巧为标志.A·丢勒、G·西雷特、P·曼诸利安、达·芬奇、S·达利、G·贝娄等人,都在他们的一些作品中用黄金矩形去创造富有生气的对称.
【课中生成导学】
1. 矩形的定义: .
2. 矩形是一种特殊的平行四边形,它具有平行四边形的性质,如:
(1)两组对边分别 ; (2)对角 、邻角 ; (3)对角线 ,两条对角线把它分成四个面积相等的三角形; (4)是一个 对称图形.
3. 矩形是一个特殊的平行四边形,它除了具有平行四边形所具备的特征外,还具备一般平行四边形所不具备的特征,如: (1)矩形的四个角都是 ; (2)矩形的对角线除了互相平分外,还会 ; (3)矩形的面积等于两邻边的乘积; (4)矩形的两条对角线把矩形分成四个面积相等的 三角形; (5)矩形还是一个 对称图形,并且有 条对称轴.
【课堂测评导学】(10分)
1.下面的图形中,既是轴对称图形,又是中心对称图形的是 ( ) A. 角 B. 任意三角形 C. 矩形 D. 等腰三角形
2.矩形具有而一般平行四边形不具有的性质是 ( ) A. 对角相等 B. 对边相等 C. 对角线相等 D. 对角线互相平分
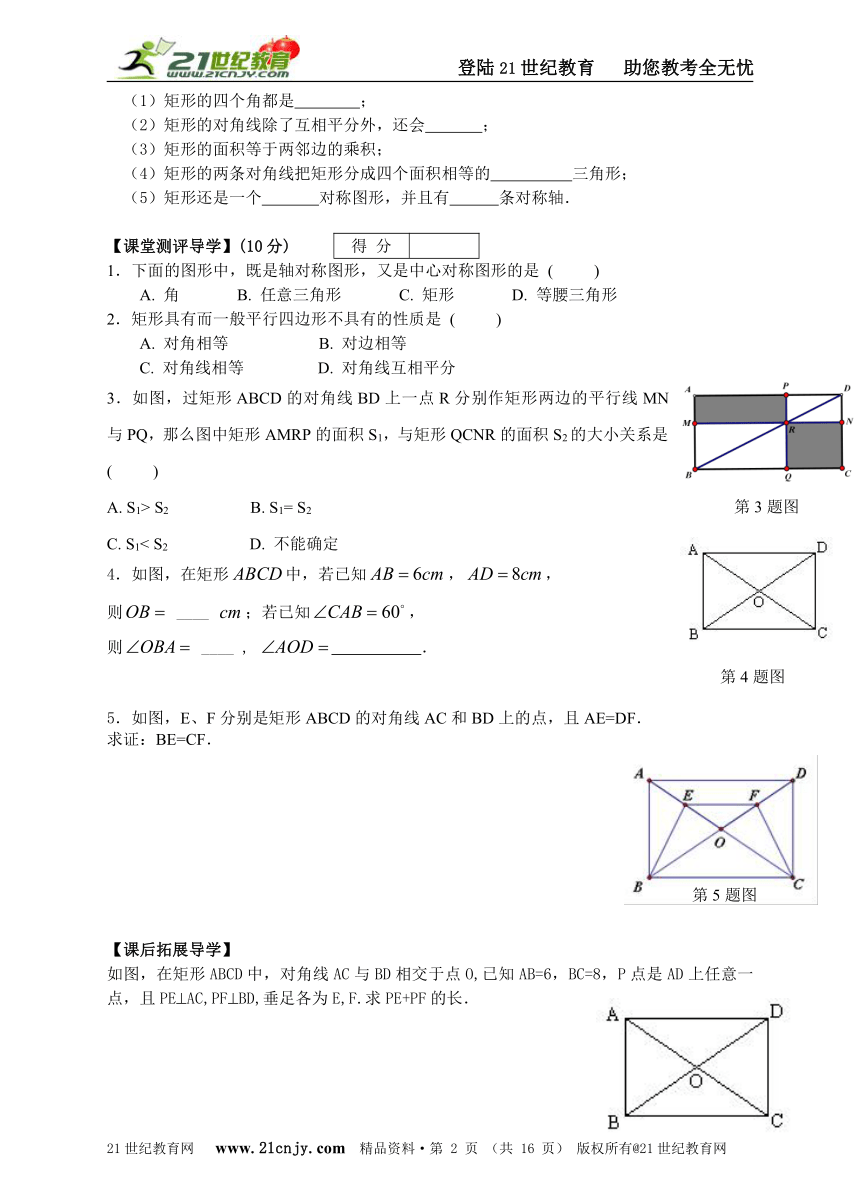
3.如图,过矩形ABCD的对角线BD上一点R分别作矩形两边的平行线MN与PQ,那么图中矩形AMRP的面积S1,与矩形QCNR的面积S2的大小关系是 ( )
A. S1> S2 B. S1= S2
C. S1< S2 D. 不能确定
4.如图,在矩形中,若已知,,
则 ____ ;若已知,
则 ____ , .
5.如图,E、F分别是矩形ABCD的对角线AC和BD上的点,且AE=DF.
求证:BE=CF.
【课后拓展导学】
如图,在矩形ABCD中,对角线AC与BD相交于点O,已知AB=6,BC=8,P点是AD上任意一点,且PE(AC,PF(BD,垂足各为E,F.求PE+PF的长.
5.1矩形(2)
【课前预习导学】
1.判定一个四边形是矩形的方法:
(1)矩形的定义:有一个角是________的_________是矩形;
(2)有三个角是__________的四边形是矩形;
(3)对角线______的__________是矩形.
2.在四边形ABCD中,∠BAD=90°,AB∥CD,请你添上一个条件:_________,使得四边形ABCD是矩形.
3.下列检查一个门框是否为矩形的方法中,正确的是( )
A.测量两条对角线,是否相等
B.测量两条对角线,是否互相平分
C.用曲尺测量门框的三个角,是否都是直角
D.用曲尺测量对角线,是否互相垂直
4.如图,在平行四边形ABCD中,O为边AB的中点,且∠AOD=∠BOC.
求证:平行四边形ABCD是矩形.
【课外资料导学】
矩形纸片的折叠问题的探析
矩形纸片的折叠问题,顾名思义,也就是将矩形纸片按照某种程序折叠,然后,按此程序模拟出平面图形,并按要求完成相应的计算和证明.折叠问题,本质上属于图形的轴对称变换.折叠后的图形与原图形全等,解决这类问题时要抓住因折叠而形成的等线段和等角,这些相等关系是解决问题的关键.这类题目既有趣味性,又有可操作性.学生通过动手实践自主去探索、认识和掌握图形的性质,不仅积累了数学活动的经验,而且还发展了他们的空间观念;另外,还可以培养学生的数学思维能力、运用能力、空间想象能力、解题能力和探究精神.
【课中生成导学】
1.判定矩形方法
定义: 的平行四边形.
定理1: .
定理2: .
2. 四边形、平行四边形、矩形之间的联系.
【课堂测评导学】(10分)
1.在四边形ABCD中,AB=DC,AD=BC.请再添加一个条件,使四边形ABCD是矩形.你添加的条件是 .(写出一种即可)
2.四边形ABCD的对角线交于点O,在下列条件中,不能说明它是矩形的是 ( )
A. AB=CD,AD=BC,∠BAD=90° B.∠BAD=∠ABC =90°,∠BAD+∠ADC=180°
C.∠BAD=∠BCD,∠ABC+∠ADC=180° D. AO=CO,BO=DO,AC=BD
3.如图,在矩形中,,,平分,过点作于,延长、
交于点,下列结论中:①;②;③ ;④,则正确的有( )
A.②③ B.③④
C.①②④ D.②③④
4.如图,将平行四边形ABCD的边DC延长到点E,使CE=CD连接AE,交BC于点F.
求证:△ABF≌△ECF;
∠AFC=2∠D,连接AC.BE,求证四边形ABEC是矩形.
【课后拓展导学】
如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当O点运动到何处时,四边形AECF是矩形?并证明你的结论.
5.2菱形(1)
【课前预习导学】
1.平行四边形的特征:
对边 ;对角 ,邻角 ;对角线 .
2.已知一菱形的周长是24cm,那么这个菱形的边长为 .
3.菱形的边长是2 cm,一条对角线的长是2 cm,则另一条对角线的长是( )
A.4cm B.cm C.2cm D.2cm
4.四边形ABCD是菱形,点O是两条对角线的交点,AB=5cm,AO=4cm,求两条对角线AC和BD的长.
【课外资料导学】
比利时博尔卡特地毯
比利时博尔卡特地毯织造有限公司始创于1955年,是世界著名的仿丝地毯制造商和出口商.博尔卡特利用卓越的传统工艺配合先进的电子织机和不断更新的计算机制图技术,确保产品从花色设计到生产技术更新始终领先世界水平. 博尔卡特拥有严格、完整的质量控制系统,如织厂车间空气始终控制在适当的湿度和温度,以最大限度降低生产过程中的断纱现象. 博尔卡特仿丝地毯抗静电、阻燃、防霉、防蛀,更具有花型细腻、色彩牢固、手感柔软、光泽如丝的特点. 博尔卡特年产地毯超过250万平方米,产品畅销世界各地,而具有菱形图形的地毯是此公司最具特色的款色之一.
【课中生成导学】
1. 菱形的定义: ,此定义可用来判定菱形.
2.菱形具有一般平行四边形都有的性质是:
邻角____________;
对角___________;
对角线________________;
对边_________且_____________.
3.菱形具有一般平行四边形不具有的特殊性质是:
(1)_____________________________________;
(2)_____________________________________.
4. 菱形是特殊的平行四边形,所以它是一个 对称图形,并且还是 对称图形,有 条对称轴.
【课堂测评导学】(10分)
1.菱形具有而一般平行四边形不具有的性质是 ( ) A. 对角相等 B. 对边相等 C. 对角线垂直 D. 对角线互相平分
2.如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于E点,则下列式子不成立的是( )
A.DA=DE B.DB=CE C.∠EAC=90° D.∠ABC=2∠E
3.如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG=(BC﹣AD),⑤四边形EFGH是菱形.其中正确的个数是( )
A.1 B.2 C.3 D.4
4.如图,两个全等菱形的边长为1厘米,一只蚂蚁由点A开始按ABCDEFCGA 的顺序沿菱形的边循环运动,行走2013厘米后停下,则这只蚂蚁停在 点.
5.如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2.
求:(1)∠ABC的度数; (2)对角线AC、BD的长;
(3)菱形ABCD的面积.
【课后拓展导学】
如图,四边形ABCD是菱形,DE⊥AB交BA的延长线于E,DF⊥BC交BC的延长线于F.请你猜想DE与DF的大小有什么关系?并证明你的猜想.
5.2菱形(2)
【课前预习导学】
1.若菱形的边长为4cm,则此菱形的周长是______cm.
2.在菱形ABCD中,若∠ABD=72°,则∠ADC=_______,∠BAD=_______.
3.在菱形ABCD中,若对角线AC=6,BD=8,则CD=_______,此菱形的面积是______.
4.如图,梯形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于点E.求证:四边形AECD是菱形.
【课外资料导学】
半菱形
如图,四边形ABCD中,AB=AD,CB=CD,但AD≠CD,我们称这样的四边形为“半菱形”.小明说:“‘半菱形’的面积等于两条对角线乘积的一半”.他的说法正确吗?请你判断并证明你的结论.
【课中生成导学】
1.判定一个四边形是菱形的方法有:
(1)菱形的定义:有一组邻边______的_______是菱形;
(2)四条边__________的四边形是菱形;
(3)对角线 的_________是菱形.
2.平行四边形、矩形、菱形之间的联系.
【课堂测评导学】(10分)
1.在平行四边形ABCD中添加下列条件,不能判定平行四边形ABCD是菱形的是( )
A.AB=BC B.AC⊥BD C.AC=BD D.∠ABD=∠CBD
2.下列条件中,能判定四边形是菱形的是( )
A.两条对角线相等 B.两条对角线互相垂直
C.两条对角线互相垂直平分 D.两条对角线相等且相互垂直
3.若依次连结四边形各条边的中点所构成的四边形是菱形,则原四边形的对角线一定是 .
4.在直角坐标系中,点A(-1,0),B(1,0),C(0,),若使以点A,B,C,D为顶点的四边形是菱形,则符合条件的点D的个数是 .
5. 如图,在平行四边形中,对角线、相交于点,过点作直线,分别交、于点和.求证:四边形是菱形.
【课后拓展导学】
如图,四边形ABCD是平行四边形,点E,F在直线AB上,且AE=AB=BF,连结CE,DF分别交AD,BC于点M,N.
(1)求证:四边形DMNC是平行四边形;
(2)当AD和MN存在怎样的关系时,四边形DMNC是菱形?请写出此条件,并说明理由.
5.3正方形(1)
【课前预习导学】
1.既是菱形又是矩形的四边形一定是_______________.
2.两条对角线相等的 是正方形,两条对角线互相垂直的 是正方形.
一组邻边相等的 是正方形,有一个内角是直角的 是正方形.
3.下列命题正确的是( )
A.一组对边相等,另一组对边平行的四边形一定是平行四边形;B.对角线相等的四边形一定是矩形;
C.两条对角线互相垂直的四边形一定是菱形;D.两条对角线相等且互相垂直平分的四边形一定是正方形.
4.如图1,在中,,是的中点,, ,垂足分别为.
(1).试说明:; (2).只添加一个条件使四边形是正方形,请你写出至少两种不同的的添加方法(不另外添加辅导线,无须说明理由)
【课外资料导学】
巧移火柴
用16根火柴可以摆成四个大小相同的正方形(图2).如果要减少一根火柴,用15根火柴摆成四个大小相同的正方形,那么只需让图2中的一个正方形与另一个正方形共同使用一根火柴就可以了,于是得到图3的①或②或③.如果用14根火柴摆成四个大小相同的正方形,只需让图2中的两个正方形,具有2根共同使用的火柴就可以了,于是得到图4的①或②.如果用13根火柴摆成四个大小相同的正方形,只需让图2中的三个正方形具有3根共同使用的火柴就可以了,于是得到图5的①或②或③。你能用12根火柴摆成四个大小相同的正方形吗?试一试.
【课中生成导学】
1.正方形与平行四边形、矩形、菱形的包容关系: (名称填在相应的圈内)
2.正方形与 矩形、菱形、平行四边形的关系:(在方框内填入适当的条件使之成立)
得 分
【课堂测评导学】(共10分)
1.在下列命题中,真命题是( )
A.两条对角线相等的四边形是矩形; B.两条对角线互相垂直的四边形是菱形
C.两条对角线互相平分的四边形是平行四边形; D.两条对角线互相垂直且相等的四边形是正方形
2.如图6,如图,将一张长方形纸片对折两次,然后剪下一个角,打开.如果要剪出一个正方形,那么剪口线与折痕成( )
A.角 B.角 C.角 D.角
3.如图7,菱形的对角线相交于点请你添加一个条件: ,使得该菱形为正方形.
4.将一个无盖正方体纸盒展开(如图8①),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图8②).则所剪得的直角三角形较短的与较长的直角边的比是 .
5.(2013?铁岭)如图9,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
【课后拓展导学】
如图(1),把一个长为、宽为的长方形()沿虚线剪开,拼接成图(2),成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为( )
A. B. C. D.
5.3正方形(2)
【课前预习导学】
1.正方形的各边与对角线的夹角为______________度.
2.如图1,四边形是正方形⊿DCE是正三角形.则________.
3.如图2,正方形的边长为1,它的两条对角线相交于点,则⊿ABO的周长为_____,面积为_______
4.如图3,在正方形中,=8,=2, = . 点在上,点在上,则CF=_____
5.如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是 ( )
A. 3∶4 B. 5∶8 C. 9∶16 D. 1∶2
【课外资料导学】
正方形网格图
近几年中考试题中频繁出现了与正方形网格有关的题目,这些题具有创新性、应用性、趣味性和益智性,重在考查我们搜集和处理信息、获取新知识的能力.网格是学生从小就熟悉的图形,在网格中研究格点图形,具有很强的可操作性和较浓的趣味性,真正体现了新课标的“在玩中学,在学中思,在思中得”.
例如: (重庆市)在如图的方格纸中,每个小方格都是边长为1的正方形,点、是方格纸中的两个格点(即正方形的顶点),在这个5×5的方格纸中,找出格点使⊿ABC的面积为2个平方单位,则满足条件的格点的个数是( )
(A)5 (B)4 (C)3 (D)2
【课中生成导学】
1.正方形的一条对角线把正方形分成 个全等的等腰直角三角形,对角线与边的夹角是 ;正方形的两条对角线把它分成 个全等的等腰直角三角形,这是正方形的特殊性质.
2.正方形与平行四边形、矩形、菱形的性质比较:
边
角
对角线
对称性
平行四边形
矩形
菱形
正方形
得 分
【课堂测评导学】(共10分)
1.如图4,每个小正方形的边长为1,,,是小正方形的顶点,则的度数为( )
A. 90° B. 60° C. 45° D. 30°
2.正方形的边长为4,则周长为__,面积为___.
3.如图5,是正方形边上任一点,,交于,于,于,若,则四边形的周长为__________.
4.(2013?嘉兴)如图6,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P与正方形的边碰撞的次数为 ,小球P所经过的路程为 .
5.(2011?江苏南通中考)已知:如图7(1),O为正方形ABCD的中心,分别延长OA到点F,OD到点E,使OF=2OA,OE=2OD,连结EF,将△FOE绕点O逆时针旋转α角得到△(如图7(2)).探究AE′与BF'的数量关系,并给予证明.
【课后拓展导学】
如图8,在正方形中,为上任一点,是的中点,且.
求证:平分
5.1矩形(1)
【课前预习导学】
1.互补 相等 互相平分 平行 相等 2.(1)矩形的四个角都是直角 (2)矩形的对角线相等
3. B 4.
【课中生成导学】
1. 有一个角是直角的平行四边形 2.(1)平行且相等 (2)相等 互补 (3)互相平分 (4)中心
3.(1)直角 (2)相等 (3)等腰 (4)轴 2
【课堂测评导学】
1.C 2.C 3.B 4.5
5.证明:∵四边形ABCD为矩形
∴OA=OB=OC=OD AB=CD
∵AE=DF
∴OE=OF
在ΔBOE与ΔCOF中,
∴ΔBOE≌ΔCOF(SAS)
∴BE=CF
【课后拓展导学】
5.1矩形(2)
【课前预习导学】
1.(1)直角 平行四边形 (2)直角 (3)相等 平行四边形
2.答案不唯一:(如等) 3. C 4. 略
【课中生成导学】
1. 有一个角是直角 2. 有三个角是直角的四边形 3. 对角线相等且互相平分的四边形
【课堂测评导学】
1. 等 2. C 3. D 4. 略
【课后拓展导学】
(1)略 (2)中点
5.2菱形(1)
【课前预习导学】
1.平行且相等 相等 互补 互相平分 2.6cm 3.C 4.AC=8cm BD=6cm
【课中生成导学】
1.一组邻边相等的平行四边形 2.互补 相等 互相垂直且平分 平行 相等
3.(1)菱形的四条边都相等 (2)菱形的对角线互相垂直,并且每条对角线平分一组对角
4.中心 轴 2
【课堂测评导学】
1.C 2.B 3.C 4.F 5. (1) (2) (3)
【课后拓展导学】
DE=DF 证明略
5.2菱形(2)
【课前预习导学】
1.16 2. 3.5 24 4.略
【课中生成导学】
1.(1)相等 平行四边形 (2)都相等 (3)互相平分 平行四边形
【课堂测评导学】
1.C 2.C 3. 互相垂直 4. 3个 5. 略
【课后拓展导学】
(1)略 (2)AD=2MN
5.3正方形(1)
【课前预习导学】
1.正方形 2.菱形 矩形 矩形 菱形 3.
4.提示:(1)连,可知平分 ,由角平分线的性质可得,或全等得到.(2)或或为中点等.
【课中生成导学】
1.略 2.略
【课堂测评导学】
1.C 2.45 3.或等 4.1:2
5.(1)证明:
(2)等腰直角三角形.理由如下:
(已证)
【课后拓展导学】
5.3正方形(2)
【课前预习导学】
1.45 2.30 3. 4. 5. B
【课外资料导学】A
【课中生成导学】
1.2 45° 4
2.正方形与平行四边形、矩形、菱形的性质比较:
边
角
对角线
对称性
平行四边形
对边平行且相等
对角相等,邻角互补
互相平分
中心对称图形
矩形
对边平行且相等
四个角都是直角
相等且互相平分
既是轴对称图形,又是中心对称图形
菱形
对边平行,四边相等
对角相等,邻角互补
互相垂直平分
既是轴对称图形,又是中心对称图形
正方形
对边平行,四边相等
四个角都是直角
相等且互相垂直平分
既是轴对称图形,又是中心对称图形
【课堂测评导学】
1.C 2.16;16cm2 3. 4.6;6
5.AE′=BF 证明:如图2, ∵在正方形ABCD中, AC⊥BD
∴∠=∠AOD=∠AOB=90°即∠AOE′+∠AOF′=∠BOF′+∠AOF′
∴∠AOE′=∠BOF′ 又∵OA=OB=OD,
OE′=2OD,OF′=2OA ∴OE′=OF′ ∴△OAE′≌△OBF′ ∴AE′=BF
【课后拓展导学】
提示:连结MN并延长交AD的延长线于点H. 通过证明⊿MNC≌⊿HND得到DH=CM;再证明AM=AH;最后由等腰三角形三线合一性质即可得到AN平分∠DAM.
5.1矩形(1)
【课前预习导学】
矩形具有一般平行四边形都有的性质是:
邻角____________;
对角___________;
对角线________________;
对边_________且_____________.
2.矩形具有而一般平行四边形不具有的特殊性质是:
(1)_____________________________________.
(2)_____________________________________.
3.已知一矩形的周长是24cm,相邻两边之比是1:2,那么这个矩形的面积是 ( )
A.24cm2 B.32cm2 C.48cm2 D.128cm2
4.如图,在矩形ABCD中,,求这个矩形的周长.
【课外资料导学】
黄金矩形
短边与长边之比为黄金比即0.618的矩形,称作黄金比矩形,也称作黄金率矩形.公元前5世纪的古希腊建筑师已经晓得这种协调性的影响.巴特农神殿就是应用黄金矩形的一个早期建筑的例子.那时的古希腊人已经具有黄金均值及如何作它的知识,还知道如何近似于它以及如何用它来构造黄金矩形.除了影响建筑之外,黄金矩形还出现在艺术中.在公元1509年L·帕西欧里的《神奇的比例》一书中,达·芬奇为人体结构中的黄金均值作了图解.黄金均值用在艺术上是以生动的对称技巧为标志.A·丢勒、G·西雷特、P·曼诸利安、达·芬奇、S·达利、G·贝娄等人,都在他们的一些作品中用黄金矩形去创造富有生气的对称.
【课中生成导学】
1. 矩形的定义: .
2. 矩形是一种特殊的平行四边形,它具有平行四边形的性质,如:
(1)两组对边分别 ; (2)对角 、邻角 ; (3)对角线 ,两条对角线把它分成四个面积相等的三角形; (4)是一个 对称图形.
3. 矩形是一个特殊的平行四边形,它除了具有平行四边形所具备的特征外,还具备一般平行四边形所不具备的特征,如: (1)矩形的四个角都是 ; (2)矩形的对角线除了互相平分外,还会 ; (3)矩形的面积等于两邻边的乘积; (4)矩形的两条对角线把矩形分成四个面积相等的 三角形; (5)矩形还是一个 对称图形,并且有 条对称轴.
【课堂测评导学】(10分)
1.下面的图形中,既是轴对称图形,又是中心对称图形的是 ( ) A. 角 B. 任意三角形 C. 矩形 D. 等腰三角形
2.矩形具有而一般平行四边形不具有的性质是 ( ) A. 对角相等 B. 对边相等 C. 对角线相等 D. 对角线互相平分
3.如图,过矩形ABCD的对角线BD上一点R分别作矩形两边的平行线MN与PQ,那么图中矩形AMRP的面积S1,与矩形QCNR的面积S2的大小关系是 ( )
A. S1> S2 B. S1= S2
C. S1< S2 D. 不能确定
4.如图,在矩形中,若已知,,
则 ____ ;若已知,
则 ____ , .
5.如图,E、F分别是矩形ABCD的对角线AC和BD上的点,且AE=DF.
求证:BE=CF.
【课后拓展导学】
如图,在矩形ABCD中,对角线AC与BD相交于点O,已知AB=6,BC=8,P点是AD上任意一点,且PE(AC,PF(BD,垂足各为E,F.求PE+PF的长.
5.1矩形(2)
【课前预习导学】
1.判定一个四边形是矩形的方法:
(1)矩形的定义:有一个角是________的_________是矩形;
(2)有三个角是__________的四边形是矩形;
(3)对角线______的__________是矩形.
2.在四边形ABCD中,∠BAD=90°,AB∥CD,请你添上一个条件:_________,使得四边形ABCD是矩形.
3.下列检查一个门框是否为矩形的方法中,正确的是( )
A.测量两条对角线,是否相等
B.测量两条对角线,是否互相平分
C.用曲尺测量门框的三个角,是否都是直角
D.用曲尺测量对角线,是否互相垂直
4.如图,在平行四边形ABCD中,O为边AB的中点,且∠AOD=∠BOC.
求证:平行四边形ABCD是矩形.
【课外资料导学】
矩形纸片的折叠问题的探析
矩形纸片的折叠问题,顾名思义,也就是将矩形纸片按照某种程序折叠,然后,按此程序模拟出平面图形,并按要求完成相应的计算和证明.折叠问题,本质上属于图形的轴对称变换.折叠后的图形与原图形全等,解决这类问题时要抓住因折叠而形成的等线段和等角,这些相等关系是解决问题的关键.这类题目既有趣味性,又有可操作性.学生通过动手实践自主去探索、认识和掌握图形的性质,不仅积累了数学活动的经验,而且还发展了他们的空间观念;另外,还可以培养学生的数学思维能力、运用能力、空间想象能力、解题能力和探究精神.
【课中生成导学】
1.判定矩形方法
定义: 的平行四边形.
定理1: .
定理2: .
2. 四边形、平行四边形、矩形之间的联系.
【课堂测评导学】(10分)
1.在四边形ABCD中,AB=DC,AD=BC.请再添加一个条件,使四边形ABCD是矩形.你添加的条件是 .(写出一种即可)
2.四边形ABCD的对角线交于点O,在下列条件中,不能说明它是矩形的是 ( )
A. AB=CD,AD=BC,∠BAD=90° B.∠BAD=∠ABC =90°,∠BAD+∠ADC=180°
C.∠BAD=∠BCD,∠ABC+∠ADC=180° D. AO=CO,BO=DO,AC=BD
3.如图,在矩形中,,,平分,过点作于,延长、
交于点,下列结论中:①;②;③ ;④,则正确的有( )
A.②③ B.③④
C.①②④ D.②③④
4.如图,将平行四边形ABCD的边DC延长到点E,使CE=CD连接AE,交BC于点F.
求证:△ABF≌△ECF;
∠AFC=2∠D,连接AC.BE,求证四边形ABEC是矩形.
【课后拓展导学】
如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:EO=FO;
(2)当O点运动到何处时,四边形AECF是矩形?并证明你的结论.
5.2菱形(1)
【课前预习导学】
1.平行四边形的特征:
对边 ;对角 ,邻角 ;对角线 .
2.已知一菱形的周长是24cm,那么这个菱形的边长为 .
3.菱形的边长是2 cm,一条对角线的长是2 cm,则另一条对角线的长是( )
A.4cm B.cm C.2cm D.2cm
4.四边形ABCD是菱形,点O是两条对角线的交点,AB=5cm,AO=4cm,求两条对角线AC和BD的长.
【课外资料导学】
比利时博尔卡特地毯
比利时博尔卡特地毯织造有限公司始创于1955年,是世界著名的仿丝地毯制造商和出口商.博尔卡特利用卓越的传统工艺配合先进的电子织机和不断更新的计算机制图技术,确保产品从花色设计到生产技术更新始终领先世界水平. 博尔卡特拥有严格、完整的质量控制系统,如织厂车间空气始终控制在适当的湿度和温度,以最大限度降低生产过程中的断纱现象. 博尔卡特仿丝地毯抗静电、阻燃、防霉、防蛀,更具有花型细腻、色彩牢固、手感柔软、光泽如丝的特点. 博尔卡特年产地毯超过250万平方米,产品畅销世界各地,而具有菱形图形的地毯是此公司最具特色的款色之一.
【课中生成导学】
1. 菱形的定义: ,此定义可用来判定菱形.
2.菱形具有一般平行四边形都有的性质是:
邻角____________;
对角___________;
对角线________________;
对边_________且_____________.
3.菱形具有一般平行四边形不具有的特殊性质是:
(1)_____________________________________;
(2)_____________________________________.
4. 菱形是特殊的平行四边形,所以它是一个 对称图形,并且还是 对称图形,有 条对称轴.
【课堂测评导学】(10分)
1.菱形具有而一般平行四边形不具有的性质是 ( ) A. 对角相等 B. 对边相等 C. 对角线垂直 D. 对角线互相平分
2.如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于E点,则下列式子不成立的是( )
A.DA=DE B.DB=CE C.∠EAC=90° D.∠ABC=2∠E
3.如图,E、F、G、H分别是BD、BC、AC、AD的中点,且AB=CD.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG=(BC﹣AD),⑤四边形EFGH是菱形.其中正确的个数是( )
A.1 B.2 C.3 D.4
4.如图,两个全等菱形的边长为1厘米,一只蚂蚁由点A开始按ABCDEFCGA 的顺序沿菱形的边循环运动,行走2013厘米后停下,则这只蚂蚁停在 点.
5.如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2.
求:(1)∠ABC的度数; (2)对角线AC、BD的长;
(3)菱形ABCD的面积.
【课后拓展导学】
如图,四边形ABCD是菱形,DE⊥AB交BA的延长线于E,DF⊥BC交BC的延长线于F.请你猜想DE与DF的大小有什么关系?并证明你的猜想.
5.2菱形(2)
【课前预习导学】
1.若菱形的边长为4cm,则此菱形的周长是______cm.
2.在菱形ABCD中,若∠ABD=72°,则∠ADC=_______,∠BAD=_______.
3.在菱形ABCD中,若对角线AC=6,BD=8,则CD=_______,此菱形的面积是______.
4.如图,梯形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于点E.求证:四边形AECD是菱形.
【课外资料导学】
半菱形
如图,四边形ABCD中,AB=AD,CB=CD,但AD≠CD,我们称这样的四边形为“半菱形”.小明说:“‘半菱形’的面积等于两条对角线乘积的一半”.他的说法正确吗?请你判断并证明你的结论.
【课中生成导学】
1.判定一个四边形是菱形的方法有:
(1)菱形的定义:有一组邻边______的_______是菱形;
(2)四条边__________的四边形是菱形;
(3)对角线 的_________是菱形.
2.平行四边形、矩形、菱形之间的联系.
【课堂测评导学】(10分)
1.在平行四边形ABCD中添加下列条件,不能判定平行四边形ABCD是菱形的是( )
A.AB=BC B.AC⊥BD C.AC=BD D.∠ABD=∠CBD
2.下列条件中,能判定四边形是菱形的是( )
A.两条对角线相等 B.两条对角线互相垂直
C.两条对角线互相垂直平分 D.两条对角线相等且相互垂直
3.若依次连结四边形各条边的中点所构成的四边形是菱形,则原四边形的对角线一定是 .
4.在直角坐标系中,点A(-1,0),B(1,0),C(0,),若使以点A,B,C,D为顶点的四边形是菱形,则符合条件的点D的个数是 .
5. 如图,在平行四边形中,对角线、相交于点,过点作直线,分别交、于点和.求证:四边形是菱形.
【课后拓展导学】
如图,四边形ABCD是平行四边形,点E,F在直线AB上,且AE=AB=BF,连结CE,DF分别交AD,BC于点M,N.
(1)求证:四边形DMNC是平行四边形;
(2)当AD和MN存在怎样的关系时,四边形DMNC是菱形?请写出此条件,并说明理由.
5.3正方形(1)
【课前预习导学】
1.既是菱形又是矩形的四边形一定是_______________.
2.两条对角线相等的 是正方形,两条对角线互相垂直的 是正方形.
一组邻边相等的 是正方形,有一个内角是直角的 是正方形.
3.下列命题正确的是( )
A.一组对边相等,另一组对边平行的四边形一定是平行四边形;B.对角线相等的四边形一定是矩形;
C.两条对角线互相垂直的四边形一定是菱形;D.两条对角线相等且互相垂直平分的四边形一定是正方形.
4.如图1,在中,,是的中点,, ,垂足分别为.
(1).试说明:; (2).只添加一个条件使四边形是正方形,请你写出至少两种不同的的添加方法(不另外添加辅导线,无须说明理由)
【课外资料导学】
巧移火柴
用16根火柴可以摆成四个大小相同的正方形(图2).如果要减少一根火柴,用15根火柴摆成四个大小相同的正方形,那么只需让图2中的一个正方形与另一个正方形共同使用一根火柴就可以了,于是得到图3的①或②或③.如果用14根火柴摆成四个大小相同的正方形,只需让图2中的两个正方形,具有2根共同使用的火柴就可以了,于是得到图4的①或②.如果用13根火柴摆成四个大小相同的正方形,只需让图2中的三个正方形具有3根共同使用的火柴就可以了,于是得到图5的①或②或③。你能用12根火柴摆成四个大小相同的正方形吗?试一试.
【课中生成导学】
1.正方形与平行四边形、矩形、菱形的包容关系: (名称填在相应的圈内)
2.正方形与 矩形、菱形、平行四边形的关系:(在方框内填入适当的条件使之成立)
得 分
【课堂测评导学】(共10分)
1.在下列命题中,真命题是( )
A.两条对角线相等的四边形是矩形; B.两条对角线互相垂直的四边形是菱形
C.两条对角线互相平分的四边形是平行四边形; D.两条对角线互相垂直且相等的四边形是正方形
2.如图6,如图,将一张长方形纸片对折两次,然后剪下一个角,打开.如果要剪出一个正方形,那么剪口线与折痕成( )
A.角 B.角 C.角 D.角
3.如图7,菱形的对角线相交于点请你添加一个条件: ,使得该菱形为正方形.
4.将一个无盖正方体纸盒展开(如图8①),沿虚线剪开,用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图8②).则所剪得的直角三角形较短的与较长的直角边的比是 .
5.(2013?铁岭)如图9,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
【课后拓展导学】
如图(1),把一个长为、宽为的长方形()沿虚线剪开,拼接成图(2),成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为( )
A. B. C. D.
5.3正方形(2)
【课前预习导学】
1.正方形的各边与对角线的夹角为______________度.
2.如图1,四边形是正方形⊿DCE是正三角形.则________.
3.如图2,正方形的边长为1,它的两条对角线相交于点,则⊿ABO的周长为_____,面积为_______
4.如图3,在正方形中,=8,=2, = . 点在上,点在上,则CF=_____
5.如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是 ( )
A. 3∶4 B. 5∶8 C. 9∶16 D. 1∶2
【课外资料导学】
正方形网格图
近几年中考试题中频繁出现了与正方形网格有关的题目,这些题具有创新性、应用性、趣味性和益智性,重在考查我们搜集和处理信息、获取新知识的能力.网格是学生从小就熟悉的图形,在网格中研究格点图形,具有很强的可操作性和较浓的趣味性,真正体现了新课标的“在玩中学,在学中思,在思中得”.
例如: (重庆市)在如图的方格纸中,每个小方格都是边长为1的正方形,点、是方格纸中的两个格点(即正方形的顶点),在这个5×5的方格纸中,找出格点使⊿ABC的面积为2个平方单位,则满足条件的格点的个数是( )
(A)5 (B)4 (C)3 (D)2
【课中生成导学】
1.正方形的一条对角线把正方形分成 个全等的等腰直角三角形,对角线与边的夹角是 ;正方形的两条对角线把它分成 个全等的等腰直角三角形,这是正方形的特殊性质.
2.正方形与平行四边形、矩形、菱形的性质比较:
边
角
对角线
对称性
平行四边形
矩形
菱形
正方形
得 分
【课堂测评导学】(共10分)
1.如图4,每个小正方形的边长为1,,,是小正方形的顶点,则的度数为( )
A. 90° B. 60° C. 45° D. 30°
2.正方形的边长为4,则周长为__,面积为___.
3.如图5,是正方形边上任一点,,交于,于,于,若,则四边形的周长为__________.
4.(2013?嘉兴)如图6,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P与正方形的边碰撞的次数为 ,小球P所经过的路程为 .
5.(2011?江苏南通中考)已知:如图7(1),O为正方形ABCD的中心,分别延长OA到点F,OD到点E,使OF=2OA,OE=2OD,连结EF,将△FOE绕点O逆时针旋转α角得到△(如图7(2)).探究AE′与BF'的数量关系,并给予证明.
【课后拓展导学】
如图8,在正方形中,为上任一点,是的中点,且.
求证:平分
5.1矩形(1)
【课前预习导学】
1.互补 相等 互相平分 平行 相等 2.(1)矩形的四个角都是直角 (2)矩形的对角线相等
3. B 4.
【课中生成导学】
1. 有一个角是直角的平行四边形 2.(1)平行且相等 (2)相等 互补 (3)互相平分 (4)中心
3.(1)直角 (2)相等 (3)等腰 (4)轴 2
【课堂测评导学】
1.C 2.C 3.B 4.5
5.证明:∵四边形ABCD为矩形
∴OA=OB=OC=OD AB=CD
∵AE=DF
∴OE=OF
在ΔBOE与ΔCOF中,
∴ΔBOE≌ΔCOF(SAS)
∴BE=CF
【课后拓展导学】
5.1矩形(2)
【课前预习导学】
1.(1)直角 平行四边形 (2)直角 (3)相等 平行四边形
2.答案不唯一:(如等) 3. C 4. 略
【课中生成导学】
1. 有一个角是直角 2. 有三个角是直角的四边形 3. 对角线相等且互相平分的四边形
【课堂测评导学】
1. 等 2. C 3. D 4. 略
【课后拓展导学】
(1)略 (2)中点
5.2菱形(1)
【课前预习导学】
1.平行且相等 相等 互补 互相平分 2.6cm 3.C 4.AC=8cm BD=6cm
【课中生成导学】
1.一组邻边相等的平行四边形 2.互补 相等 互相垂直且平分 平行 相等
3.(1)菱形的四条边都相等 (2)菱形的对角线互相垂直,并且每条对角线平分一组对角
4.中心 轴 2
【课堂测评导学】
1.C 2.B 3.C 4.F 5. (1) (2) (3)
【课后拓展导学】
DE=DF 证明略
5.2菱形(2)
【课前预习导学】
1.16 2. 3.5 24 4.略
【课中生成导学】
1.(1)相等 平行四边形 (2)都相等 (3)互相平分 平行四边形
【课堂测评导学】
1.C 2.C 3. 互相垂直 4. 3个 5. 略
【课后拓展导学】
(1)略 (2)AD=2MN
5.3正方形(1)
【课前预习导学】
1.正方形 2.菱形 矩形 矩形 菱形 3.
4.提示:(1)连,可知平分 ,由角平分线的性质可得,或全等得到.(2)或或为中点等.
【课中生成导学】
1.略 2.略
【课堂测评导学】
1.C 2.45 3.或等 4.1:2
5.(1)证明:
(2)等腰直角三角形.理由如下:
(已证)
【课后拓展导学】
5.3正方形(2)
【课前预习导学】
1.45 2.30 3. 4. 5. B
【课外资料导学】A
【课中生成导学】
1.2 45° 4
2.正方形与平行四边形、矩形、菱形的性质比较:
边
角
对角线
对称性
平行四边形
对边平行且相等
对角相等,邻角互补
互相平分
中心对称图形
矩形
对边平行且相等
四个角都是直角
相等且互相平分
既是轴对称图形,又是中心对称图形
菱形
对边平行,四边相等
对角相等,邻角互补
互相垂直平分
既是轴对称图形,又是中心对称图形
正方形
对边平行,四边相等
四个角都是直角
相等且互相垂直平分
既是轴对称图形,又是中心对称图形
【课堂测评导学】
1.C 2.16;16cm2 3. 4.6;6
5.AE′=BF 证明:如图2, ∵在正方形ABCD中, AC⊥BD
∴∠=∠AOD=∠AOB=90°即∠AOE′+∠AOF′=∠BOF′+∠AOF′
∴∠AOE′=∠BOF′ 又∵OA=OB=OD,
OE′=2OD,OF′=2OA ∴OE′=OF′ ∴△OAE′≌△OBF′ ∴AE′=BF
【课后拓展导学】
提示:连结MN并延长交AD的延长线于点H. 通过证明⊿MNC≌⊿HND得到DH=CM;再证明AM=AH;最后由等腰三角形三线合一性质即可得到AN平分∠DAM.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
