浙教版数学七年级上册 1.2 数轴 (共31张PPT)
文档属性
| 名称 | 浙教版数学七年级上册 1.2 数轴 (共31张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-19 00:00:00 | ||
图片预览







文档简介
(共31张PPT)
浙教版义务教育教科书 七年级上册
1.2 数轴
1、按整数和分数将有理数进行分类:
有理数
正整数
正分数
负分数
整数
分数
零
负整数
自然数
复习回顾
一
2、按正负性将有理数进行分类:
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
复习回顾
一
B
观察如图所示的温度计,回答下列问题:
(1)点A表示多少摄氏度?点B呢?点C呢?
(2)A、B、C三点所表示的温度哪个高哪个低?
A
C
情境引入
一
①以0为基准
②两条刻度线间距离相等
③0以上为正数,0以下为负数
……
(3)温度计上的刻度有什么特点?
0
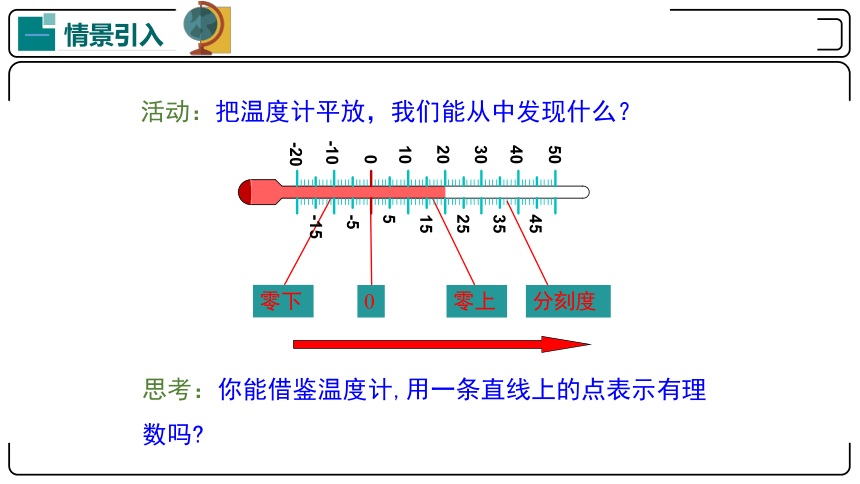
活动:把温度计平放,我们能从中发现什么?
零下
零上
分刻度
思考:你能借鉴温度计,用一条直线上的点表示有理数吗
情景引入
一
画一条水平直线,在直线上取一点表示0,并把这个点叫作原点,选取某一长度作为单位长度,规定直线上向右的方向为正方向,就得到下面的数轴.
数轴的概念
一
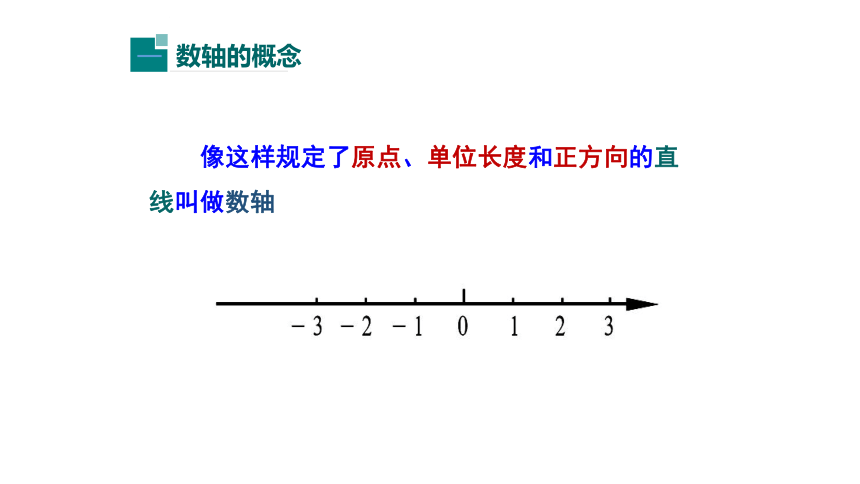
像这样规定了原点、单位长度和正方向的直线叫做数轴
数轴的概念
一
1.画直线定原点(如图),0表示原点.
0
2.定正方向
通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
3.定单位长度,选择适当的长度为单位长度,并且统一.
0
0
1
2
3
-1
-2
-3
数轴的画法
一
数轴的三要素
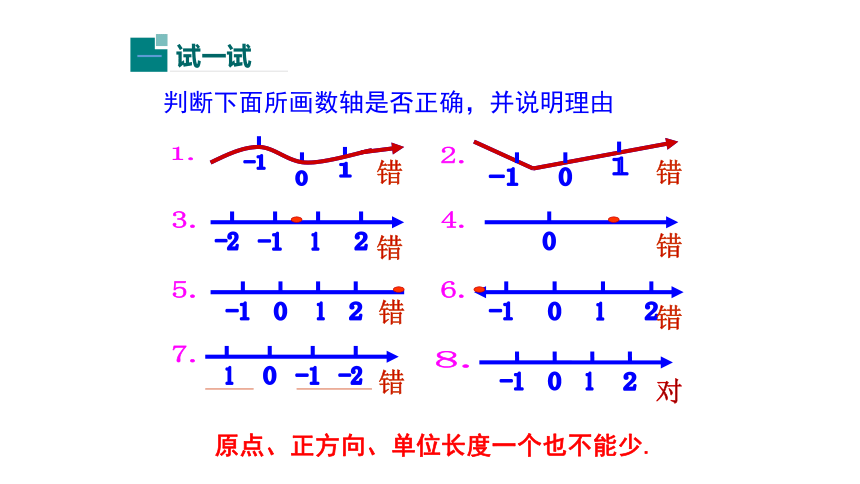
原点、正方向、单位长度一个也不能少.
判断下面所画数轴是否正确,并说明理由
试一试
一
下列图形哪些是数轴,哪些不是,为什么?
(E)
(F)
(D)
再强化概念,深入理解
(A)
(C)
(B)
在数轴上的有理数
二
例1、如图,数轴上的点A,B,C,D分别表示什么数?
解:点A表示-5,点B表示-1,点C表示0,点D表示3.5.
0
—3 —2 —1 1 2 3
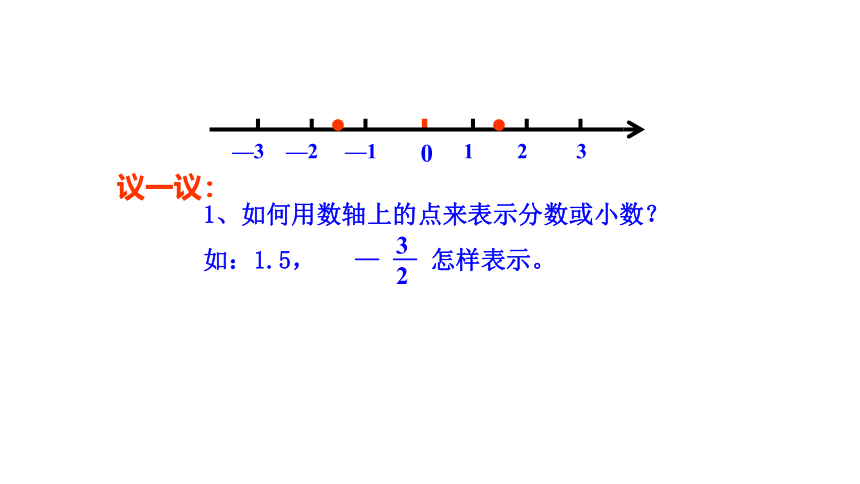
1、如何用数轴上的点来表示分数或小数?
如:1.5, — — 怎样表示。
议一议:
2
3
.
.
有理数
二
正有理数在数轴上用原点右边的点表示
负有理数在数轴上用原点左边的点表示
0用原点表示
在数轴上画表示有理数的点时,要画出实心的小圆点
有理数都可以用数轴上的点表示,但数轴上的点表示的不都是有理数
例2:在所给数轴上画出表示下列各数的点。
1,-5,-2.5, 4 , 0
-5 -4 -3 -2 -1 0 1 2 3 4 5
解:
1
-5
4
●
●
●
●
●
-2.5
0
注意:
①把点标在线上;
②把数标在点的上方, 以便观看。
思考:
请同学们开动你的脑筋想一想,我们选择什么的数轴,能标出 1000,5000,-2000,-4000的大数呢
注意:对很大(或很小)的数,我们要选适当的单位长度确定数轴再在数轴上标出所求的大数(或很小)的数
在数轴上表示有理数
二
书上例2、在数轴上表示下列各数:
(1)0.5,- ,0,-4, ,-0.5,1,4;
(2)200,-150,-50,100,-100 .
解:(1)如图所示:
(2)如图所示:
相反数
二
-4和4有什么相同与不同之处?它们在数轴上的位置有什么关系?
与 呢? -0.5与0.5呢?
相反数
二
如果两个数只有符号不同,那么我们称其中一个数为另一个数的相反数,也称这两个数互为相反数.
相反数是两数之间的一种关系
注意:(1)0的相反数是0;
(2)a的相反数是-a.
在数轴上,表示互为相反数(零除外)的两个点,位于原点的两侧,并且到原点的距离相等.
几何意义
辨一辨
二
①数轴上的点只能表示整数
②数轴上的点所表示的数都是有理数
③数轴上原点表示的数是零
④数轴上的点所表示的数不是正数就是负数
⑤-a不一定是负数
⑥符号相反的两个数互为相反数
×
×
×
×
√
√
想 一 想
(1)怎样求一个数的相反数?
(4)当字母 a 表示 一个有理数时 ,
+a一定是正数吗? -a一定是负数吗?
(3)分别解释 +a, -a,+( -a),
-( -a)所表示的意义。
(2)分别解释 +2 , -2 ,+( -2),
-( -2)所表示的意义。
强化概念,深入理解
1.分别写出下列数的相反数。
5, 2.6, 3/7, 19%
练习:
-3, -0.7, -1/2, -30%
0
我们看到,
一个正数的相反数是一个负数,
一个负数的相反数是一个正数,
0的相反数是0
2. 化简下列各数:
(1) -(+3); (2) -(-2);
(3) -[-(-5)]; (4) -[-(+5)];
(5) -(-m); (6) +(-a);
(7) -(a-b); (8) -(a+b).
= -3
= 2
= -5
= 5
= m
= -a
= -a+b
= -a-b
3.(1)如果数轴上的两点A , B所表示的数互为
相反数,点A在原点的左侧,并且A,B
之间的距离是8 ,那么点B 所表示 的数
是 。
(2) 若a = -72时,则-a = 。
若-x = - 63时,则 x = 。
(3) 若a + 4 = 0 , 则 a = 。
4
72
63
-4
互为相反数的两个数,和为0,即:
若a、b互为相反数,则a+b=0.
4.从数轴上表示-1的点出发,向左移动两个单位长度到点B,则点B表示的数是 ,再向右移动5个单位长度到达点C,则点C表示的数是 .
0
-3 -2 -1 1 2 3
C
.
.
左移2个
右移5个
.
B
-3
2
这节课学到了什么?
1、数轴的三要素:
原点、单位长度、正方向;
2、任何一个有理数都可以用数轴上的点表示;
3、相反数的概念;
零的相反数是零。
4、互为相反数的(零除外)的两个点在数轴上的位置关系:
位于原点的两侧,并且到原点的距离相等。
课堂总结
5、常用的数学思想方法:(1)数形结合,(2)分类讨论
课堂小结
这节课学到了什么?
1、数轴的三要素:
原点、单位长度、正方向;
2、任何一个有理数都可以用数轴上的点表示;
3、相反数的概念;
零的相反数是零。
4、互为相反数的(零除外)的两个点在数轴上的位置关系:
位于原点的两侧,并且到原点的距离相等。
5、常用的数学思想方法:(1)数形结合,(2)分类讨论
点A为数轴上表示-2的动点,当点A沿数轴移动4个单位长度到点B时,点B所表示的数为 ( )
A.2 B.-6
C.2或-6 D.不同于以上
拓展训练
C
分析:点A可能向左移,也可能向右移,所以需分情况讨论.
拓展训练
C
数轴上表示整数的点称为整点。某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2004厘米的线段AB,则线段AB盖住的整点的个数是( )
A. 2002或2003 B. 2003或2004
C. 2004或2005 D. 2005或2006
当堂练习
C
1.下列说法中正确的是( )
A. 在数轴上的点表示的数不是正数就是负数
B.数轴的长度是有限的
C. 一个有理数总可以在数轴上找到一个表示它的点
D. 所有整数都可以用数轴上的点表示,但分数就不一定能找到表示它的点
2.与原点距离是2.5个单位长度的点所表示的有理数是( )
A.2.5 B.-2.5
C.±2.5 D.这个数无法确定
3.在数轴上表示数6的点在原点_____侧,到原点的距离是_____个单位长度,表示数-8的点在原点的_____侧,到原点的距离是_____个单位长度.表示数6的点
到表示数-8的点的距离是______个单位长度.
4.在数轴上到表示-2的点相距8个单位长度的点表示的数为________.
C
右
6
左
8
14
-10或6
5. 画出数轴并表示下列有理数:
1.5,-2.2,-2.5, , ,0.
-3 -2 -1 0 1 2 3 4 5
●
●
1.5
●
-2.2
●
-2.5
●
●
浙教版义务教育教科书 七年级上册
1.2 数轴
1、按整数和分数将有理数进行分类:
有理数
正整数
正分数
负分数
整数
分数
零
负整数
自然数
复习回顾
一
2、按正负性将有理数进行分类:
有理数
正整数
负整数
负分数
正有理数
负有理数
正分数
零
复习回顾
一
B
观察如图所示的温度计,回答下列问题:
(1)点A表示多少摄氏度?点B呢?点C呢?
(2)A、B、C三点所表示的温度哪个高哪个低?
A
C
情境引入
一
①以0为基准
②两条刻度线间距离相等
③0以上为正数,0以下为负数
……
(3)温度计上的刻度有什么特点?
0
活动:把温度计平放,我们能从中发现什么?
零下
零上
分刻度
思考:你能借鉴温度计,用一条直线上的点表示有理数吗
情景引入
一
画一条水平直线,在直线上取一点表示0,并把这个点叫作原点,选取某一长度作为单位长度,规定直线上向右的方向为正方向,就得到下面的数轴.
数轴的概念
一
像这样规定了原点、单位长度和正方向的直线叫做数轴
数轴的概念
一
1.画直线定原点(如图),0表示原点.
0
2.定正方向
通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
3.定单位长度,选择适当的长度为单位长度,并且统一.
0
0
1
2
3
-1
-2
-3
数轴的画法
一
数轴的三要素
原点、正方向、单位长度一个也不能少.
判断下面所画数轴是否正确,并说明理由
试一试
一
下列图形哪些是数轴,哪些不是,为什么?
(E)
(F)
(D)
再强化概念,深入理解
(A)
(C)
(B)
在数轴上的有理数
二
例1、如图,数轴上的点A,B,C,D分别表示什么数?
解:点A表示-5,点B表示-1,点C表示0,点D表示3.5.
0
—3 —2 —1 1 2 3
1、如何用数轴上的点来表示分数或小数?
如:1.5, — — 怎样表示。
议一议:
2
3
.
.
有理数
二
正有理数在数轴上用原点右边的点表示
负有理数在数轴上用原点左边的点表示
0用原点表示
在数轴上画表示有理数的点时,要画出实心的小圆点
有理数都可以用数轴上的点表示,但数轴上的点表示的不都是有理数
例2:在所给数轴上画出表示下列各数的点。
1,-5,-2.5, 4 , 0
-5 -4 -3 -2 -1 0 1 2 3 4 5
解:
1
-5
4
●
●
●
●
●
-2.5
0
注意:
①把点标在线上;
②把数标在点的上方, 以便观看。
思考:
请同学们开动你的脑筋想一想,我们选择什么的数轴,能标出 1000,5000,-2000,-4000的大数呢
注意:对很大(或很小)的数,我们要选适当的单位长度确定数轴再在数轴上标出所求的大数(或很小)的数
在数轴上表示有理数
二
书上例2、在数轴上表示下列各数:
(1)0.5,- ,0,-4, ,-0.5,1,4;
(2)200,-150,-50,100,-100 .
解:(1)如图所示:
(2)如图所示:
相反数
二
-4和4有什么相同与不同之处?它们在数轴上的位置有什么关系?
与 呢? -0.5与0.5呢?
相反数
二
如果两个数只有符号不同,那么我们称其中一个数为另一个数的相反数,也称这两个数互为相反数.
相反数是两数之间的一种关系
注意:(1)0的相反数是0;
(2)a的相反数是-a.
在数轴上,表示互为相反数(零除外)的两个点,位于原点的两侧,并且到原点的距离相等.
几何意义
辨一辨
二
①数轴上的点只能表示整数
②数轴上的点所表示的数都是有理数
③数轴上原点表示的数是零
④数轴上的点所表示的数不是正数就是负数
⑤-a不一定是负数
⑥符号相反的两个数互为相反数
×
×
×
×
√
√
想 一 想
(1)怎样求一个数的相反数?
(4)当字母 a 表示 一个有理数时 ,
+a一定是正数吗? -a一定是负数吗?
(3)分别解释 +a, -a,+( -a),
-( -a)所表示的意义。
(2)分别解释 +2 , -2 ,+( -2),
-( -2)所表示的意义。
强化概念,深入理解
1.分别写出下列数的相反数。
5, 2.6, 3/7, 19%
练习:
-3, -0.7, -1/2, -30%
0
我们看到,
一个正数的相反数是一个负数,
一个负数的相反数是一个正数,
0的相反数是0
2. 化简下列各数:
(1) -(+3); (2) -(-2);
(3) -[-(-5)]; (4) -[-(+5)];
(5) -(-m); (6) +(-a);
(7) -(a-b); (8) -(a+b).
= -3
= 2
= -5
= 5
= m
= -a
= -a+b
= -a-b
3.(1)如果数轴上的两点A , B所表示的数互为
相反数,点A在原点的左侧,并且A,B
之间的距离是8 ,那么点B 所表示 的数
是 。
(2) 若a = -72时,则-a = 。
若-x = - 63时,则 x = 。
(3) 若a + 4 = 0 , 则 a = 。
4
72
63
-4
互为相反数的两个数,和为0,即:
若a、b互为相反数,则a+b=0.
4.从数轴上表示-1的点出发,向左移动两个单位长度到点B,则点B表示的数是 ,再向右移动5个单位长度到达点C,则点C表示的数是 .
0
-3 -2 -1 1 2 3
C
.
.
左移2个
右移5个
.
B
-3
2
这节课学到了什么?
1、数轴的三要素:
原点、单位长度、正方向;
2、任何一个有理数都可以用数轴上的点表示;
3、相反数的概念;
零的相反数是零。
4、互为相反数的(零除外)的两个点在数轴上的位置关系:
位于原点的两侧,并且到原点的距离相等。
课堂总结
5、常用的数学思想方法:(1)数形结合,(2)分类讨论
课堂小结
这节课学到了什么?
1、数轴的三要素:
原点、单位长度、正方向;
2、任何一个有理数都可以用数轴上的点表示;
3、相反数的概念;
零的相反数是零。
4、互为相反数的(零除外)的两个点在数轴上的位置关系:
位于原点的两侧,并且到原点的距离相等。
5、常用的数学思想方法:(1)数形结合,(2)分类讨论
点A为数轴上表示-2的动点,当点A沿数轴移动4个单位长度到点B时,点B所表示的数为 ( )
A.2 B.-6
C.2或-6 D.不同于以上
拓展训练
C
分析:点A可能向左移,也可能向右移,所以需分情况讨论.
拓展训练
C
数轴上表示整数的点称为整点。某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2004厘米的线段AB,则线段AB盖住的整点的个数是( )
A. 2002或2003 B. 2003或2004
C. 2004或2005 D. 2005或2006
当堂练习
C
1.下列说法中正确的是( )
A. 在数轴上的点表示的数不是正数就是负数
B.数轴的长度是有限的
C. 一个有理数总可以在数轴上找到一个表示它的点
D. 所有整数都可以用数轴上的点表示,但分数就不一定能找到表示它的点
2.与原点距离是2.5个单位长度的点所表示的有理数是( )
A.2.5 B.-2.5
C.±2.5 D.这个数无法确定
3.在数轴上表示数6的点在原点_____侧,到原点的距离是_____个单位长度,表示数-8的点在原点的_____侧,到原点的距离是_____个单位长度.表示数6的点
到表示数-8的点的距离是______个单位长度.
4.在数轴上到表示-2的点相距8个单位长度的点表示的数为________.
C
右
6
左
8
14
-10或6
5. 画出数轴并表示下列有理数:
1.5,-2.2,-2.5, , ,0.
-3 -2 -1 0 1 2 3 4 5
●
●
1.5
●
-2.2
●
-2.5
●
●
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
