浙教版数学七年级上册 1.3 绝对值 课件(共18张PPT)
文档属性
| 名称 | 浙教版数学七年级上册 1.3 绝对值 课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-01-19 21:31:53 | ||
图片预览






文档简介
(共18张PPT)
浙教版义务教育教科书 七年级上册
1.3 绝对值
复习回顾
一
1、什么叫做数轴?
规定了原点、正方向、单位长度的直线叫做数轴.
2、什么叫做相反数?
只有符号不同的两个数,叫做互为相反数,
a的相反数是-a.
3、若a,b两数互为相反数,则a+b=_____
0
4、相反数是它本身的数是_____
0
情景引入
一
两位同学在书店购买书籍后回家,一位同学乘上甲出租车向东行驶10千米到达A处,另一位同学乘上乙出租车向西行驶10千米到达B处.两位同学所付的出租车钱一样吗 为什么
一样,因为两人所走的路程相同
出租车按行驶的里程收费,与行驶的路线、方向无关
合作学习
一
(1)甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正.两辆出租车都从O地出发,甲车向东行驶 6 km到达A处,记______km,乙车向西行驶 6 km到达B处,记做_______km.
以O为原点,取适当的单位长度画数轴,并在数轴上标出A、B的位置,则A、B两点与原点距离分别是多少?它们的实际意义是什么?
+6
-6
绝对值
一
定义:一个数在数轴上对应的点到原点的距离叫做这个数的绝对值
记法:若用a表示一个数,a的绝对值记做 a .
读法:a的绝对值.
性质:| a |≥0 (非负性)
绝对值
一
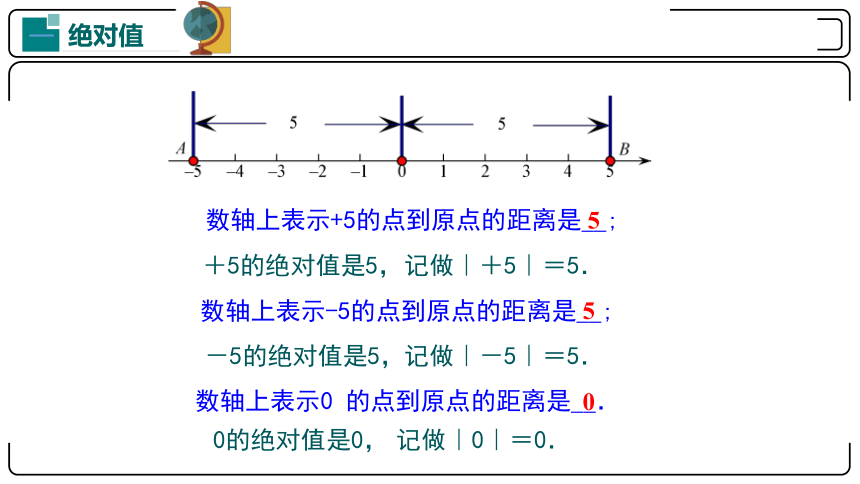
数轴上表示+5的点到原点的距离是__;
数轴上表示-5的点到原点的距离是__;
数轴上表示0 的点到原点的距离是__.
+5的绝对值是5,
记做|+5|=5.
-5的绝对值是5,
记做|-5|=5.
0的绝对值是0,
记做|0|=0.
5
5
0
例1
一
求下列各数的绝对值
思考:一个数的绝对值与这个数有什么关系?
绝对值
一
1.正数的绝对值是________
2.负数的绝对值是____________
3.0的绝对值是____
| a | =
( a > 0 )
a
( a = 0 )
0
( a < 0 )
-a
它本身
它的相反数
0
练习巩固
一
求下列各数的绝对值:
解:
例2
一
求绝对值等于4的数.
+4和-4.
如果一个数的绝对值是一个正数,那么这个数有两个,它们是互为相反数.即:
若a>0,|x|=a,则x=±a.
1、绝对值等于3的数有 _________个,它们是_________。
2、若│x│=4,则x=______,若│x-5│=0,则x=_________.
3、已知|x|=3,|y|=4,求x+y的值。
练习巩固
一
2
互为相反数
练习巩固
一
1.去绝对值化简:
=9
=-8
=15
=???
练习巩固
一
2.计算:
解:(1)原式=9+1
=10
(2)|-10|-|-8|
=10-8
=2
绝对值
一
相反数 绝对值
21
0
填一填
-21
0
21
0
思考:从表格中你发现了什么?
互为相反数的两个数的绝对值相等
如果两个数的绝对值相等,那么这两个数的关系是 .
相等或互为相反数
拓展提高
一
(1)写出绝对值大于2小于6的所有整数______
(2)绝对值小于2011的所有整数的和是______
拓展提高
一
已知a,b是有理数,且|a-1|+|b-2|=0,求a,b的值
非负性 │a│≥0
拓展提高
一
时钟报时的准确程度是衡量时钟质量的一个重要方面,某检测员对A,B,C,D,E五个时钟进行准确性测试,记录了如下数据(记一昼夜后比标准时间早为正,慢为负,单位:秒):
A
B
C
D
E
-10
+3
+5
-1
-7
仅从报时的准确程度来考虑,哪个时钟的质量好一些
课堂小结
1.有理数的绝对值的意义.
代数意义:一个正数的绝对值是 ;
零的绝对值是 ;
一个负数的绝对值是 .
几何意义:表示到原点的距离
2.绝对值的性质:
3.绝对值与相反数的关系:
|a|≥0(非负性)
互为相反数的两个数的绝对值 ;
绝对值相等,符号相反的两个数 ;
若|a|=|b|,则
4.绝对值等于本身的数:
5.绝对值为非零数,则原数有
0和正数(非负数)
2个,且互为相反数
它本身
零
它的相反数
相等
互为相反数
a=b或者a=-b
浙教版义务教育教科书 七年级上册
1.3 绝对值
复习回顾
一
1、什么叫做数轴?
规定了原点、正方向、单位长度的直线叫做数轴.
2、什么叫做相反数?
只有符号不同的两个数,叫做互为相反数,
a的相反数是-a.
3、若a,b两数互为相反数,则a+b=_____
0
4、相反数是它本身的数是_____
0
情景引入
一
两位同学在书店购买书籍后回家,一位同学乘上甲出租车向东行驶10千米到达A处,另一位同学乘上乙出租车向西行驶10千米到达B处.两位同学所付的出租车钱一样吗 为什么
一样,因为两人所走的路程相同
出租车按行驶的里程收费,与行驶的路线、方向无关
合作学习
一
(1)甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程数为正.两辆出租车都从O地出发,甲车向东行驶 6 km到达A处,记______km,乙车向西行驶 6 km到达B处,记做_______km.
以O为原点,取适当的单位长度画数轴,并在数轴上标出A、B的位置,则A、B两点与原点距离分别是多少?它们的实际意义是什么?
+6
-6
绝对值
一
定义:一个数在数轴上对应的点到原点的距离叫做这个数的绝对值
记法:若用a表示一个数,a的绝对值记做 a .
读法:a的绝对值.
性质:| a |≥0 (非负性)
绝对值
一
数轴上表示+5的点到原点的距离是__;
数轴上表示-5的点到原点的距离是__;
数轴上表示0 的点到原点的距离是__.
+5的绝对值是5,
记做|+5|=5.
-5的绝对值是5,
记做|-5|=5.
0的绝对值是0,
记做|0|=0.
5
5
0
例1
一
求下列各数的绝对值
思考:一个数的绝对值与这个数有什么关系?
绝对值
一
1.正数的绝对值是________
2.负数的绝对值是____________
3.0的绝对值是____
| a | =
( a > 0 )
a
( a = 0 )
0
( a < 0 )
-a
它本身
它的相反数
0
练习巩固
一
求下列各数的绝对值:
解:
例2
一
求绝对值等于4的数.
+4和-4.
如果一个数的绝对值是一个正数,那么这个数有两个,它们是互为相反数.即:
若a>0,|x|=a,则x=±a.
1、绝对值等于3的数有 _________个,它们是_________。
2、若│x│=4,则x=______,若│x-5│=0,则x=_________.
3、已知|x|=3,|y|=4,求x+y的值。
练习巩固
一
2
互为相反数
练习巩固
一
1.去绝对值化简:
=9
=-8
=15
=???
练习巩固
一
2.计算:
解:(1)原式=9+1
=10
(2)|-10|-|-8|
=10-8
=2
绝对值
一
相反数 绝对值
21
0
填一填
-21
0
21
0
思考:从表格中你发现了什么?
互为相反数的两个数的绝对值相等
如果两个数的绝对值相等,那么这两个数的关系是 .
相等或互为相反数
拓展提高
一
(1)写出绝对值大于2小于6的所有整数______
(2)绝对值小于2011的所有整数的和是______
拓展提高
一
已知a,b是有理数,且|a-1|+|b-2|=0,求a,b的值
非负性 │a│≥0
拓展提高
一
时钟报时的准确程度是衡量时钟质量的一个重要方面,某检测员对A,B,C,D,E五个时钟进行准确性测试,记录了如下数据(记一昼夜后比标准时间早为正,慢为负,单位:秒):
A
B
C
D
E
-10
+3
+5
-1
-7
仅从报时的准确程度来考虑,哪个时钟的质量好一些
课堂小结
1.有理数的绝对值的意义.
代数意义:一个正数的绝对值是 ;
零的绝对值是 ;
一个负数的绝对值是 .
几何意义:表示到原点的距离
2.绝对值的性质:
3.绝对值与相反数的关系:
|a|≥0(非负性)
互为相反数的两个数的绝对值 ;
绝对值相等,符号相反的两个数 ;
若|a|=|b|,则
4.绝对值等于本身的数:
5.绝对值为非零数,则原数有
0和正数(非负数)
2个,且互为相反数
它本身
零
它的相反数
相等
互为相反数
a=b或者a=-b
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
