2.1 一元二次方程(1)

课件24张PPT。泰顺六中 翁怀新2014年3月5日2.1一元二次方程（1）什么是方程？什么是方程的解（或根）？答：含有未知数的等式叫做方程。使方程两边成立的未知数的值叫做方程的解。曾学过哪些方程？一元一次方程，二元一次方程(组)。什么叫做一元一次方程？温故知新方程的两边都是整式，只含有一个未知数；并且未知数的指数是一次，这样的方程叫做
一元一次方程
含有两个未知数,且含未知数的项的次数都是 一次的方程叫做二元一次方程.由两个一次方程组成，并且含有两个未知数的方程组，叫做二元一次方程组.
1、有一棵树，刚移栽时，树高为2m，假设以后平均每年长0.3m，几年后树高为5m？
设x年后树高为5m，
可列出方程 。0.3x+2=5根据题意列方程解：设这块铁片的宽为x cm，那么它的长
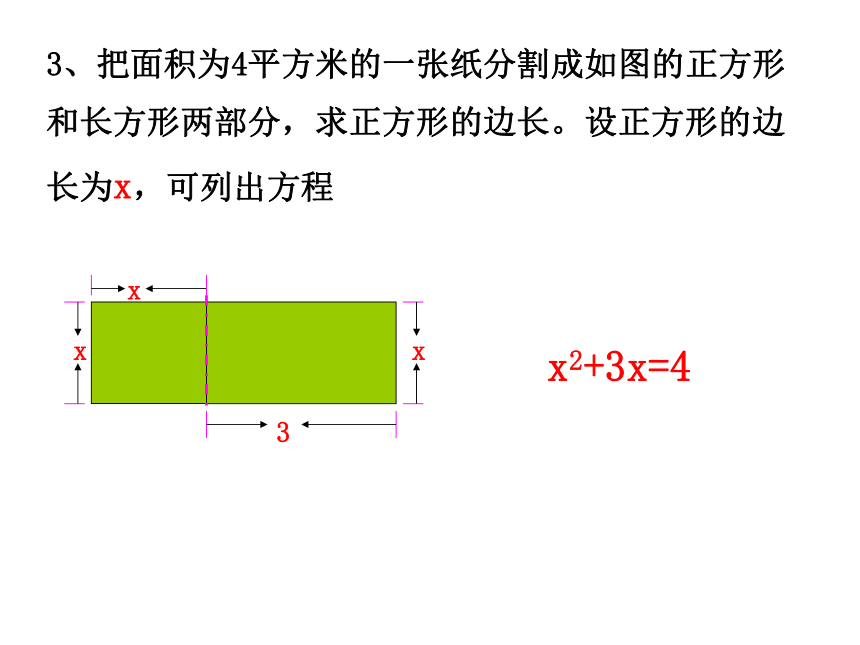
为（x+5) cm. 根据题意，得x（x+5)=150. 去括号，得 x2+5x=150.2、剪一块面积为150cm2的长方形铁片，使它的长比宽多5cm，这块铁片应怎样剪？根据题意列方程3、把面积为4平方米的一张纸分割成如图的正方形和长方形两部分，求正方形的边长。设正方形的边长为x，可列出方程 xx2+3x=4问:这两个有什么相同的特点?即共同点:(1)两边都是整式;
(2)只含有一个未知数;
(3)未知数最高次数为2次观察所列方程具有以上三个特点的方程称为一元二次方程（②x2+5x=150方程（2） x2+5x=150和.③x2+3x=4的两边都是整式，并且只含有一个未知数，并且未知数最高次数为2次我们把这样的方程叫做一元二次方程③x2+3x=4
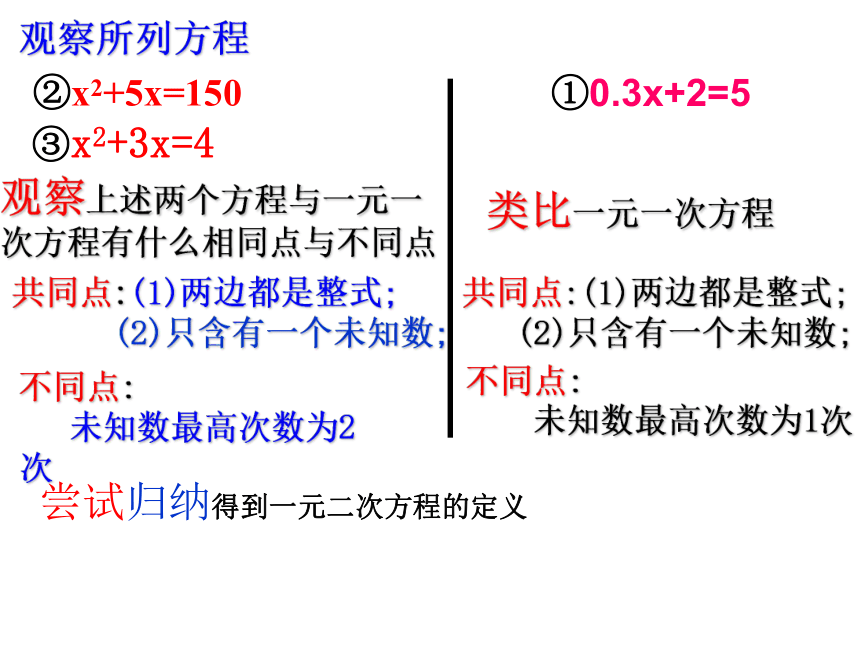
①0.3x+2=5③x2+3x=4 ②x2+5x=150观察所列方程观察上述两个方程与一元一次方程有什么相同点与不同点类比一元一次方程共同点:(1)两边都是整式;
(2)只含有一个未知数;共同点:(1)两边都是整式;
(2)只含有一个未知数;不同点:
未知数最高次数为2次
不同点:
未知数最高次数为1次
尝试归纳得到一元二次方程的定义判断下列方程是否为一元二次方程：① 10x2=9 ( ) ②2(x-1)=3x ( )
③2x2-3x-1=0 ( ) ( )
⑤2xy-7=0 ( ) ⑥9x2=5-4x ( )
⑦4x2=5x ( ) ⑧3y2+4=5y ( ) √√√√×××√ 其中ax2,bx,c分别称为二次项，一次项，常数项，a,b分别称为二次项系数,一次项系数.判断下列方程是一元二次方程吗?√√√√√ ax2 + bx + c = 0注意:要确定一元二次方程的系数和常数项 ,必须先将方程化为一般形式二次项系数一次项系数常数项(a≠0) 在写一元二次方程的一般形式时,通常按未知数的次数从高到低排列,即先写二次项,再写一次项,最后是常数项。例1、把下列方程化成一元二次方程的一般形式,并写出它的二次项系数,一次项系数和常数项.1）移项，整理得9x2+4x-5=0
二次项系数是9，一次项系数是4，常数项是-5。3）移项，整理得4x2-5=0
二次项系数是4，一次项系数是0，常数项是-5。4）移项，整理得-3x2+2x+5=0
二次项系数是–3，一次项系数是2，常数项是5。注意：
1.要先化成 ax2+bx+c=0 的形式。
2.若方程中含有整式乘法，要先利用法则展开再进行等式变形。
3.在写一元二次方程一般式时，通常按未知数次数从高到低排列，即先写二次项，再写一次项，最后是常数项。写系数时，要带上前面的符号。 1、把下列方程化为一元二次方程的形式，并写出它的二次项系数、一次项系数和常数项：练一练x2-4x-3=0x2+x-8=07x2-4=01-4-3-8-41170（1）（2）（3）（4）答：a=1, b=3, c= -2.答：a=3, b=-5, c= 2.答：a=-2, b=-5, c= 3.答：a=6, b=1, c= -5.2、说出下列方程的二次项系数、一次项系数和常数项：练一练趁 热 打 铁 一元二次方程的解：能使一元二次方程两边相等的未知数的值叫一元二次方程的解或根。当x=0时，左边=02-2=-2，右边=0， 因为：左边≠右边解：当x=-1时，左边=（-1）2-2=1-2=-1 右边=-1 因为：左边=右边所以x=-1是方程的根。所以x=0不是方程的解。趁 热 打 铁3、判断未知数的值x=-1,x=o,x=2是不是方程x2-2=x的根代入法！判断未知数的值x=-1,x=o,x=2是不是方程x2-2=x的根4、已知关于x的一元二次方程x2+ax+a=0的一个根是3，求a的值。解：由题意得
把x=3代入方程x2+ax+a=0得，32+3a+a=09+4a=04a=-9练一练大显身手例2、已知一元二次方程2x2+bx+c=o的两个根为x1= ，
求这个方程.解：将x1= ，x=-3代入方程2x2+bx+c=o,得　解得，知识回顾:求一个方程经常可以通过确定方程中的未知数
来实现的，所用的待定系数是怎样得到？1.关于x的方程 (k－3)x2 ＋ 2x－1＝0,当 k _______时，是一元二次方程．2.关于x的方程 (k2－1)x2 ＋ 2 (k－1) x ＋ 2k＋ 2＝0, 当k 时，是一元二次方程;
当 k 　时，是一元一次方程．≠3≠±1＝－13.若关于x的方程（m+1)x |m|+1 -2x+3m=0是一元二次方程,求m的值。做一做1、判断下列各题括号内未知数的值是不是方程的根：（1）x2-3x+2=0 (x1=1 x2=2 x3=3)练一练2、构造一个一元二次方程，要求：
（1）常数项为零；（2）有一根为2。ax２＋bx＋c＝０(a, b，c为常数, a≠０)2、一元二次方程的一般形式 １、一元二次方程的定义 3、会用一元二次方程表示实际生活中的数量关系畅谈收获练习3：一个包装盒的表面展开图如图，包装盒的容积为750cm3.请写出关于x的方程.该方程是一元一次方程吗?如果是，把它化为一元一次方程的一般形式.单位：cm解：由题意得该方程是一元一次方程。它的一元一次方程的一般形式x2-15x+50=0
已知关于x的一元二次方程 ax2+bx+c=0 (a≠0)一个根为1, 求a+b+c的值. 解：由题意得思考:若 a+b+c=0,你能通过观察,求出方程ax2+bx+c=0 (a≠0)一个根吗? 解：由题意得∴方程ax2+bx+c=0 (a≠0)一个根是1.拓展:若 a-b +c=0, 你能通过观察,求出方程ax2+bx+c=0 (a≠0)一个根吗? 4a+2b +c=0拓展练习布置作业： 1.作业本(1分册2.1（p.5-6.) 2.课时特训A类做第1到14题； B类做第1到11题； C类做1到7题(p.16-17.) 再见