浙教版九下1.1 锐角三角函数(第二课时) 课件(共15张PPT)
文档属性
| 名称 | 浙教版九下1.1 锐角三角函数(第二课时) 课件(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
1.1 锐角三角函数
第二课时
浙教版九年级下册
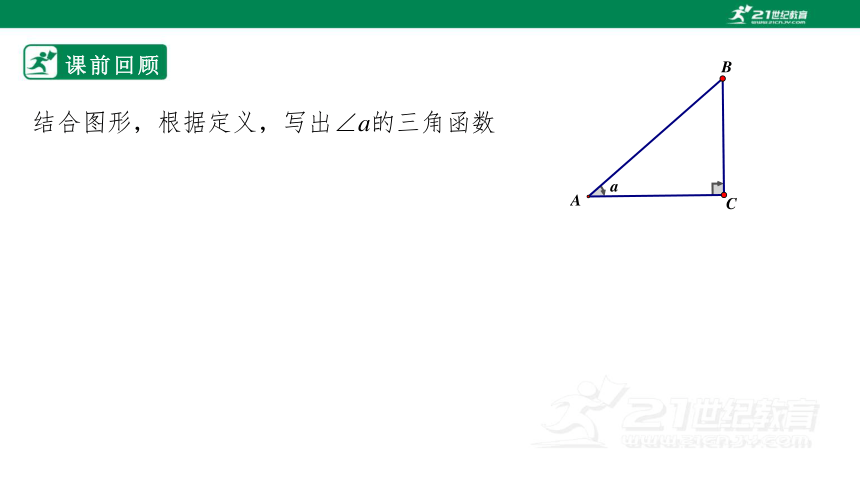
课前回顾
结合图形,根据定义,写出∠a的三角函数
导入新知
A
α
C
B
若α为30°,45°,60°,
则sinα,cosα,tanα的值分别是多少?
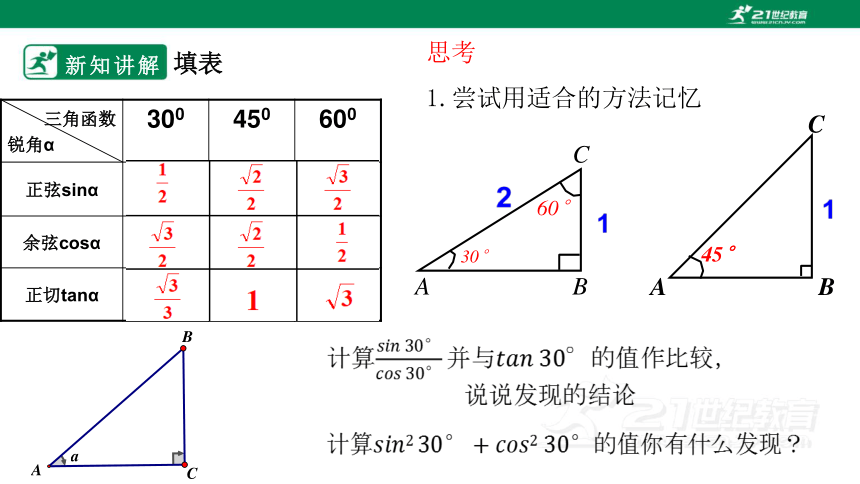
新知讲解
三角函数
锐角α 300
450
600
正弦sinα
余弦cosα
正切tanα
填表
思考
1.尝试用适合的方法记忆
60°
C
B
A
30°
A
B
C
45°
总结
1.同角公式
sin2A+cos2A=1
tanA=
2.当∠A+∠B=90°时,
sinA=cosB,
cosA=sinB,
tanA·tanB=1.
记录在第8页表格左侧
新知讲解
提示:
cos2450表示(cos450)2.
例:利用特殊的三角函数值进行计算:
(1)2sin 30°-3cos 60°
(2)sin245°+tan 60°. sin 60°
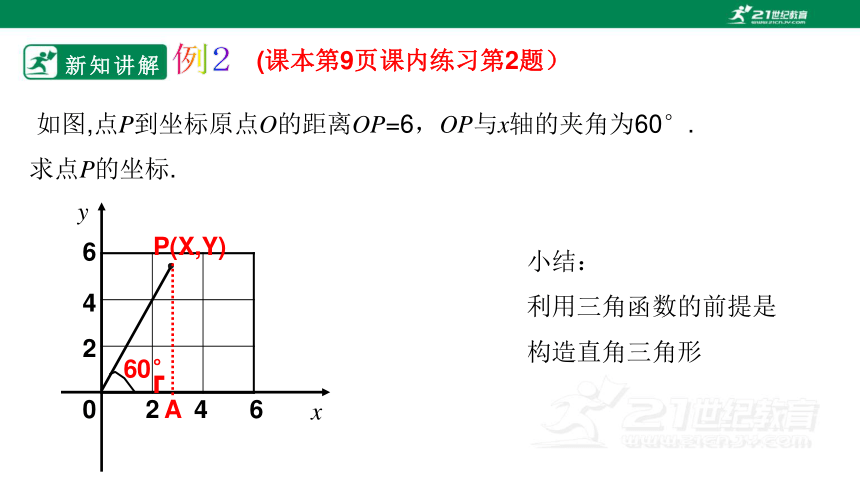
新知讲解
如图,点P到坐标原点O的距离OP=6,OP与x轴的夹角为60°.
求点P的坐标.
x
y
4
2
0 2 4 6
6
60°
P(X,Y)
┏
A
(课本第9页课内练习第2题)
小结:
利用三角函数的前提是构造直角三角形
巩固提升
已知点P的坐标如图,求点P的纵坐标和OP的长.
x
y
4
2
0 2 4 6
6
30°
P(6,y)
(课本第10页课内练习第3题)
拓展
如图,在△ABC中,AB=AC=6cm,∠BAC=120°.
求BC的长和△ABC的面积.
思考
如何构造直角三角形?
说说你的想法
巩固提升
1.如图,在Rt△ABC中,CD为斜边AB上的高,根据下列条件,回答问题:
(1)若BC=3,AC=4,求COS∠ ACD
(2)若BD=2,AD=8,求tan ∠A
B
C
D
A
2.在△ABC中,∠C=90゜,∠A,∠B,∠C的对边分别为a,b,c,下列式子中一定成立的是( )
A.a=c·cosB B.a= b· cosB C.a=c · tanB D.a=b · tanB
A
巩固提升
3.在△ABC中,若 ,
△ABC是( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
B
自我挑战
要求tan30°的值,可构造如图所示的直角三角形进行计算:
作Rt⊿ABC,使∠C =90°,斜边AB=2,直角边AC=1,则BC= ,∠ABC=30°,
∴tan30°= ,在此图的基础上,通过
添加适当的辅助线,可求出tan15°的值,请简要写出你添加的辅助线和求出的tan15°的值.
A
C
B
tan22.5°=
总结
1.同角公式
sin2A+cos2A=1
tanA=
2.当∠A+∠B=90°时,
sinA=cosB,
cosA=sinB,
tanA·tanB=1.
三角函数
锐角α 300
450
600
正弦sinα
余弦cosα
正切tanα
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
1.1 锐角三角函数
第二课时
浙教版九年级下册
课前回顾
结合图形,根据定义,写出∠a的三角函数
导入新知
A
α
C
B
若α为30°,45°,60°,
则sinα,cosα,tanα的值分别是多少?
新知讲解
三角函数
锐角α 300
450
600
正弦sinα
余弦cosα
正切tanα
填表
思考
1.尝试用适合的方法记忆
60°
C
B
A
30°
A
B
C
45°
总结
1.同角公式
sin2A+cos2A=1
tanA=
2.当∠A+∠B=90°时,
sinA=cosB,
cosA=sinB,
tanA·tanB=1.
记录在第8页表格左侧
新知讲解
提示:
cos2450表示(cos450)2.
例:利用特殊的三角函数值进行计算:
(1)2sin 30°-3cos 60°
(2)sin245°+tan 60°. sin 60°
新知讲解
如图,点P到坐标原点O的距离OP=6,OP与x轴的夹角为60°.
求点P的坐标.
x
y
4
2
0 2 4 6
6
60°
P(X,Y)
┏
A
(课本第9页课内练习第2题)
小结:
利用三角函数的前提是构造直角三角形
巩固提升
已知点P的坐标如图,求点P的纵坐标和OP的长.
x
y
4
2
0 2 4 6
6
30°
P(6,y)
(课本第10页课内练习第3题)
拓展
如图,在△ABC中,AB=AC=6cm,∠BAC=120°.
求BC的长和△ABC的面积.
思考
如何构造直角三角形?
说说你的想法
巩固提升
1.如图,在Rt△ABC中,CD为斜边AB上的高,根据下列条件,回答问题:
(1)若BC=3,AC=4,求COS∠ ACD
(2)若BD=2,AD=8,求tan ∠A
B
C
D
A
2.在△ABC中,∠C=90゜,∠A,∠B,∠C的对边分别为a,b,c,下列式子中一定成立的是( )
A.a=c·cosB B.a= b· cosB C.a=c · tanB D.a=b · tanB
A
巩固提升
3.在△ABC中,若 ,
△ABC是( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
B
自我挑战
要求tan30°的值,可构造如图所示的直角三角形进行计算:
作Rt⊿ABC,使∠C =90°,斜边AB=2,直角边AC=1,则BC= ,∠ABC=30°,
∴tan30°= ,在此图的基础上,通过
添加适当的辅助线,可求出tan15°的值,请简要写出你添加的辅助线和求出的tan15°的值.
A
C
B
tan22.5°=
总结
1.同角公式
sin2A+cos2A=1
tanA=
2.当∠A+∠B=90°时,
sinA=cosB,
cosA=sinB,
tanA·tanB=1.
三角函数
锐角α 300
450
600
正弦sinα
余弦cosα
正切tanα
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
