【新课标】2.1 直线和圆的位置关系(2) 课件(共28张PPT)
文档属性
| 名称 | 【新课标】2.1 直线和圆的位置关系(2) 课件(共28张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 00:00:00 | ||
图片预览





文档简介
(共28张PPT)
2.1 直线和圆的位置关系(2)
浙教版九年级下册
教学目标
1.理解直线与圆相切的判定定理;
2.会用切线的判定定理解决简单的问题;
3.通过判定定理的学习,培养观察、分析、归纳问题的能力,充分领会数学转化思想。
教学重难点
重点:
理解切线的判定定理,会运用切线的判定定理解决简单的数学问题。
难点:
利用切线的判定定理解决几何问题中辅助线的添加和方法。
新知导入
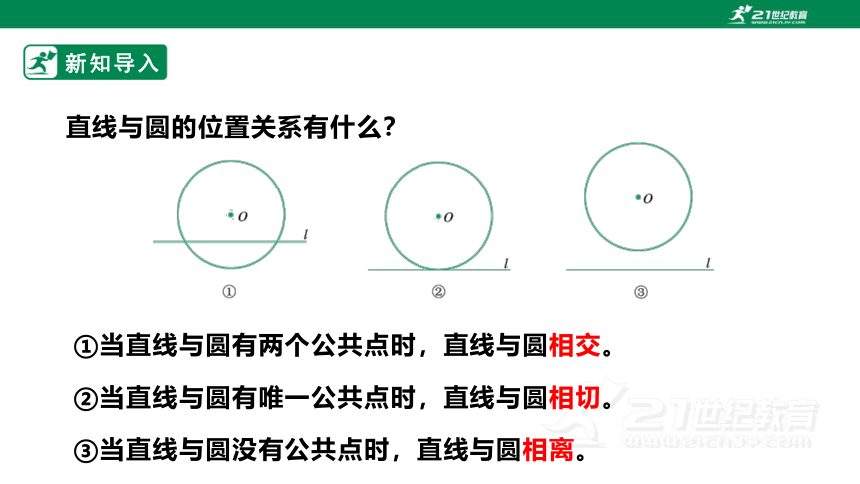
直线与圆的位置关系有什么?
①当直线与圆有两个公共点时,直线与圆相交。
②当直线与圆有唯一公共点时,直线与圆相切。
③当直线与圆没有公共点时,直线与圆相离。
新知导入
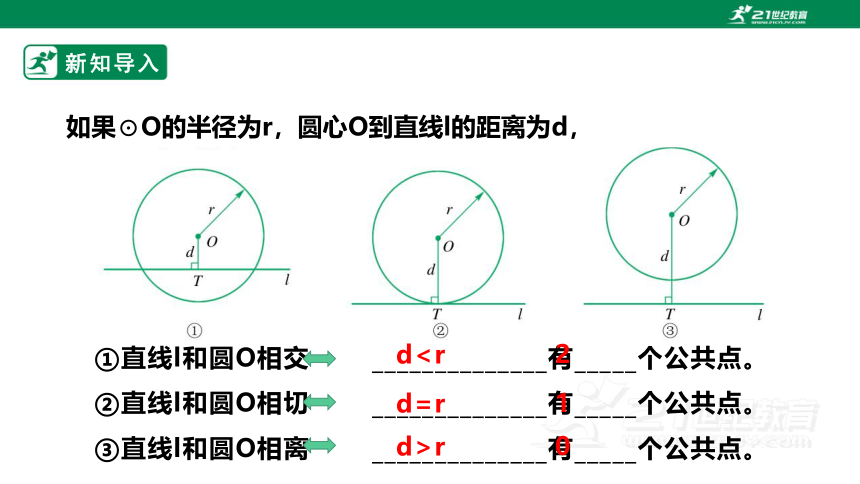
如果⊙O的半径为r,圆心O到直线l的距离为d,
①直线l和圆O相交 ______________有_____个公共点。
②直线l和圆O相切 ______________有_____个公共点。
③直线l和圆O相离 ______________有_____个公共点。
d2
d=r
1
d>r
0
新知讲解
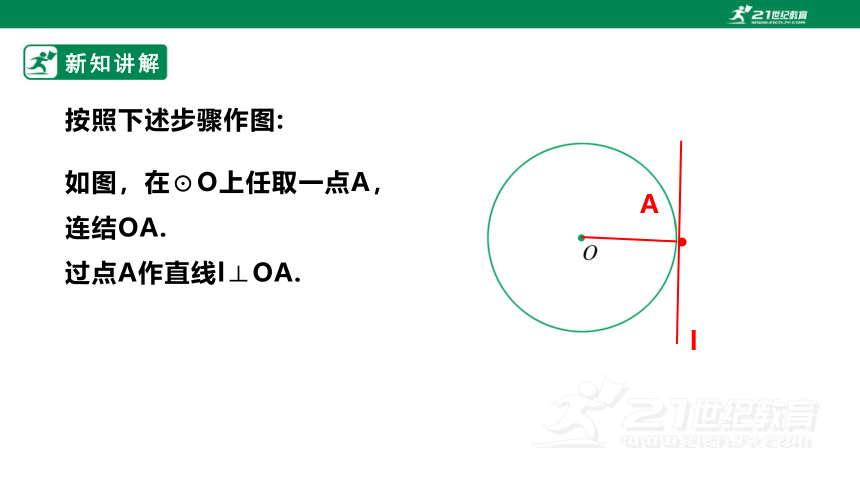
按照下述步骤作图:
如图,在⊙O上任取一点A,
连结OA.
过点A作直线l⊥OA.
A
·
l
新知讲解
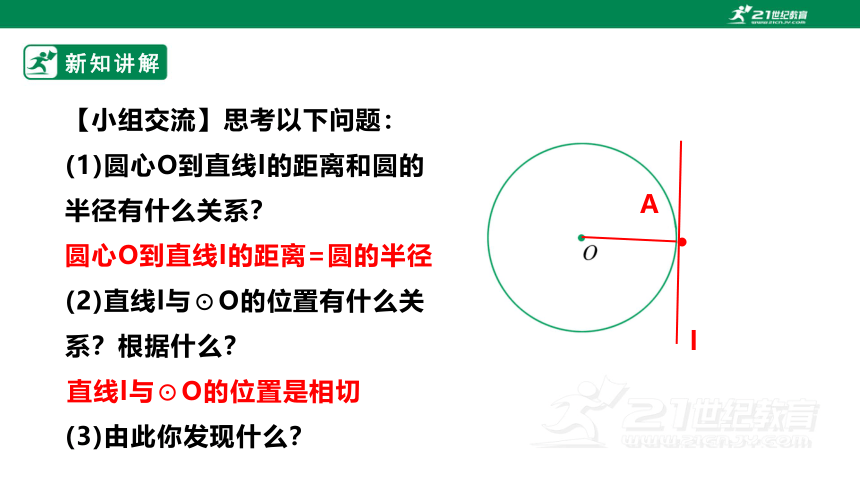
【小组交流】思考以下问题:
(1)圆心O到直线l的距离和圆的半径有什么关系?
(2)直线l与⊙O的位置有什么关系?根据什么?
(3)由此你发现什么?
A
·
l
圆心O到直线l的距离=圆的半径
直线l与⊙O的位置是相切
新知讲解
【总结归纳】
A
·
l
一般地,有以下直线与圆相切的判定定理:
经过半径的外端并且垂直这条半径的直线是圆的切线。
符号表示:
∵OA是半径,OA⊥l于A,
∴直线l是⊙O的切线。
新知讲解
【例】新知辨识
①过半径的外端的直线是圆的切线。( )
②与半径垂直的的直线是圆的切线。( )
③过半径的端点与半径垂直的直线是圆的切线。( )
×
×
×
新知讲解
【总结归纳】
用判定定理时,要注意直线需具备以下两个条件,缺一不可:
①直线经过半径的外端;
②直线与这条半径垂直。
新知讲解
【例3】已知:如图,A是⊙O外一点,AO的延长线交⊙O于点C,
点B在圆上,且AB=BC,∠A=30°. 求证:直线AB是⊙O的切线.
∵OB=OC,AB=BC, ∠A=30°, ∴∠OBC=∠C=∠A=30°,
∴∠AOB=∠C+∠OBC=60°,
证明:连结OB.
新知讲解
【例3】已知:如图,A是⊙O外一点,AO的延长线交⊙O于点C,
点B在圆上,且AB=BC,∠A=30°. 求证:直线AB是⊙O的切线.
∵∠ABO=180°-( ∠AOB+∠A )
=180°-( 60°+30° )=90°, ∴AB⊥OB,
∴ AB为⊙O的切线(经过半径的外端并且垂直这条半径的直线是圆的切线。)
新知讲解
【总结归纳】
判定一条直线是否为圆的切线主要有三种方法:
(1)利用定义;
(2)根据圆心到直线的距离等于圆的半径;
(3)经过半径外端并且垂直这条半径的直线是圆的切线.
新知讲解
【做一做】如图,AB是⊙O的直径 . 请分别过点A,B作⊙O的切线.
新知讲解
【例4】如图,台风中心P(100,200)沿北偏东30°方向移动,受台风影响区域的半径为200 km. 那么下列城市A(200,380), B(600,480),C(550,300),D(370,540)中,哪些受到这次台风的影响,哪些不受到这次台风的影响
新知讲解
解:如图,在直角坐标系中画出以点P(100,200)为圆心,以200为半径的⊙P,再在点P处画出北偏东30°方向的方向线,作垂直于方向线的⊙P的直径HK,分别过点H,K作⊙O的切线l1,l2,则l1//l2.
新知讲解
因为台风圈在两条平行线l1,l2之间移动,点A,D落在切线l1,l2之间,所以受到这次台风的影响;而点B,C不在切线l1,l2之间,所以不受到这次台风的影响.
新知讲解
证明圆的切线时常用的辅助线有哪些?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到半径,再证所作半径与这条直线垂直。简记为:有交点,连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段,再证垂线段长等于半径长。简记为:无交点作垂直,证半径。
【总结归纳】
课堂练习
1.如图,以点O为圆心作圆,所得的圆与直线a相切的是( )
A.以OA为半径的圆
B.以OB为半径的圆
C.以OC为半径的圆
D.以OD为半径的圆
D
课堂练习
2.如图,将直角三角板的直角顶点B放在⊙O上,直角边AB经过圆心O,则另一直角边BC与⊙O的位置关系为( )
A.相交
B.相切
C.相离
D.无法确定
B
课堂练习
3.如图,在平面直角坐标系中,过格点A,B,C画圆弧,则点B与下列格点连线所得的直线中,能够与该圆弧相切的格点坐标是( )
A.(5,3)
B.(2,4)
C.(1,4)
D.(6,2)
D
课堂练习
4.如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,下列说法不正确的是( )
A.若DE=DO,则DE是⊙O的切线
B.若AB=AC,则DE是⊙O的切线
C.若CD=DB,则DE是⊙O的切线
D.若DE是⊙O的切线,则AB=AC
A
课堂练习
5.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E.弦BF交CD于点G,点P在CD延长线上,且PF=PG. 求证:PF为⊙O的切线.
证明:如图,连结OF.
∵PF=PG,∴∠PFG=∠PGF.
∵OB=OF,∴∠OBF=∠OFB.
∵CD⊥AB,∴∠GEB=90°.
∴∠ABF+∠EGB=90°.
∵∠EGB=∠PGF,∴∠OFB+∠PFG=90°.
∴∠PFO=90°,即OF⊥PF.∴PF为⊙O的切线.
课堂总结
本节课你学到了什么?
判定圆的切线有哪些方法?
(1)定义:和圆有且只有一个公共点的直线是圆的切线。
(2)数量(d=r):和圆心距离等于半径的直线是圆的切线。
(3)定理:经过半径外端且垂直于这条半径的直线是圆的切线。
板书设计
课题:2.1 直线和圆的位置关系(2)
教师板演区
学生展示区
一、直线与圆相切的判定定理.
二、判断圆的切线的三种方法
三、画辅助线解决问题
作业布置
课本 P39 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.1 直线和圆的位置关系(2)
浙教版九年级下册
教学目标
1.理解直线与圆相切的判定定理;
2.会用切线的判定定理解决简单的问题;
3.通过判定定理的学习,培养观察、分析、归纳问题的能力,充分领会数学转化思想。
教学重难点
重点:
理解切线的判定定理,会运用切线的判定定理解决简单的数学问题。
难点:
利用切线的判定定理解决几何问题中辅助线的添加和方法。
新知导入
直线与圆的位置关系有什么?
①当直线与圆有两个公共点时,直线与圆相交。
②当直线与圆有唯一公共点时,直线与圆相切。
③当直线与圆没有公共点时,直线与圆相离。
新知导入
如果⊙O的半径为r,圆心O到直线l的距离为d,
①直线l和圆O相交 ______________有_____个公共点。
②直线l和圆O相切 ______________有_____个公共点。
③直线l和圆O相离 ______________有_____个公共点。
d
d=r
1
d>r
0
新知讲解
按照下述步骤作图:
如图,在⊙O上任取一点A,
连结OA.
过点A作直线l⊥OA.
A
·
l
新知讲解
【小组交流】思考以下问题:
(1)圆心O到直线l的距离和圆的半径有什么关系?
(2)直线l与⊙O的位置有什么关系?根据什么?
(3)由此你发现什么?
A
·
l
圆心O到直线l的距离=圆的半径
直线l与⊙O的位置是相切
新知讲解
【总结归纳】
A
·
l
一般地,有以下直线与圆相切的判定定理:
经过半径的外端并且垂直这条半径的直线是圆的切线。
符号表示:
∵OA是半径,OA⊥l于A,
∴直线l是⊙O的切线。
新知讲解
【例】新知辨识
①过半径的外端的直线是圆的切线。( )
②与半径垂直的的直线是圆的切线。( )
③过半径的端点与半径垂直的直线是圆的切线。( )
×
×
×
新知讲解
【总结归纳】
用判定定理时,要注意直线需具备以下两个条件,缺一不可:
①直线经过半径的外端;
②直线与这条半径垂直。
新知讲解
【例3】已知:如图,A是⊙O外一点,AO的延长线交⊙O于点C,
点B在圆上,且AB=BC,∠A=30°. 求证:直线AB是⊙O的切线.
∵OB=OC,AB=BC, ∠A=30°, ∴∠OBC=∠C=∠A=30°,
∴∠AOB=∠C+∠OBC=60°,
证明:连结OB.
新知讲解
【例3】已知:如图,A是⊙O外一点,AO的延长线交⊙O于点C,
点B在圆上,且AB=BC,∠A=30°. 求证:直线AB是⊙O的切线.
∵∠ABO=180°-( ∠AOB+∠A )
=180°-( 60°+30° )=90°, ∴AB⊥OB,
∴ AB为⊙O的切线(经过半径的外端并且垂直这条半径的直线是圆的切线。)
新知讲解
【总结归纳】
判定一条直线是否为圆的切线主要有三种方法:
(1)利用定义;
(2)根据圆心到直线的距离等于圆的半径;
(3)经过半径外端并且垂直这条半径的直线是圆的切线.
新知讲解
【做一做】如图,AB是⊙O的直径 . 请分别过点A,B作⊙O的切线.
新知讲解
【例4】如图,台风中心P(100,200)沿北偏东30°方向移动,受台风影响区域的半径为200 km. 那么下列城市A(200,380), B(600,480),C(550,300),D(370,540)中,哪些受到这次台风的影响,哪些不受到这次台风的影响
新知讲解
解:如图,在直角坐标系中画出以点P(100,200)为圆心,以200为半径的⊙P,再在点P处画出北偏东30°方向的方向线,作垂直于方向线的⊙P的直径HK,分别过点H,K作⊙O的切线l1,l2,则l1//l2.
新知讲解
因为台风圈在两条平行线l1,l2之间移动,点A,D落在切线l1,l2之间,所以受到这次台风的影响;而点B,C不在切线l1,l2之间,所以不受到这次台风的影响.
新知讲解
证明圆的切线时常用的辅助线有哪些?
(1)如果已知直线经过圆上一点,则连结这点和圆心,得到半径,再证所作半径与这条直线垂直。简记为:有交点,连半径,证垂直。
(2)如果已知条件中不知直线与圆是否有公共点,则过圆心作直线的垂线段,再证垂线段长等于半径长。简记为:无交点作垂直,证半径。
【总结归纳】
课堂练习
1.如图,以点O为圆心作圆,所得的圆与直线a相切的是( )
A.以OA为半径的圆
B.以OB为半径的圆
C.以OC为半径的圆
D.以OD为半径的圆
D
课堂练习
2.如图,将直角三角板的直角顶点B放在⊙O上,直角边AB经过圆心O,则另一直角边BC与⊙O的位置关系为( )
A.相交
B.相切
C.相离
D.无法确定
B
课堂练习
3.如图,在平面直角坐标系中,过格点A,B,C画圆弧,则点B与下列格点连线所得的直线中,能够与该圆弧相切的格点坐标是( )
A.(5,3)
B.(2,4)
C.(1,4)
D.(6,2)
D
课堂练习
4.如图,AB是⊙O的直径,BC交⊙O于点D,DE⊥AC于点E,下列说法不正确的是( )
A.若DE=DO,则DE是⊙O的切线
B.若AB=AC,则DE是⊙O的切线
C.若CD=DB,则DE是⊙O的切线
D.若DE是⊙O的切线,则AB=AC
A
课堂练习
5.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E.弦BF交CD于点G,点P在CD延长线上,且PF=PG. 求证:PF为⊙O的切线.
证明:如图,连结OF.
∵PF=PG,∴∠PFG=∠PGF.
∵OB=OF,∴∠OBF=∠OFB.
∵CD⊥AB,∴∠GEB=90°.
∴∠ABF+∠EGB=90°.
∵∠EGB=∠PGF,∴∠OFB+∠PFG=90°.
∴∠PFO=90°,即OF⊥PF.∴PF为⊙O的切线.
课堂总结
本节课你学到了什么?
判定圆的切线有哪些方法?
(1)定义:和圆有且只有一个公共点的直线是圆的切线。
(2)数量(d=r):和圆心距离等于半径的直线是圆的切线。
(3)定理:经过半径外端且垂直于这条半径的直线是圆的切线。
板书设计
课题:2.1 直线和圆的位置关系(2)
教师板演区
学生展示区
一、直线与圆相切的判定定理.
二、判断圆的切线的三种方法
三、画辅助线解决问题
作业布置
课本 P39 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
