【新课标】2.1 直线和圆的位置关系(3) 课件(共28张PPT)
文档属性
| 名称 | 【新课标】2.1 直线和圆的位置关系(3) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-01 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
2.1 直线和圆的位置关系(3)
浙教版九年级下册
教学目标
1.掌握切线的性质定理,并能运用圆的切线的性质解决相关的计算和证明。
2.能从逆向思维的角度理解切线的性质定理。
3.经历探究切线的性质定理的过程,掌握切线的基础知识和基本技能,并能解决简单的问题。
教学重难点
重点:
探索圆的切线的性质,并能运用它解决与圆的切线相关的计算和证明等问题。
难点:
综合运用圆的切线的判定和性质解决相关问题。
新知导入
1.如果直线AB和⊙O只有一个公共点,那么直线AB与⊙O的位置关系是_________.
2.已知⊙O的直径为8cm,圆心O到直线l的距离为4cm,则直线l与⊙O的位置关系是_________.
3.如图,作⊙O的半径OA,过点A作l⊥OA,垂足为A,那么直线l与⊙O有怎样的位置关系?
相切
相切
A
l
直线l与⊙O相切
新知导入
【思考】判定一条直线是否为圆的切线有几种方法?
(1)利用定义;
(2)根据圆心到直线的距离等于圆的半径;
(3)经过半径外端并且垂直这条半径的直线是圆的切线.
新知讲解
【小组合作】如图,直线AT与⊙O相切于点A,连结OA,P是AT上一点. ∠OAP等于多少度? 在⊙O上再任意取一些点,过各点作⊙O的切线,连结圆心与切点. 半径与切线所成的角为多少度?由此你发现了什么?
新知讲解
【总结归纳】
一般地,圆的切线有如下的性质:
经过切点的半径垂直于圆的切线。
符号语言:
∵AP是⊙O的切线,A为切点,
∴OA⊥AP.
新知讲解
【思考】切线的判定定理与性质定理有什么不同呢?
①过半径的外端
②垂直于这条半径
①圆的切线
②过切点的半径
圆的切线
切线的判定定理:
切线的性质定理:
切线垂直于半径
新知讲解
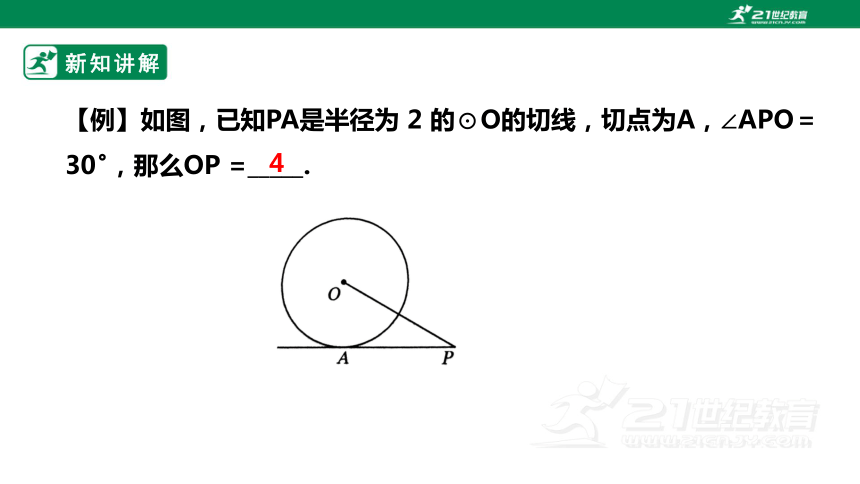
【例】如图,已知PA是半径为 2 的⊙O的切线,切点为A,∠APO=30 ,那么OP =_____.
4
新知讲解
【总结归纳】
①过圆心
②垂直于切线
③过切点
切线性质
知二推一
对于切线的性质定理的掌握可归纳为三条:
(1)过圆心;(2)过切点;(3)垂直于切线.
事实上只要知道其中两个性质,就可以推出第三个.
新知讲解
【例5】木工师傅可以用角尺测量并计算出圆的半径。如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O相切于点C. 记角尺的直角顶点为B,量得AB=8cm,BC=16cm. 求⊙O的半径.
分析:要求⊙O的半径,可以考虑建立与圆的半径有关的直角三角形,因为BC是⊙O的切线,所以连结OC,这样四边形ABCO是直角梯形,过A点作OC的垂线,求得圆的半径.
新知讲解
【例5】木工师傅可以用角尺测量并计算出圆的半径。如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O相切于点C. 记角尺的直角顶点为B,量得AB=8cm,BC=16cm. 求⊙O的半径.
解:连结OA,OC,作AD⊥OC,垂足为D.设⊙O的半径为r.
∵⊙O与BC相切于点C,
∴OC⊥BC(经过切点的半径垂直于圆的切线).
新知讲解
【例5】木工师傅可以用角尺测量并计算出圆的半径。如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O相切于点C. 记角尺的直角顶点为B,量得AB=8cm,BC=16cm. 求⊙O的半径.
∵AB⊥BC,AD⊥OC,
∴四边形 ABCD 是矩形,
∴AD=BC,DC=AB,
OD=OC-CD=OC-AB.
新知讲解
【例5】木工师傅可以用角尺测量并计算出圆的半径。如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O相切于点C. 记角尺的直角顶点为B,量得AB=8cm,BC=16cm. 求⊙O的半径.
在Rt△AOD中,OA2=AD2+OD2,
即r2=(r-8)2+162,
解得r=20.
∴⊙O的半径为20cm.
新知讲解
【例6】已知:如图,直线AB与⊙O相切于点C, AO交⊙O于点D,连结CD. 求证: ∠ACD= ∠COD.
分析:要证明∠ACD= ∠COD,需要找到一个角等于∠COD的一半,或者是∠ACD的两倍.因为直线AB与⊙O相切于点C,所以OC⊥AB,因此考虑作∠COD的平分线。
新知讲解
【例6】已知:如图,直线AB与⊙O相切于点C, AO交⊙O于点D,连结CD. 求证: ∠ACD= ∠COD.
证明:如图,作OE⊥CD于点E.
∵△ODC是等腰三角形,
∴∠COE= ∠COD,OE⊥CD,
即∠COE+∠OCE=Rt∠.
新知讲解
【例6】已知:如图,直线AB与⊙O相切于点C, AO交⊙O于点D,连结CD. 求证: ∠ACD= ∠COD.
∵⊙O与AB相切于点C,
∴OC⊥AB(经过切点的半径垂直于圆的切线).
即∠ACD+∠OCE=Rt∠.
∴∠ACD=COE,即∠ACD= ∠COD.
课堂练习
A
1.下列说法中,正确的是( ).
A.圆的切线垂直于经过切点的半径
B.垂直于切线的直线必经过切点
C.垂直于切线的直线必经过圆心
D.垂直于半径的直线是圆的切线
课堂练习
C
2.如图,AB是⊙O的直径,BC是⊙O的切线.若∠BAC=35°,则∠ACB的大小为( ).
A.35°
B.45°
C.55°
D.65°
课堂练习
3.如图,⊙O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是( ).
A.144°
B.130°
C.129°
D.108°
A
课堂练习
4.一根钢管放在V形架内,其横截面如图所示,钢管的半径是24 cm.若∠ACB=60°,则劣弧AB的长是( ).
A.8π cm
B.16π cm
C.32π cm
D.192π cm
B
课堂练习
5.如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D. 求证:AC平分∠DAB.
证明:连结OC.
∵CD是⊙O的切线,∴∠OCD=90°.
∵AD⊥CD,∴∠ADC=∠OCD=90°.
∴∠ADC+∠OCD=180°.
∴AD∥OC. ∴∠DAC=∠ACO.
∵OA=OC,∴∠ACO=∠OAC.
∴∠DAC=∠OAC. ∴AC平分∠DAB.
课堂练习
6.如图,AB为⊙O的直径,C为BA延长线上一点,CD是⊙O的切线,D为切点,OF⊥AD于点E,交CD于点F. 求证:∠ADC=∠AOF.
证明:连结OD.
∵CD是⊙O的切线,∴CD⊥OD.
∴∠CDO=∠ADC+∠ADO=90°.
∵OA=OD,∴∠ADO=∠DAO.
∵ OF⊥AD于点E, ∴∠DAO+∠AOF=90°.
∴∠ADC=∠AOF.
课堂总结
本节课你学到了什么?
圆的切线的性质:
经过切点的半径垂直于圆的切线。
符号语言:
∵AP是⊙的切线,A为切点,
∴OA⊥AP.
板书设计
课题:2.1 直线和圆的位置关系(3)
教师板演区
学生展示区
一、圆的切线的性质
二、圆的切线的判定定理与性质定理的区别
三、解决问题
作业布置
课本 P42 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.1 直线和圆的位置关系(3)
浙教版九年级下册
教学目标
1.掌握切线的性质定理,并能运用圆的切线的性质解决相关的计算和证明。
2.能从逆向思维的角度理解切线的性质定理。
3.经历探究切线的性质定理的过程,掌握切线的基础知识和基本技能,并能解决简单的问题。
教学重难点
重点:
探索圆的切线的性质,并能运用它解决与圆的切线相关的计算和证明等问题。
难点:
综合运用圆的切线的判定和性质解决相关问题。
新知导入
1.如果直线AB和⊙O只有一个公共点,那么直线AB与⊙O的位置关系是_________.
2.已知⊙O的直径为8cm,圆心O到直线l的距离为4cm,则直线l与⊙O的位置关系是_________.
3.如图,作⊙O的半径OA,过点A作l⊥OA,垂足为A,那么直线l与⊙O有怎样的位置关系?
相切
相切
A
l
直线l与⊙O相切
新知导入
【思考】判定一条直线是否为圆的切线有几种方法?
(1)利用定义;
(2)根据圆心到直线的距离等于圆的半径;
(3)经过半径外端并且垂直这条半径的直线是圆的切线.
新知讲解
【小组合作】如图,直线AT与⊙O相切于点A,连结OA,P是AT上一点. ∠OAP等于多少度? 在⊙O上再任意取一些点,过各点作⊙O的切线,连结圆心与切点. 半径与切线所成的角为多少度?由此你发现了什么?
新知讲解
【总结归纳】
一般地,圆的切线有如下的性质:
经过切点的半径垂直于圆的切线。
符号语言:
∵AP是⊙O的切线,A为切点,
∴OA⊥AP.
新知讲解
【思考】切线的判定定理与性质定理有什么不同呢?
①过半径的外端
②垂直于这条半径
①圆的切线
②过切点的半径
圆的切线
切线的判定定理:
切线的性质定理:
切线垂直于半径
新知讲解
【例】如图,已知PA是半径为 2 的⊙O的切线,切点为A,∠APO=30 ,那么OP =_____.
4
新知讲解
【总结归纳】
①过圆心
②垂直于切线
③过切点
切线性质
知二推一
对于切线的性质定理的掌握可归纳为三条:
(1)过圆心;(2)过切点;(3)垂直于切线.
事实上只要知道其中两个性质,就可以推出第三个.
新知讲解
【例5】木工师傅可以用角尺测量并计算出圆的半径。如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O相切于点C. 记角尺的直角顶点为B,量得AB=8cm,BC=16cm. 求⊙O的半径.
分析:要求⊙O的半径,可以考虑建立与圆的半径有关的直角三角形,因为BC是⊙O的切线,所以连结OC,这样四边形ABCO是直角梯形,过A点作OC的垂线,求得圆的半径.
新知讲解
【例5】木工师傅可以用角尺测量并计算出圆的半径。如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O相切于点C. 记角尺的直角顶点为B,量得AB=8cm,BC=16cm. 求⊙O的半径.
解:连结OA,OC,作AD⊥OC,垂足为D.设⊙O的半径为r.
∵⊙O与BC相切于点C,
∴OC⊥BC(经过切点的半径垂直于圆的切线).
新知讲解
【例5】木工师傅可以用角尺测量并计算出圆的半径。如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O相切于点C. 记角尺的直角顶点为B,量得AB=8cm,BC=16cm. 求⊙O的半径.
∵AB⊥BC,AD⊥OC,
∴四边形 ABCD 是矩形,
∴AD=BC,DC=AB,
OD=OC-CD=OC-AB.
新知讲解
【例5】木工师傅可以用角尺测量并计算出圆的半径。如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O相切于点C. 记角尺的直角顶点为B,量得AB=8cm,BC=16cm. 求⊙O的半径.
在Rt△AOD中,OA2=AD2+OD2,
即r2=(r-8)2+162,
解得r=20.
∴⊙O的半径为20cm.
新知讲解
【例6】已知:如图,直线AB与⊙O相切于点C, AO交⊙O于点D,连结CD. 求证: ∠ACD= ∠COD.
分析:要证明∠ACD= ∠COD,需要找到一个角等于∠COD的一半,或者是∠ACD的两倍.因为直线AB与⊙O相切于点C,所以OC⊥AB,因此考虑作∠COD的平分线。
新知讲解
【例6】已知:如图,直线AB与⊙O相切于点C, AO交⊙O于点D,连结CD. 求证: ∠ACD= ∠COD.
证明:如图,作OE⊥CD于点E.
∵△ODC是等腰三角形,
∴∠COE= ∠COD,OE⊥CD,
即∠COE+∠OCE=Rt∠.
新知讲解
【例6】已知:如图,直线AB与⊙O相切于点C, AO交⊙O于点D,连结CD. 求证: ∠ACD= ∠COD.
∵⊙O与AB相切于点C,
∴OC⊥AB(经过切点的半径垂直于圆的切线).
即∠ACD+∠OCE=Rt∠.
∴∠ACD=COE,即∠ACD= ∠COD.
课堂练习
A
1.下列说法中,正确的是( ).
A.圆的切线垂直于经过切点的半径
B.垂直于切线的直线必经过切点
C.垂直于切线的直线必经过圆心
D.垂直于半径的直线是圆的切线
课堂练习
C
2.如图,AB是⊙O的直径,BC是⊙O的切线.若∠BAC=35°,则∠ACB的大小为( ).
A.35°
B.45°
C.55°
D.65°
课堂练习
3.如图,⊙O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是( ).
A.144°
B.130°
C.129°
D.108°
A
课堂练习
4.一根钢管放在V形架内,其横截面如图所示,钢管的半径是24 cm.若∠ACB=60°,则劣弧AB的长是( ).
A.8π cm
B.16π cm
C.32π cm
D.192π cm
B
课堂练习
5.如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D. 求证:AC平分∠DAB.
证明:连结OC.
∵CD是⊙O的切线,∴∠OCD=90°.
∵AD⊥CD,∴∠ADC=∠OCD=90°.
∴∠ADC+∠OCD=180°.
∴AD∥OC. ∴∠DAC=∠ACO.
∵OA=OC,∴∠ACO=∠OAC.
∴∠DAC=∠OAC. ∴AC平分∠DAB.
课堂练习
6.如图,AB为⊙O的直径,C为BA延长线上一点,CD是⊙O的切线,D为切点,OF⊥AD于点E,交CD于点F. 求证:∠ADC=∠AOF.
证明:连结OD.
∵CD是⊙O的切线,∴CD⊥OD.
∴∠CDO=∠ADC+∠ADO=90°.
∵OA=OD,∴∠ADO=∠DAO.
∵ OF⊥AD于点E, ∴∠DAO+∠AOF=90°.
∴∠ADC=∠AOF.
课堂总结
本节课你学到了什么?
圆的切线的性质:
经过切点的半径垂直于圆的切线。
符号语言:
∵AP是⊙的切线,A为切点,
∴OA⊥AP.
板书设计
课题:2.1 直线和圆的位置关系(3)
教师板演区
学生展示区
一、圆的切线的性质
二、圆的切线的判定定理与性质定理的区别
三、解决问题
作业布置
课本 P42 练习题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
