2.2一元二次方程的解法（3）

课件18张PPT。泰顺六中 翁怀新2014年3月10日2.2一元二次方程的解法（3）1、一元二次方程的一般形式：常数项二次项， 二次项系数一次项， 一次项系数 复习回顾（2）直接开平方法（3）配方法（1）因式分解法2、一元二次方程的解法：（4）十字相乘法复习回顾3、用配方法解下列一元二次方程：（1）x2-8x=4 (2) -x2+5x+6=0解:(1)方程两边都加上16，得x2- 8x+16=4+16,即（ x-4)2=20 解：（2）化简，得 x2-5x=6，方程两边同时加上25/4，得x2-5x+25/4=6+25/4 即（ x- 5/2 )2=49/4， 则x-5/2=7/2，或x-5/2=-7/2，解得x1=6,x2=-14、配方法解一元二次方程的基本步骤:(1)移项:把常数项移到方程的右边;
(2)配方:方程两边都加上一次项系数一半的平方;
(3)开方:根据平方根意义,方程两边开平方;
(4)求解:解两个一元一次方程;
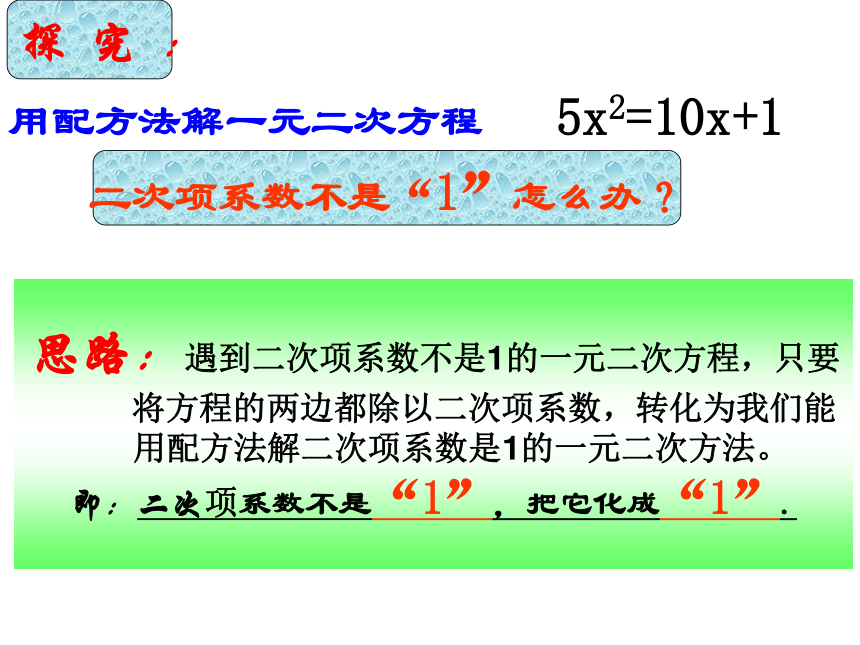
(5)定解:写出原方程的解.复习回顾即★一移、二配、三化、四解、五定.用配方法解一元二次方程 5x2=10x+1探究：二次项系数不是“1”怎么办？思路：遇到二次项系数不是1的一元二次方程，只要
将方程的两边都除以二次项系数，转化为我们能
用配方法解二次项系数是1的一元二次方法。
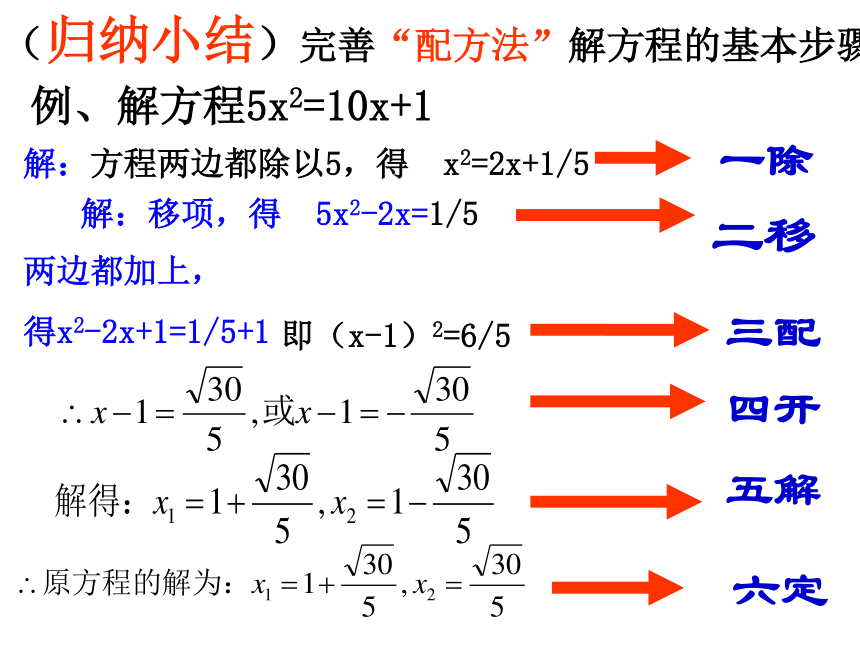
即：二次项系数不是“1”，把它化成“1”.例、解方程5x2=10x+1解：移项，得 5x2-2x=1/5解：方程两边都除以5，得 x2=2x+1/5两边都加上，
得x2-2x+1=1/5+1即（x-1）2=6/5（归纳小结）完善“配方法”解方程的基本步骤：一除二移三配四开五解六定
★一除、二移、三配、四开、五解、六定.完善“配方法”解方程的基本步骤：(1)除a：把二次项系数化为“1”(方程的两边同时除以二次项系数a)
(2)移项:把常数项移到方程的右边;
(3)配方:方程两边都加上一次项系数一半的平方;
(4)开方:根据平方根意义,方程两边开平方;
(5)求解:解两个一元一次方程;
(6)定解:写出原方程的解.
练一练用配方法解 时,配方结果正确的是( )解：方程两边同除以2，得解：方程两边同除以2，得x2-8/3x-1=0x2+2x-3/2=0移项，得 x2+2x=3/2移项，得 x2-8/3x=1方程两边都加上1，得方程两边都加上16/9，得x2+2x+1=5/2x2-8/3x+16/9=25/9即：(x+1)2=5/2即：（x-4/3)2=25/9∴x- 4/3= 5/3
或x- 4/3=- 5/3 ∴x1=3 或x2=-1/3 ∴x+1= 或x+1=- ∴x1=-1+ 或x2=-1- 例6、用配方法解下列一元二次方程(1) 2x2+4x-3=0 (2) 3x2-8x-3=0练一练解：原式=2（x2-2x）+7=2（x2-2x+1）-2+7=2(x-1)2+5例7、已知4x2+8(n+1)x+16n是一个关于x的完全平方式.求常数n的值例7、已知4x2+8(n+1)x+16n是一个关于x的
完全平方式,求常数n的值.解：原式=4[x2+2(n+1)x]+16n =4[x2+2(n+1)x+(n+1)2]-4(n+1)2+16n =4(x+n+1)2-4(n+1)2+16n化简，得n2-2n+1=0, 即 (n-1)2=0解得n1=n2=1所以常数n的值为1.已知4x2+8(n+1)x+16n是一个完全平方式,
则 -4(n+1)2+16n=0分析：当n为常数时，已知代数式就是关于x的二次三项式，它的二项系数为4，一次项系数为8(n+1),常数项为16n,要使这个二次三项式为一个完全平方式，那么这个完全平方式应具有4(a±b)2的形式。区别:
1.概念不一样.
2.代数式不用等号连接.
3.方程是含有未知数的等式.其未知数(变量)的
个数不固定.未知数之间不存在自变和因变的关系.代数式:用运算符号把数或表示数的字母连接而成
的式子,叫代数式. 方程:含有未知数的等式叫方程.
代数式的配方与方程的配方有何区别？拓展练习：用配方法说明：不论x取任何实数，多项式2x2-4x+7 的值必大于零. 解：2x2+4x+7
=2(x2-2x)+7
=2(x2-2x+1)-2+7
=2(x-1)2+5 因为不论x取任何实数,(x-1)2≥0，
即2(x+1)2+5的值大于或等于5，因此不论x取任何实数，多项式2x2-4x+7 的值必大于零.练一练1.用配方法解下列方程:
2x2+6x+3=0
2x2-7x+5=0练一练2.用配方法解下列方程:
0.2x2+0.4x=1
x2 - x - =0
- 3n=01、一个知识点：用配方法解二次项系数不是“1”的一元二次方程基本步骤：
★一除、二移、三配、四开、五解、六定.思路：遇到二次项系数不是1的一元二次方程，只要
将方程的两边都除以二次项系数，转化为我们能
用配方法解二次项系数是1的一元二次方法。
即：二次项系数不是“1”，把它化成“1”.配方法解二次项系数是1的一元二次方程的基本步骤：
即★一移、二配、三化、四解、五定.2、一个方法：如果二次项系数是1时，常数项配一次项系数一半的平方.3、一个思想：化归的思想，即当二次项系数不是1时，把它化为1. 布置作业：
1.作业本(1分册2.2(3)（p.9-10.)
2.课时特训A类做第1到12题；
B类做第1到16题和第8题；
C类做1到6题(p.22-24.) 再见