2.3一元二次方程的应用(2)
图片预览






文档简介
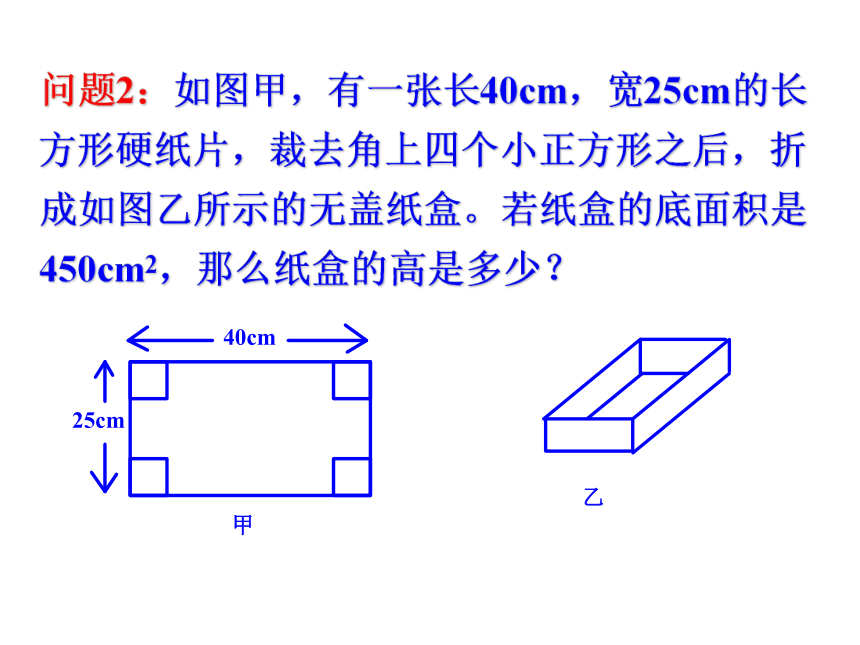
课件14张PPT。2.3一元二次方程的应用(2)面积问题如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米?解:设道路宽为x米,则化简得,其中的 x=35超出了原矩形的宽,应舍去.答:道路的宽为1米.问题1:问题2:如图甲,有一张长40cm,宽25cm的长方形硬纸片,裁去角上四个小正方形之后,折成如图乙所示的无盖纸盒。若纸盒的底面积是450cm2,那么纸盒的高是多少? 练习1
1、取一张长与宽之比5:2的长方形纸板,剪去四个边长为5cm的小正方形,并用它做一个无盖的长方体形状的包装盒。要使包装盒的容积为200cm3,这张长方形纸板的长与宽分别是多少厘米?在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是【 】
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0B 练习2
行程问题(线段长度问题)B1C1 一轮船以30km/h的速度由西向东航行,在途中接到台风警报,台风中心正以20km/h的速度由南向北移动。已知距台风中心200km的区域(包括边界)都属于受台风影响区,当轮船接到台风警报时,测得BC=500km,BA=300km.
(1)如果轮船不改变航向,轮船会不会进入台风影响区?你采用什么方法来判断?
(2)如果你认为轮船会进入台风影响区,那么从接到警报开始,经多少时间进入台风影响区?500km300km200km问题1 :解:设当轮船接到台风警报后,经过t小时,
则:令
(400-30t)2+(300-20t)2=2002问:(1) 这方程解得的t1,t2的实际意义是什么?(2) 从t1,t2的值中,还可得到什么结论?t1 8.35 t2 19.34(3) 如何才能避免轮船不进入台风影响区?提高题:(4) 这艘轮船受台风影响的时间有多长?问题2:1、如图,在△ABC中,∠B=90o。点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动。如果P、Q分别
从A,B同时出发,经过
几秒, △ PBQ的面积
等于8cm2 ?如图,矩形ABCD中,AB=6cm,BC=3cm,动点P、Q分别从点A、D出发,点P以2cm/s的速度沿AB方向向点B移动,一直到达B为止;点Q以1cm/s的速度沿DA方向向点A移动。如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤3)那么,当为何值时△QAP的面积等于2cm2?练习1:1.如图,是长方形鸡场平面示意图,一边靠墙,墙长18米另外三面用竹篱笆围成,若竹篱笆总长为35米,所围的面积为150m2,则此长方形鸡场的长、宽分别为_______.提高题1:如图,有长为12米的篱笆,一面利用墙(墙的最大可用长度为a为10米),围成中间隔有一道篱笆的长方形花圃。
(1)如果要围成面积为9平方米的花圃,AB的长是多少米?
(2)能围成面积比9平方米更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由。提高题2:这里要特别注意:在列一元二次方程解应用题时,由于所得的根一般有两个,所以要检验这两个根是否符合实际问题的要求. 列一元二次方程解应用题的步骤与
列一元一次方程解应用题的步骤类似,
即审、设、列、解、检、答.小结
1、取一张长与宽之比5:2的长方形纸板,剪去四个边长为5cm的小正方形,并用它做一个无盖的长方体形状的包装盒。要使包装盒的容积为200cm3,这张长方形纸板的长与宽分别是多少厘米?在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是【 】
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0B 练习2
行程问题(线段长度问题)B1C1 一轮船以30km/h的速度由西向东航行,在途中接到台风警报,台风中心正以20km/h的速度由南向北移动。已知距台风中心200km的区域(包括边界)都属于受台风影响区,当轮船接到台风警报时,测得BC=500km,BA=300km.
(1)如果轮船不改变航向,轮船会不会进入台风影响区?你采用什么方法来判断?
(2)如果你认为轮船会进入台风影响区,那么从接到警报开始,经多少时间进入台风影响区?500km300km200km问题1 :解:设当轮船接到台风警报后,经过t小时,
则:令
(400-30t)2+(300-20t)2=2002问:(1) 这方程解得的t1,t2的实际意义是什么?(2) 从t1,t2的值中,还可得到什么结论?t1 8.35 t2 19.34(3) 如何才能避免轮船不进入台风影响区?提高题:(4) 这艘轮船受台风影响的时间有多长?问题2:1、如图,在△ABC中,∠B=90o。点P从点A开始沿边AB向点B以1cm/s的速度移动,与此同时,点Q从点B开始沿边BC向点C以2cm/s的速度移动。如果P、Q分别
从A,B同时出发,经过
几秒, △ PBQ的面积
等于8cm2 ?如图,矩形ABCD中,AB=6cm,BC=3cm,动点P、Q分别从点A、D出发,点P以2cm/s的速度沿AB方向向点B移动,一直到达B为止;点Q以1cm/s的速度沿DA方向向点A移动。如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤3)那么,当为何值时△QAP的面积等于2cm2?练习1:1.如图,是长方形鸡场平面示意图,一边靠墙,墙长18米另外三面用竹篱笆围成,若竹篱笆总长为35米,所围的面积为150m2,则此长方形鸡场的长、宽分别为_______.提高题1:如图,有长为12米的篱笆,一面利用墙(墙的最大可用长度为a为10米),围成中间隔有一道篱笆的长方形花圃。
(1)如果要围成面积为9平方米的花圃,AB的长是多少米?
(2)能围成面积比9平方米更大的花圃吗?如果能,请求出最大面积,并说明围法;如果不能,请说明理由。提高题2:这里要特别注意:在列一元二次方程解应用题时,由于所得的根一般有两个,所以要检验这两个根是否符合实际问题的要求. 列一元二次方程解应用题的步骤与
列一元一次方程解应用题的步骤类似,
即审、设、列、解、检、答.小结
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
