2.3 一元二次方程的应用

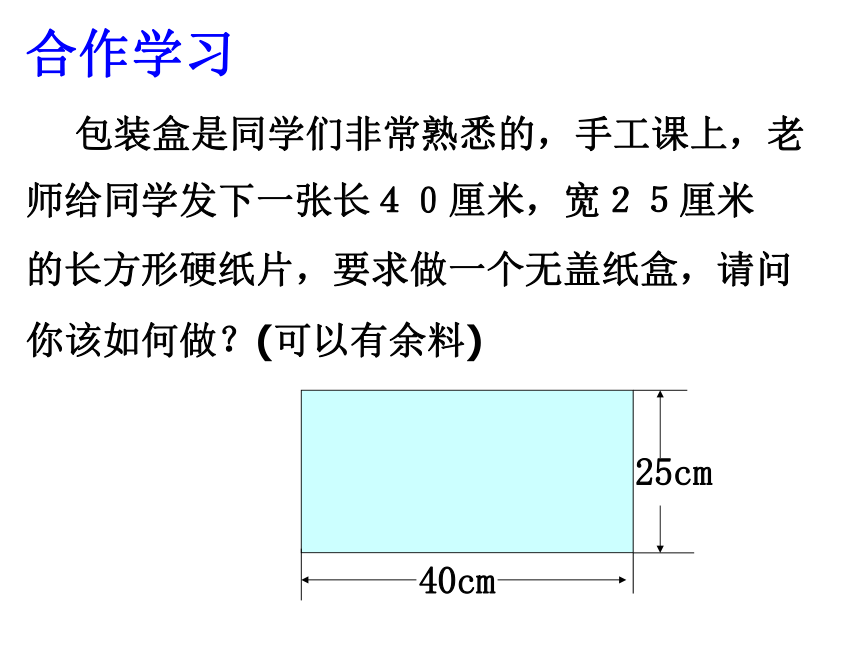
课件23张PPT。课题2.3 一元二次方程的应用（2）赤溪中心学校　 包装盒是同学们非常熟悉的，手工课上，老师给同学发下一张长４０厘米，宽２５厘米
的长方形硬纸片，要求做一个无盖纸盒，请问你该如何做？(可以有余料)合作学习请问：
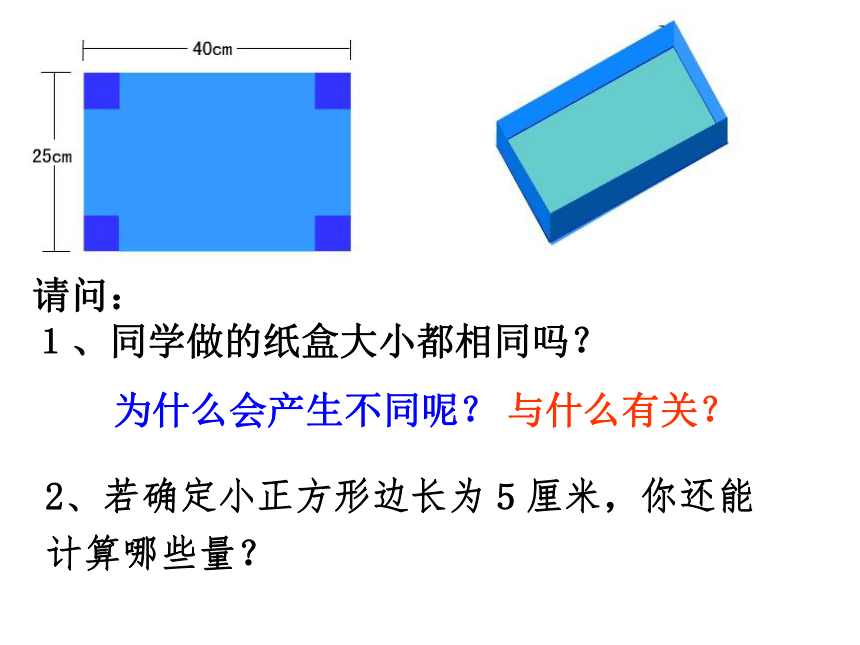
１、同学做的纸盒大小都相同吗？与什么有关？为什么会产生不同呢？2、若确定小正方形边长为５厘米，你还能
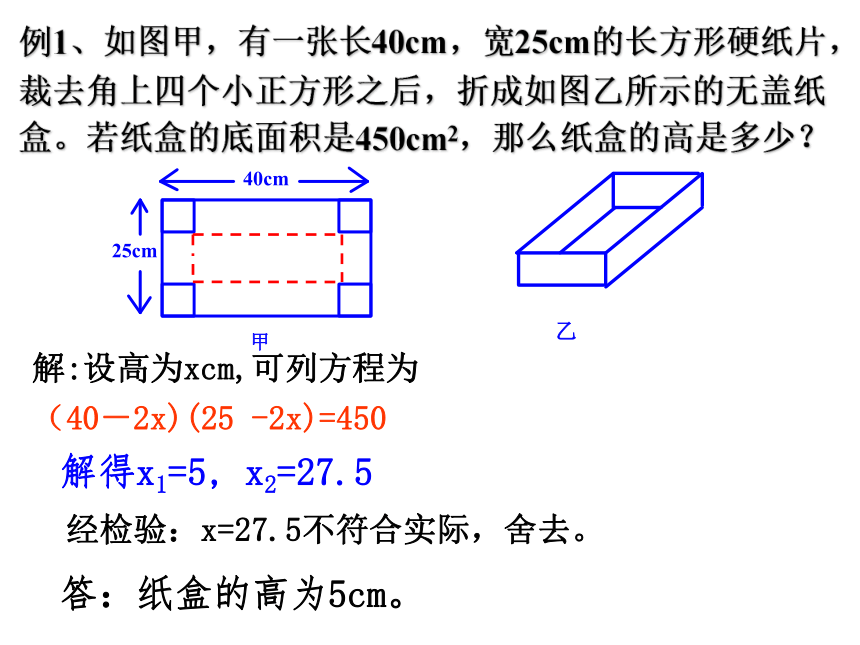
计算哪些量？例1、如图甲，有一张长40cm，宽25cm的长方形硬纸片，裁去角上四个小正方形之后，折成如图乙所示的无盖纸盒。若纸盒的底面积是450cm2，那么纸盒的高是多少？解:设高为xcm,可列方程为
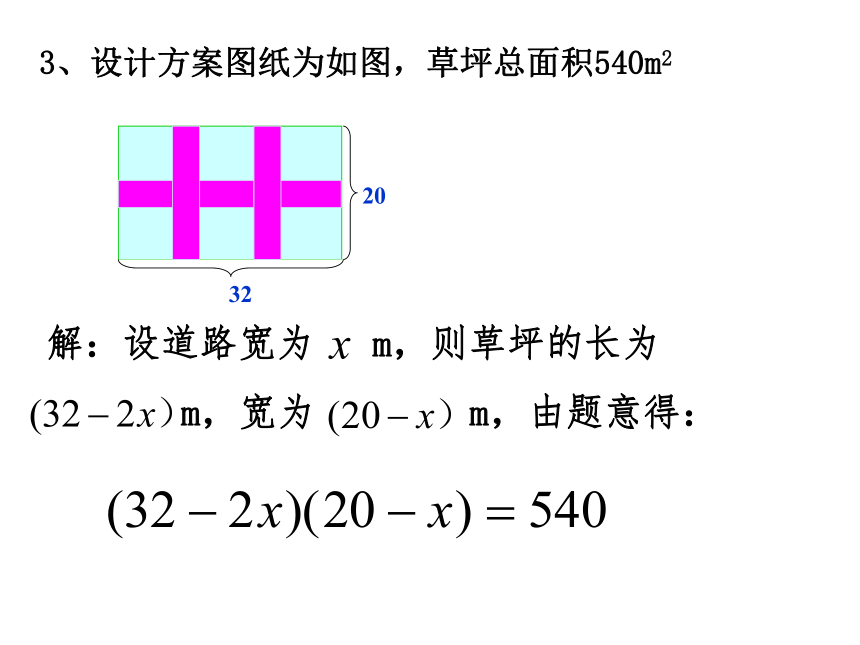
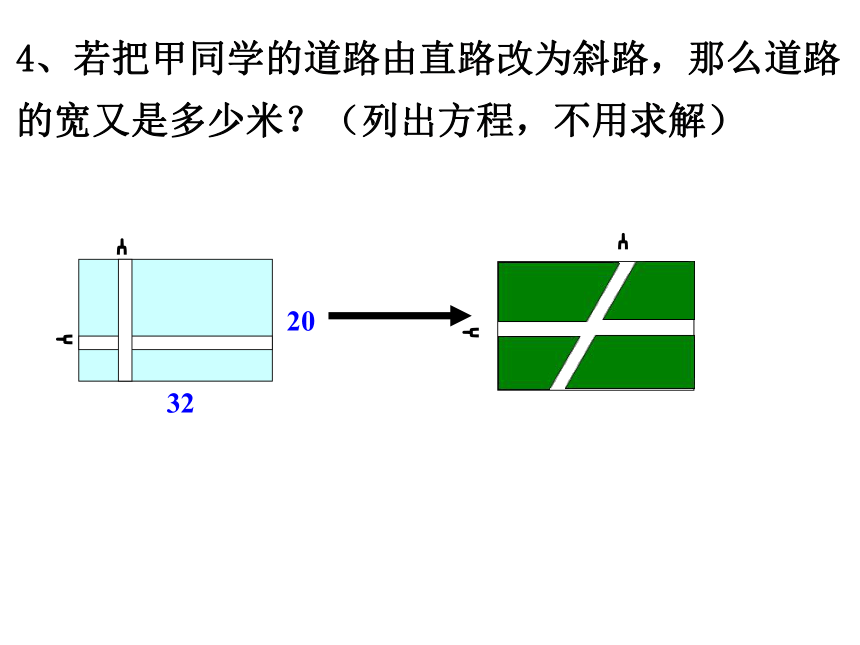
（40－2x)(25 -2x)=450解得x1=5, x2=27.5经检验：x=27.5不符合实际，舍去。答：纸盒的高为5cm。 取一张长与宽之比为5：2的长方形纸板，剪去四个边长为5cm的小正方形，并用它做一个无盖的长方体形状的包装盒。要使包装盒的容积为200cm3（纸板的厚度略去不计），问这张长方形纸板的长与宽分别为多少cm？试一试设长为5x，宽为2x，得：5（5x-10）（2x-10）=200例2、某中学为美化校园，准备在长32m，宽20m的长方形场地上，修筑若干条笔直等宽道路，余下部分作草坪，下面请同学们共同参与图纸设计，要求草坪面积为540m2求出设计方案中道路的宽分别为多少米？答：道路宽为1米。1、若设计方案图纸为如图，草坪总面积540m2长方形面积=长×宽分析：利用“图形经过平移”，它的面积大小不会改变的道理，把纵横两条路平移一下2、设计方案图纸为如图，草坪总面积540m2答：道路宽为2米。32203、设计方案图纸为如图，草坪总面积540m232204、若把甲同学的道路由直路改为斜路，那么道路的宽又是多少米？（列出方程，不用求解）3220鲜花为你盛开，你一定行！ON如图，红点从O出发，以3米/秒的速度向东前进，
经过t秒后，红点离O的距离ON= .（1） 3t|40-3t|NN鲜花为你盛开，你一定行！ONM北东如图，蓝、红两点同时从O点出发，红点以3米/秒的速度向东前进，蓝点以2米/秒的速度向北前进，经过t秒后，两点的距离MN 是 （代数式表示）（3） （4） BO=30米，CO=40米，蓝从B点，红从C点同时出发，其他条件不变，经过t秒后，两点的距离MN的距离是 （代数式表示） ONM北东BCONM北东ONM北东ONM北东BCBCBCBO=30米，CO=40米，蓝从B点，红从C点同时出发，其他条件不变，经过t秒后，两点的距离MN的距离是 （代数式表示）合作学习 一轮船以30km/h的速度由西向东航行在途中接到台风警报,台风中心正以20km/h的速度由南向北移动,已知距台风中心200km的区域(包括边界)都属于受台风影响区,当轮船接到台风警报时,测BC=500km,BA=300km.(1)图中C表示什么?B表示什么?圆又表示什么?(2)△ABC是什么三角形？能求出AC吗？(3)显然当轮船接到台风警报时,
没有受到台风影响，为什么？台风影响区域轮船台风中心直角三角形AC=400kmBC＞200km (5)在这现象中存在哪些变量?合作学习 一轮船以30km/h的速度由西向东航行在途中接到台风警报,台风中心正以20km/h的速度由南向北移动,已知距台风中心200km的区域(包括边界)都属于受台风影响区,当轮船接到台风警报时,测BC=500km,BA=300km.(4) 船是否受到台风影响与什么有关?船的航向，速度以及台风的行进方向和速度船、台风中心离A点的距离(6)若设经过t小时后,轮船和台风中心位置分别在B1和C1的位置那么如何表示B1C1？(7)当船与台风影响区接触时B1C1符合什么条件？（8）船会不会进入台风影响区？如果你认为会进入，那么从接到警报开始，经过多少时间就进入影响区？　B1C12=AC12+AB12B1C1=200km解:设当轮船接到台风警报后,经过t小时,则令：
(400-30t)2+(300-20t)2=2002问：(1) 这方程解得的t1,t2的实际意义是什么？(2) 从t1,t2的值中，还可得到什么结论？解得：t1≈8.35 t2≈19.34(3) 如何才能避免轮船不进入台风影响区？合作学习轮船首次受到台风影响的时间和最后受到影响的时间假如轮船一直不改变航向或速度，从开始到结束影响的总时间改变航向或速度（4）如果船速为10 km/h,结果将怎样?解:设当轮船接到台风警报后,经过t小时,则令：
(400-10t)2+(300-20t)2=2002化简，得：t2-40t+420=0
∵b2-4ac=(-40)2-4×1×420=-80<0∴此方程无实数根∴轮船继续航行不会受到台风的影响。谈谈这节课的学习体会练习：1、围绕长方形公园的栅栏长280m.已知该公园的面积为4800m2.求这个公园的长与宽. 练习：2、如图，斜靠在墙上的一根竹竿长AB=6.5m，BC=2.5m，若A端沿垂直于地面的方向AC下滑1m，问B端将沿CB方向移动多少m？ABC练习：3、如图，斜靠在墙上的一根竹竿长AB=6.5m，BC=2.5m，若A端沿垂直于地面的方向AC下滑1m，问B端将沿CB方向移动多少m？ABCA’B’4、如图，在△ABC中，∠B=90o。点P从点A开始沿边AB向点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边BC向点C以2cm/s的速度移动。如果P、Q分别从A，B同时出发，经过几秒，
△ PBQ的面积等于8cm2 ？解：设经过x秒，得：∴（6-x）×2x÷2=8∵ S△PBQ=BP×BQ÷2BP=6-x，BQ=2x解得：x1=2，x2=4练习： 某租赁公司拥有汽车100辆。据统计，当每辆车的月租金为3000元时，可全部租出。每辆车的月租金每增加50元，未租出的车将增加1辆。租出的车每辆每月的维护费为150元，未租出的车每辆每月只需维护费50元。(1)当每辆车的月租金定3600元时,能租出多少辆?(2)当每辆车的月租金定为多少元时，租赁公司的月收益(租金收入扣除维护费)可达到306600元?课外拓展100-（3600-3000）÷50=88（辆）设月租金定为x元，得：化简，得：x2-8100x+16380000=0∴x1=3900，x2=4200