2.2一元二次方程的解法（4）.

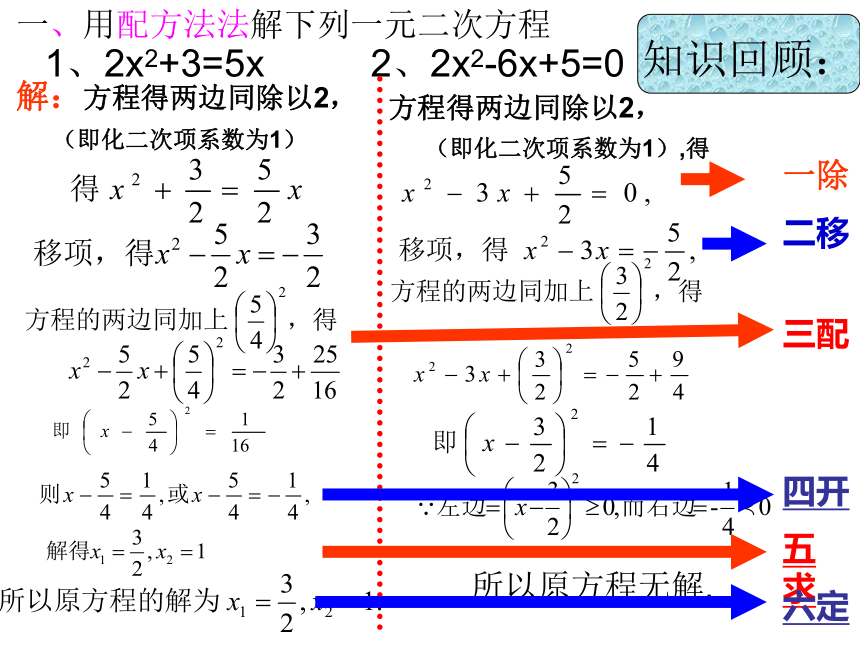
课件19张PPT。泰顺六中 翁怀新2014年3月12日2.2一元二次方程的解法（4）一、用配方法法解下列一元二次方程1、2x2+3=5x 2、2x2-6x+5=0解：方程得两边同除以2，
（即化二次项系数为1） 方程得两边同除以2，
（即化二次项系数为1）,得 所以原方程无解.一除二移三配四开五求六定知识回顾：
★一除、二移、三配、四开、五解、六定.“配方法”解一元二次方程的基本步骤：(1)除a：把二次项系数化为“1”(方程的两边同时除以二次项系数a)
(2)移项:把常数项移到方程的右边;
(3)配方:方程两边都加上一次项系数一半的平方;
(4)开方:根据平方根意义,方程两边开平方;
(5)求解:解两个一元一次方程;
(6)定解:写出原方程的解.
二、用配方法解一元二次方程的基本步骤：（一般形式：ax2+bx+c=0，a ≠ 0）4.用开平方法，解得答案。第①步当二次项系数不是1时，把方程两边同时除以 , a第②步把_________移到方程的右边 常数项第③步等式两边同时加上____________________
一次项系数一半的平方;第④步用“ 法”解二元一次方程。开平方为什么要，？若，则方程__ _实数 解无二、用配方法解一元二次方程的基本步骤：（一般形式：ax2+bx+c=0，a ≠ 0）当 b2-4ac≥0时，特别提醒：
这是为什么？ 当 b2-4a<0时，原方程没有实数根二、用配方法解一元二次方程的基本步骤：（一般形式：ax2+bx+c=0，a ≠ 0）


特别提醒：
这是为什么？一元二次方程的求根公式（1） （2）（3） 例8、用公式法解下列一元二次方程（4）2x2-6x+5=0解:（1） a=2,b=-5,c=3,
b2-4ac=(-5)2-4x2x3=1>0确定系数计算代入定根三、精讲例题（1） （2）（3） 例8、用公式法解下列一元二次方程（4）2x2-6x+5=0 a=4,b=4,c=1,
b2-4ac=42-4x4x1=0计算代入定根确定系数(2)移项,得4x2+4x+1=0变形三、精讲例题（1） （2）（3） 例8、用公式法解下列一元二次方程（4）2x2-6x+5=0 a=3,b=-8,c=-2,
b2-4ac=（-8）2-4x3x（-2）=88≥0(3)方程的两边同乘4,
得3x2 - 8x-2=0变形计算代入定根确定系数三、精讲例题（1） （2）（3） 例8、用公式法解下列一元二次方程（4）2x2-6x+5=0解:（4） a=2,b=-6,c=5,确定系数计算所以原方程没有实数根,即无解.b2-4ac=(-6)2-4x2x5=-4<0
三、精讲例题归纳小结：从一元二次方程的一般形式为ax2+bx+c=0 (a≠0)的求根公式的推导过程中不难看出，方程的根的情况由代数式b2-4ab的值来决定。因此b2-4ab叫做一元二次方程的判别式，它的值与一元二次方程的根的关系是：b2-4ab>0 方程ax2+bx+c=0 (a≠0)
有两个不相等的实数根； b2-4ab< 0 方程ax2+bx+c=0 (a≠0)
没有实数根； b2-4ab=0 方程ax2+bx+c=0 (a≠0)
有两个相等的实数根；1、用判别式判别下列方程根的情况（不要求解方程）；
（1）2x2-3x+1=0 解:（1）b2-4ac=(-3)2-4x2x1=1>0方程ax2+bx+c=0 (a≠0)有两个不相等的实数根；方程ax2+bx+c=0 (a≠0)有两个相等的实数根方程ax2+bx+c=0 (a≠0)没有实数根；4、练习:用公式法解方程
（1） x2 - x -1= 0
（2） x2 - 2 x+2= 02、方程3 x2 +1=2 x中， b2-4ac=_____.
3、若关于x的方程x2-2nx+3n+4=0
有两个相等的实数根，则n=_________ .0-1或4（x1 = 1x2 =- --）（x1 = x2 = ）例9、解方程即x1=4,x2=2想一想：
你能用因式分解法解本例的方程？三、精讲例题例9、解方程解得x1=4,x2=2三、精讲例题用“公式法”解一元二次方程的解题步骤：
（一元二次方程的一般形式为ax2+bx+c=0)(1)变形：把方程化为一般形式；(3)计算：求出b2-4ab的值;(4)代入：把有关数值代入公式计算
（若b2-4ab≥0，把a、b、c及b2-4ab的值代入一元二次方程的求 根公式，求出方程的根；若b2-4ab<0，此时方程无实数根）；(2)确定系数：用a、b、c写出各项系数；(5)定根：写出原方程的根。1、用公式法解下列一元二次方程 （2）（1）（2）（4）2、用适当方法解下列一元二次方程（1）四、当堂训练注意：一元二次方程有实数根；说明方程有两个不相等的实数根或两个相等的实数根的两种情况。
五、拓展延伸 1、m取什么值时，方程 x2+(2m+1)x+m2-4=0
有两个实数根？解：b2-4ac=(2m+1)2-4x1x(m2-4)=4m+17≥0 布置作业：
1.作业本(2分册2.2(3)（p.9-10.)
2.课时特训A类做第1到14题；
B类做第1到8题；
C类做1到6题(p.25-27.) 再见