一元二次方程复习

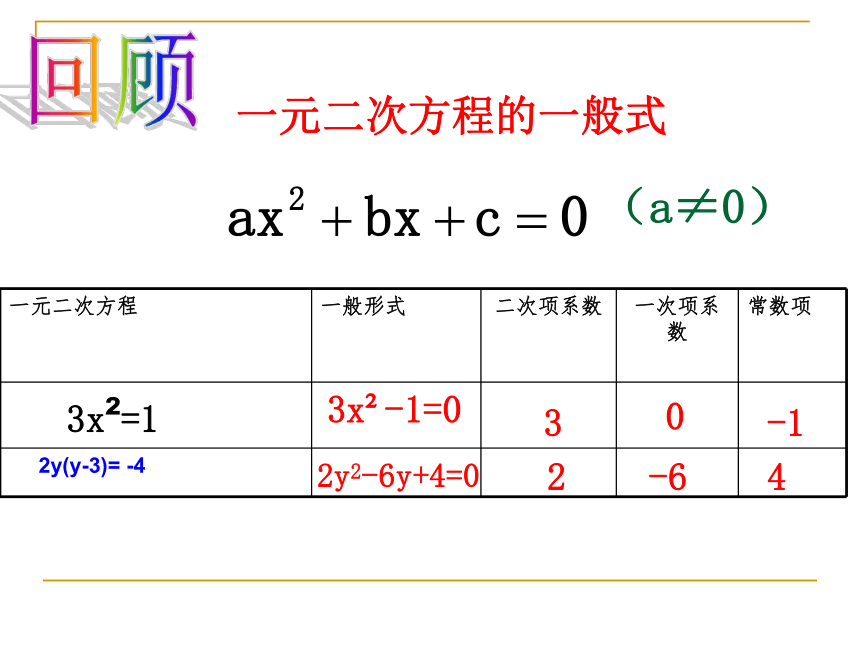
课件39张PPT。一元二次方程复习一元二次方程一元二次方程的定义一元二次方程的解法一元二次方程的应用方程两边都是整式ax2+bx+c=0（a?0）本章知识结构只含有一个未知数未知数的最高次数是2配方法直接开平方法因式分解法二次项系数为1，而一次项系数为偶数 公式法二次项系数为1，而一次项系数为偶数二次项系数为1，而一次项系数为偶数一元二次方程根与系数的关系　　判断下列方程是不是一元二次方程，若不是一元二次方程，请说明理由？1、(x－1)２＝４　 ２、x2－2x=４、x２＝y+１　5、x３－２x２＝１6、ax2 + bx + c＝１×√√×××（a≠0）一元二次方程的定义一元二次方程的一般式（a≠0） 3x2-1=032-6-140回顾2y2-6y+4=02≠－ 2填一填3、关于x的方程
（k2+2k-3)x2 + (k-1)x + 5 = 0 ,
(1)k为何值时，方程是一元一次方程？
(2)k为何值时，方程是一元二次方程？用适当的方法解下列方程一元二次方程的解法规律： ① 一般地，当一元二次方程一次项系数为0时（ax2+c=0），应选 ；
②若常数项为0(ax2+bx=0),应选用 ；
③若一次项系数和常数项都不为0 (ax2+bx+c=0），先化为一般式，看一边的整式是否容易因式分解，若容易，宜选用 ，不然选用 ；
④不过当二次项系数是1，且一次项系数是偶数时，用 也较简单。直接开平方法因式分解法因式分解法公式法配方法比一比，看谁做得快：(1) 4(t+2 )2=3
(2)3t(t+2)=2(t+2)
(3)(y+ )(y- )=2(2y-3)
(4)-5x2-7x+6=0
(5)x2+2x-9999=0提高：为了解方程（y2-1）2 -3（y2-1）+2=0，我们将y2-1视为一个整体，解：设 y2-1=a，则
（y2-1）2=a2，
a2 - 3a+2=0， （1）
a1=1，a2=2。
当a=1时，y2 -1=1，y =± ，
当a=2时，y2-1=2，y=±
所以y1= ，y2 =- y 3= y4= -解答问题：1、在由原方程得到方程（1）的过程中，利用了 法达到了降次的目的，体现了 的数学思想。
换元转化2. 解方程

(x-2)2+3(x-2)-10=03.已知(a2+b2)2-(a2+b2)-6=0,
求a2+b2的值。1、如果等腰三角形的三条边长是
x2-6x+5=0的根，则这个等腰三角形的周长是--------
2、设（3a+3b-2)(3a+3b+1)=16 , 则a+b的值是-------
3.构造一个一元二次方程，要求：
（1）常数项为零（2）有一根为2。
再接再励△≥0<=>有两个实数根△＞0<=>有两个不等实数根△=0<=>有两个相等实数根△＜0<=>无实根 根的判别式
一元二次方程aX2+bx+c=0(a≠0)（△=b2-4ac） 一元二次方程根与系数的关系如果一元二次方程ax2+bx+c=0（a=0）的两个根是x1，x2 那么x1+x2=-—
x1.x2= —
abac 如果一元二次方程x2+px+q=0的两个根是x1，x2 那么
x1+x2=-p
x1.x2= q 韦达定理
例1：
关于x的方程有两个不相等的实数根，求k的取值范围。解：∵△＞０
解得k＞０＞０∴
又∵k-1≠0
∴k＞０且k≠0
说一说：下面解法正确吗？忽视二次项
系数不为0例2、求证：关于x的方程：


有两个不相等的实根。证明： 所以，无论m取任何实数,方程有两个不相等的实数根。即：△>0证明： 即：△>0反思－提高： 1.已知一直角三角形的三边为请你判断关于的方程的根的情况。 》》2.若关于x的方程x2+2(k+2)x+k2＝0 两个实数根之和大于-4，求k的取值范围。 反思－提高： 例1. 某药品经过两次降价，每瓶零售价由100元降为81元，已知两次降价百分率相同，求两次降价的百分率。1、党的十六大提出全面建设小康社会，加快推进社会主义现代化，力争国民生产总值到2020年比2000年翻两番。本世纪的头二十年（2001年～2020年），要实现这一目标，以十年为单位，设每个十年的国民生产总值的增长率都是x，那么x满足的方程为 （ ）
A、(1+x)2=2 B、(1+x)2=4
C、1+2x=2 D、（1+x）+2（1+x)=4B关键是理解“翻两番”是原来的4倍，而不是原来的2倍。 相信自己 2.某电冰箱厂每个月的产量都比上个月增长的百分数相同。已知该 厂今年4月份的电冰箱产量为5万台，6月份比5月份多生产了12000 台，求该厂今年产量的月平均增长率为多少?面积体积类应用题： 例2、有一堆砖能砌12米长的围墙,现要围一个20平方米的鸡场,鸡场的一边靠墙(墙长7米),其余三边用砖砌成,墙对面开一个1米宽的门,求鸡场的长和宽各是多少米?解：设鸡场的宽为x米，则长为（12+1-2x）=（13-2x）米 列方程得：X（13-2x）=20解得：x1=4，x2=2.5经检验：两根都符合题意答：此鸡场的长和宽分别为5和4米或8与2.5米。∴13-2x=5或8解:设底边边长应增加xcm,
由题意,可列出方程_________________1、如图,礼品盒高为10cm,底面为正方形,边长为4cm,若保持盒子高度不变,问底边边长应增加多少厘米才能使其体积增加200cm3?10(x+4)2=10×42+200相信自己80cm50cm2、在一幅长80cm，宽50cm的矩形风景画的四周
镶一条金色纸边，制成一幅矩形挂图，如图所示，
如果使整个挂图的面积是5400cm2，设金边的宽为xcm，则列出的方程是 .（80+2x）（50+2x）=5400相信自己 3．某林场计划修一条长750m，断面为等腰梯形的渠道，断面面积为1.6m2，上口宽比渠深多2m，渠底比渠深多0.4m．
（1）渠道的上口宽与渠底宽各是多少？
（2）如果计划每天挖土48m3，需要多少天才能把这条渠道挖完？分析：因为渠深最小，为了便于计算，不妨设渠深为xm，则上口宽为x+2，渠底为x+0.4，那么，根据梯形的面积公式便可建模．例3、某商场的音响专柜,每台音响进价4000元,当售价定为5000元时,平均每天能售出10台,如果售价每降低100元,平均每天能多销售2台,为了多销售音响,使利润增加12%,则每台销售价应定为多少元?解得: x =200或 x=300每台的利润×售出的台数=总利润解:法二：设每天多销售了x台。
（10+x)(1000-50x)=10000(1+12%)ABCPQ（1）用含x的代数式表
示BQ、PB的长度；（2）当为何值时，△PBQ为等腰三角形；（3）是否存在x的值，使得四边形APQC的面积等于20cm2？若存在，请求出此时x的值；若不存在，请说明理由。1.如图，Rt△ABC中，∠B=90°，AC=10cm，BC=6cm，现有两个动点P、Q分别从点A和点B同时出发，其中点P以2cm/s的速度，沿AB向终点B移动；点Q以1cm/s的速度沿BC向终点C移动，其中一点到终点，另一点也随之停止。连结PQ。设动点运动时间为x秒。问(1)P、Q两点从出发开始几秒时,四边形PBCQ的面积是33c㎡
2.如图,已知A、B、C、D为矩形的四个顶点,AB=16㎝,AD=6㎝,动点P、Q分别从点A、C同时出发,点P以3㎝/s的速度向点B移动,一直到点B为止,点Q以2㎝/s的速度向点D移动. (2)P、Q两点从出发开始几秒时,
点P点Q间的距离是10㎝1.元旦期间，学校组织了一次集体活动,每两个人都要互赠礼物,统计本次活动参加的人共收到132件礼物.问参加的人数是多少?2、某人将2000元人民币按一年定期储蓄存入银行，到期后支取1000元用作购物，剩下的1000元及利息又全部按一年定期储蓄存入银行，若银行存款的利率不变，到期后得本利和共1320元（不计利息税），求一年定期存款的年利率。3.将一条长为56cm的铁丝剪成两段,并把每一段围成一个正方形.
(1).要使这两个正方形的面积之和等于100cm2,该怎样剪?
(2).要使这两个正方形的面积之和等于196cm2,该怎样剪?
(3).这两个正方形的面积之和可能等于200m2吗?
将一条长为56cm的铁丝剪成两段,并把每一段围成一个正方形.
(1).要使这两个正方形的面积之和等于100cm2,该怎样剪?
(2).要使这两个正方形的面积之和等于196cm2,该怎样剪?
(3).这两个正方形的面积之和可能等于200m2吗?
将一条长为56cm的铁丝剪成两段,并把每一段围成一个正方形.
(1).要使这两个正方形的面积之和等于100cm2,该怎样剪?
(2).要使这两个正方形的面积之和等于196cm2,该怎样剪?
(3).这两个正方形的面积之和可能等于200m2吗?
你说我说大家说：
通过今天的学习你有什么收获或感受？一元二次方程一元二次方程的定义一元二次方程的解法一元二次方程的应用方程两边都是整式ax2+bx+c=0（a?0）本章知识结构只含有一个未知数求知数的最高次数是2配 方 法求 根 公式法直接开平方法因 式 分解法二次项系数为1，而一次项系数为偶数再见！2.在直角梯形ABCD中，AD∥BC，∠C=90°，BC=16，AD=21，DC=12，动点P从点D出发，沿线段DA方向以每秒2个单位长度的速度运动，动点Q从点C出发，沿线段CB 以每秒1个单位长度的速度向点B运动. 点P、Q分别从点D、C同时出发，当点P运动到点A时，点Q随之停止运动，设运动时间为t秒.
问:当t为何值时，△BPQ是等腰三角形？ADBCPQ分类讨论思想