2.3一元二次方程的应用（1）

课件13张PPT。泰顺六中 翁怀新2014年3月14日2.3一元二次方程的应用（1）1.已知两个连续正奇数的积等于143,应用一元二次方程
求这两个数.引例：解：设较小的一个奇数为x,则另一个数为x+2.根据题意列方程得：x(x+2)=143解得：x1=11,x2=-13经检验,x2=-13不符合题意，舍去。答：这两个数奇数是11和13.你能总结出列一元二次方程解应用题的步骤？列方程解应用题的基本步聚1、审：弄清题意，找出题中的等量关系;2、设：设未知数，包括直接设未知数或间接设未知数;3、列：根据等量关系列出方程;4、解：解方程，并检验根是否符合实际意义;5、查与答：检查求出的值是否符合实际意义，
回答题中所问;回顾：特别注意：列一元二次方程解应用题时，由于所得根
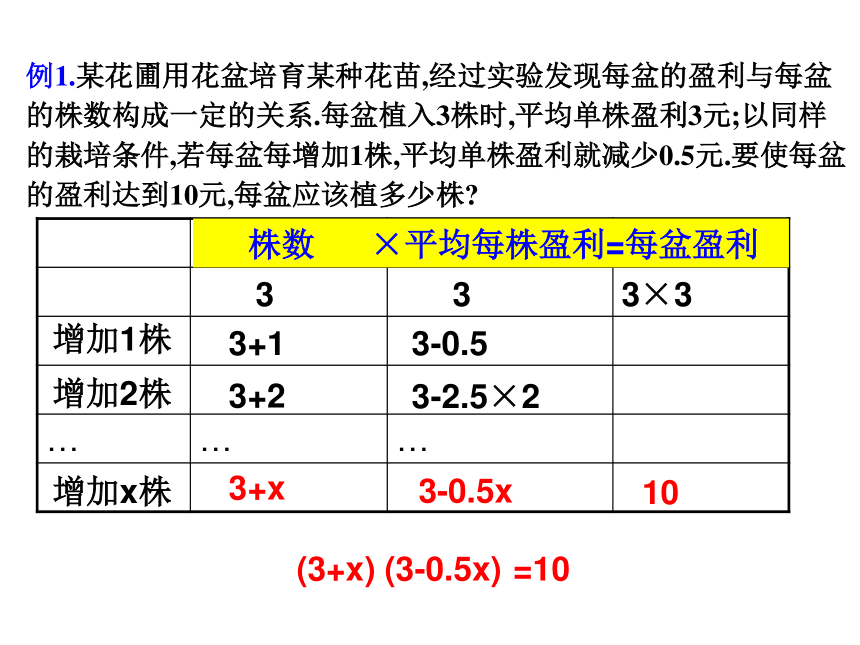
一般有两个，所以要检验这两个根是否符合问题的要求。例1.某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?分析: 本题涉及的主要数量有每盆的花苗株数,平均单株盈利,每盆花苗的盈利.
主要数量关系有:
平均单株盈利×株数=每盆盈利;
平均单株盈利=3-0.5×每盆增加的株数.株数平均每株盈利每盆盈利 株数 ×平均每株盈利=每盆盈利333×3增加1株3+13-0.5增加2株3+23-2.5×2增加x株3+x3-0.5x10例1.某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?(3+x)(3-0.5x)=10解：设每盆增加x株.3+x=4， 3+x=5答：每盆应该植4或5株间接设元法练习：书38页作业题1某超市销售一种饮料，平均每天可售出100箱，每箱利润120元．为了扩大销售，增加利润，超市准备适当降价．据测算，若每箱降价1元，每天可多售出2箱．如果要使每天销售饮料获利14000元，问每箱应降价多少元？ 此题利用的数量关系是： 销售每箱饮料的利润×销售总箱数=销售总利润， 解：设要使每天销售饮料获利14000元，每箱应降价x元，
依据题意列方程得，（120-x）（100+2x）=14000，整理得x2-70x+1000=0， 解得x1=20，x2=50；答：每箱应降价20元或50元，可使每天销售饮料获利14000元 提升：同时为了减少库存，那应降价多少？当x=20时，每天可售出100+2x=140箱。当x=50时，每天可售出100+2x=200箱。∵200>140, ∴应降价50元。直接设元法1.某公司今年的销售收入是a万元，如果每年的增长率都是x，那么一年后的销售收入将达到____ _ _万元（用代数式表示）2.某公司今年的销售收入是a万元，如果每年的增长率都是x，那么两年后的销售收入将达到__ ____万元（用代数式表示）3.某试验田去年亩产1000斤，今年比去年增产10%，则今年
亩产为___________斤,计划明年再增产10%，则明年的产量
为 斤。
4.某厂一月份产钢50吨，二、三月份的增长率都是x，则该厂
三月分产钢______________吨.1100121050(1+x)2（1）增长率问题 （2）降低率问题 分类归纳：例2.根据如下图的统计图，求2008到2010年，我国风电新增装机容量的平均年增长率（精确到0.1%)例2.根据如下图的统计图，求2008到2010年，我国风电新增装机容量的平均年增长率（精确到0.1%)解：设2008到2010年我国风电新增装机容量的平均年增长率x,由题意可以列出方程，得615（1+ )2-1893解这个方程，得小结：1、平均增长（降低）率公式：a(1+x)2=b2、注意：
解这类问题列出的方程一般
用 直接用开平方法 布置作业：
1.作业本(1分册2.2(3)（p.10-11.)
2.课时特训A类做第1到14题；
B类做第1到8题；
C类做1到6题(p.25-27.) 再见