2022-2023学年浙教版数学九年级下册3.1.2 中心投影 课件 (共29张PPT)
文档属性
| 名称 | 2022-2023学年浙教版数学九年级下册3.1.2 中心投影 课件 (共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 908.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 09:10:56 | ||
图片预览







文档简介
(共29张PPT)
3.1 投影
第2课时 中心投影
掌握中心投影概念及不同位置的中心投影所形成的投影特征.
可以根据题意画出简单的中心投影.
可以根据中心投影的特点进行简单的计算.
掌握中心投影和平行投影的区别和联系.
学习目标
皮影
手影
在生活中,我们可以看到各种各样的影子.
皮影和手影是投影吗?
是平行投影吗?
情境导入
由同一点出发的投射线所形成的投影叫做中心投影.
皮影和手影都属于中心投影.
由于中心投影的投射线和平行投影的投射线具有不同的性质,因此,在两种投影下,物体的影子有明显的差别.
新知学习
这个“点”就是中心,相当于物理上学习的“点光源”.
新知讲解
由同一点出发的投射线所形成的投影叫做中心投影.
1.取一些长短不等的小棒和三角形、矩形纸片,用手电筒(或台灯)等去照射这些小棒和纸片,观察它们的影子.
合作探究
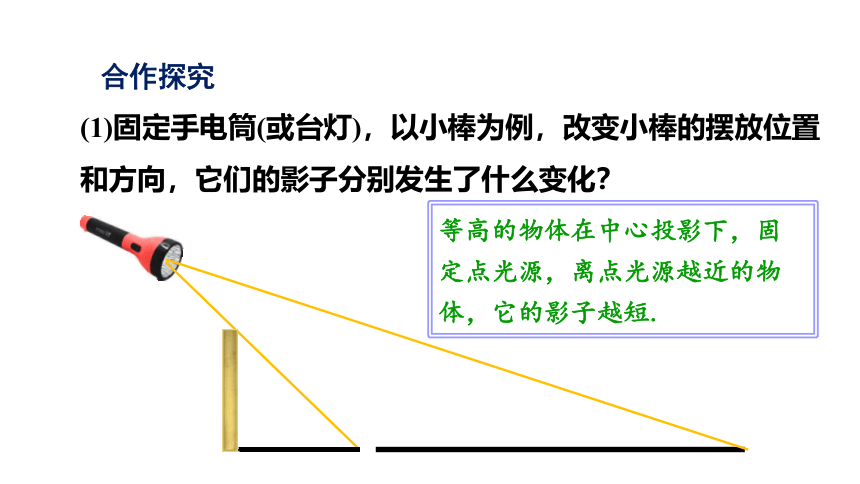
(1)固定手电筒(或台灯),以小棒为例,改变小棒的摆放位置和方向,它们的影子分别发生了什么变化?
合作探究
等高的物体在中心投影下,固定点光源,离点光源越近的物体,它的影子越短.
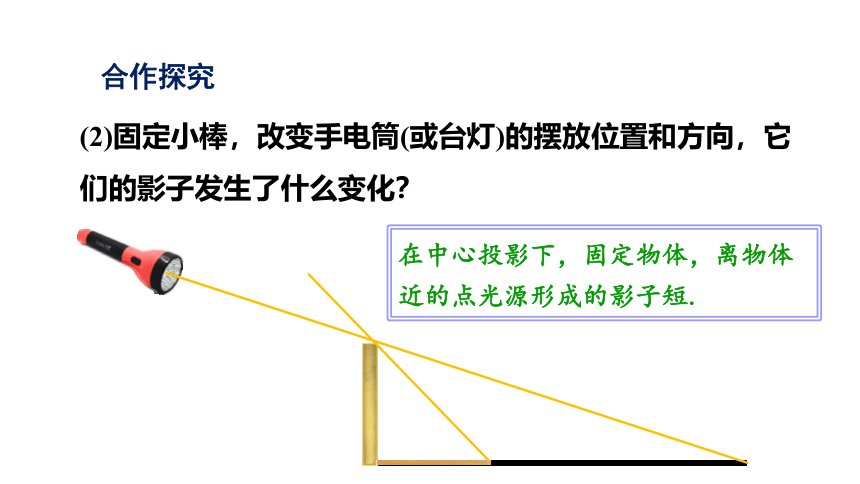
(2)固定小棒,改变手电筒(或台灯)的摆放位置和方向,它们的影子发生了什么变化?
合作探究
在中心投影下,固定物体,离物体近的点光源形成的影子短.
注意:
(1)在中心投影中,若不改变物体的位置,只改变投影方向,物体的影子会随着投影方向的改变而改变;
(2)中心投影发出的光线是发散的,不平行的.
A
H
A'
2.(1)想一想,点A在投影面H内的中心投影是什么图形?
一个点的中心投影还是一个点.
O(光源)
合作探究
A
H
B
A′
B′
O(光源)
(2)取一根细竹签,在灯泡和桌面的位置都相对固定时,观察在灯光下竹签投到桌面上的影子,竹签的影子是什么形状?它们的长是否相等?然后改变竹签与桌面所成的角度,它的影子的形状和大小是否发生了变化?
合作探究
当线段AB与投影面平行时,AB的中心投影A′B′把线段AB放大了,且AB∥A′B′,△OAB∽△OA′B′.
A
H
B
A′
B′
O(光源)
合作探究
(2)取一根细竹签,在灯泡和桌面的位置都相对固定时,观察在灯光下竹签投到桌面上的影子,竹签的影子是什么形状?它们的长是否相等?然后改变竹签与桌面所成的角度,它的影子的形状和大小是否发生了变化?
线段A′B′的长度可能大于AB,可能等于AB,也可能小于AB,改变线段AB与投影面所成的角度,它的投影A′B′的长度会发生变化.
A
H
B
A′
(B′)
O(光源)
合作探究
(2)取一根细竹签,在灯泡和桌面的位置都相对固定时,观察在灯光下竹签投到桌面上的影子,竹签的影子是什么形状?它们的长是否相等?然后改变竹签与桌面所成的角度,它的影子的形状和大小是否发生了变化?
当线段AB的端点在同一条投射线上时,点A,B在投影面H内的投影A′,B′重合.这时线段AB在面H内的投影是一个点.
(3)取一张平行四边形的纸片,在灯泡和桌面位置都固定时,观察纸片在灯光下投在桌面上影子的形状,并比较纸片的面积与影子面积的大小.由此思考:一个平行四边形的中心投影是什么图形?平行四边形的面积与它的中心投影的面积的大小有怎样的关系?
合作探究
如图,当□ABCD平行于投影面H时,它在面H内的投影和□ABCD是位似图形,位似中心是点O.此时投影的面积大于平行四边形的面积(图①);
合作探究
合作探究
当平行四边形倾斜于投影面时,投影A′B′C′D′的形状和大小会发生改变,可能是与它不相似的四边形(图②),它的面积和□ABCD的面积大小不能确定.投影还可能是一条线段(图③),但不会是一个点.
例1 如图,下面两幅图表示两根标杆在同一时刻的投影.在图中画出形成投影的光线.它们是平行投影还是中心投影?请说明理由.若是中心投影,请找出点光源.
(1)
(2)
例题讲解
解:分别连结标杆的顶端与其投影上的对应点.
很明显,图(1)的投射线互相平行,是平行投影.
图(2)的投射线将相交于一点,是中心投影.
(1)
(2)
例题讲解
平行投影
中心投影
(1)
(2)
例题讲解
平行投影
中心投影
投射线相交的点即为点光源.
因为点光源、物体上的点及物体在影子上的对应点在同一条直线上,要确定点光源的位置,应先找出物体上的两个点及其影子上的对应点,再分别过物体上的点和影子上的对应点作直线,两条直线的交点即为点光源.
确定中心投影的点光源的方法
例题讲解
例2 如图,树AB在路灯O的照射下形成投影AC.已知树高AB=2m,树影AC=3m,树与路灯的水平距离AP=45m.求路灯的高度OP.
解:如图,可知△ABC∽△POC,
则,即.
解得PO=5.
答:路灯的高度OP是5m.
平行投影 中心投影
区别 光源
投射线
特征
平行投影与中心投影的区别与联系
太阳等
平行
点光源(如台灯等)
从同一点出发
(1)影长与物高不一定成比例;
(2)影子的方向由点光源与物体的相对位置确定
同一时刻、同一地点,平行投影下不同物体的影长与物高成比例,且影子的方向总相同
平行投影 中心投影
区别 物体与投影面平行时
联系 平行投影与中心投影的区别与联系
离点光源越近,影子越大;离点光源越远,影子越小
影子与物体全等
都是物体在光线的照射下在某个平面内形成的影子,即都是投影
2.举例说明生活中的中心投影现象.
解:路灯,手电筒照射物体时投影面出现影子.
1.下列各种现象属于中心投影现象的是( )
A.上午10点时,走在路上的人的影子
B.晚上10点时,走在路灯下的人的影子
C.中午用来乘凉的树影
D.升国旗时,地上旗杆的影子
B
随堂练习
3.两棵小树在一盏路灯下的影子如图所示.
(1)确定该路灯灯泡所在的位置;
(2)画出图中表示婷婷影长的线段.
解:(1)如图所示,点O就是路灯灯泡所在的位置.
(2)如图所示,表示婷婷影长的线段为CD.
A
B
C
D
O
随堂练习
随堂练习
4.如图,路边有一盏路灯.
长度相同的两根竹竿在这盏路灯下的影子一定一样长吗?如果不一定,那么什么情况下它们的影子一样长?
解:
不一定.
当它们到这盏路灯的距离一样时,它们的影子一样长.
解:如图,A为灯泡,EB为桌面半径,DC为桌面影子的半径.
∴AE=2.5,ED=1.2,EB=0.5.
∵EB∥DC,∴,
随堂练习
5.现有直径为1m的圆桌面,桌脚高1.2m(不计桌面厚度).如图所示,在桌面正上方2.5m处有一盏灯.你能测算出晚上开灯后圆桌面在地面上的影子的面积吗? (取π=3.14,精确到0.1m)
∴DC=·AD=(2.5+1.2)=0.74.
S影子=π×(0.74)2≈3.14×0.55≈1.7(m2).
∴圆桌面在地面上的影子的面积
是1.7 m2.
随堂练习
5.现有直径为1m的圆桌面,桌脚高1.2m(不计桌面厚度).如图所示,在桌面正上方2.5m处有一盏灯.你能测算出晚上开灯后圆桌面在地面上的影子的面积吗? (取π=3.14,精确到0.1m)
课堂小结
本节课学习了哪些内容?
1.中心投影的概念及特点.
2.中心投影的画法和计算.
3.平行投影和中心投影的区别与联系.
3.1 投影
第2课时 中心投影
掌握中心投影概念及不同位置的中心投影所形成的投影特征.
可以根据题意画出简单的中心投影.
可以根据中心投影的特点进行简单的计算.
掌握中心投影和平行投影的区别和联系.
学习目标
皮影
手影
在生活中,我们可以看到各种各样的影子.
皮影和手影是投影吗?
是平行投影吗?
情境导入
由同一点出发的投射线所形成的投影叫做中心投影.
皮影和手影都属于中心投影.
由于中心投影的投射线和平行投影的投射线具有不同的性质,因此,在两种投影下,物体的影子有明显的差别.
新知学习
这个“点”就是中心,相当于物理上学习的“点光源”.
新知讲解
由同一点出发的投射线所形成的投影叫做中心投影.
1.取一些长短不等的小棒和三角形、矩形纸片,用手电筒(或台灯)等去照射这些小棒和纸片,观察它们的影子.
合作探究
(1)固定手电筒(或台灯),以小棒为例,改变小棒的摆放位置和方向,它们的影子分别发生了什么变化?
合作探究
等高的物体在中心投影下,固定点光源,离点光源越近的物体,它的影子越短.
(2)固定小棒,改变手电筒(或台灯)的摆放位置和方向,它们的影子发生了什么变化?
合作探究
在中心投影下,固定物体,离物体近的点光源形成的影子短.
注意:
(1)在中心投影中,若不改变物体的位置,只改变投影方向,物体的影子会随着投影方向的改变而改变;
(2)中心投影发出的光线是发散的,不平行的.
A
H
A'
2.(1)想一想,点A在投影面H内的中心投影是什么图形?
一个点的中心投影还是一个点.
O(光源)
合作探究
A
H
B
A′
B′
O(光源)
(2)取一根细竹签,在灯泡和桌面的位置都相对固定时,观察在灯光下竹签投到桌面上的影子,竹签的影子是什么形状?它们的长是否相等?然后改变竹签与桌面所成的角度,它的影子的形状和大小是否发生了变化?
合作探究
当线段AB与投影面平行时,AB的中心投影A′B′把线段AB放大了,且AB∥A′B′,△OAB∽△OA′B′.
A
H
B
A′
B′
O(光源)
合作探究
(2)取一根细竹签,在灯泡和桌面的位置都相对固定时,观察在灯光下竹签投到桌面上的影子,竹签的影子是什么形状?它们的长是否相等?然后改变竹签与桌面所成的角度,它的影子的形状和大小是否发生了变化?
线段A′B′的长度可能大于AB,可能等于AB,也可能小于AB,改变线段AB与投影面所成的角度,它的投影A′B′的长度会发生变化.
A
H
B
A′
(B′)
O(光源)
合作探究
(2)取一根细竹签,在灯泡和桌面的位置都相对固定时,观察在灯光下竹签投到桌面上的影子,竹签的影子是什么形状?它们的长是否相等?然后改变竹签与桌面所成的角度,它的影子的形状和大小是否发生了变化?
当线段AB的端点在同一条投射线上时,点A,B在投影面H内的投影A′,B′重合.这时线段AB在面H内的投影是一个点.
(3)取一张平行四边形的纸片,在灯泡和桌面位置都固定时,观察纸片在灯光下投在桌面上影子的形状,并比较纸片的面积与影子面积的大小.由此思考:一个平行四边形的中心投影是什么图形?平行四边形的面积与它的中心投影的面积的大小有怎样的关系?
合作探究
如图,当□ABCD平行于投影面H时,它在面H内的投影和□ABCD是位似图形,位似中心是点O.此时投影的面积大于平行四边形的面积(图①);
合作探究
合作探究
当平行四边形倾斜于投影面时,投影A′B′C′D′的形状和大小会发生改变,可能是与它不相似的四边形(图②),它的面积和□ABCD的面积大小不能确定.投影还可能是一条线段(图③),但不会是一个点.
例1 如图,下面两幅图表示两根标杆在同一时刻的投影.在图中画出形成投影的光线.它们是平行投影还是中心投影?请说明理由.若是中心投影,请找出点光源.
(1)
(2)
例题讲解
解:分别连结标杆的顶端与其投影上的对应点.
很明显,图(1)的投射线互相平行,是平行投影.
图(2)的投射线将相交于一点,是中心投影.
(1)
(2)
例题讲解
平行投影
中心投影
(1)
(2)
例题讲解
平行投影
中心投影
投射线相交的点即为点光源.
因为点光源、物体上的点及物体在影子上的对应点在同一条直线上,要确定点光源的位置,应先找出物体上的两个点及其影子上的对应点,再分别过物体上的点和影子上的对应点作直线,两条直线的交点即为点光源.
确定中心投影的点光源的方法
例题讲解
例2 如图,树AB在路灯O的照射下形成投影AC.已知树高AB=2m,树影AC=3m,树与路灯的水平距离AP=45m.求路灯的高度OP.
解:如图,可知△ABC∽△POC,
则,即.
解得PO=5.
答:路灯的高度OP是5m.
平行投影 中心投影
区别 光源
投射线
特征
平行投影与中心投影的区别与联系
太阳等
平行
点光源(如台灯等)
从同一点出发
(1)影长与物高不一定成比例;
(2)影子的方向由点光源与物体的相对位置确定
同一时刻、同一地点,平行投影下不同物体的影长与物高成比例,且影子的方向总相同
平行投影 中心投影
区别 物体与投影面平行时
联系 平行投影与中心投影的区别与联系
离点光源越近,影子越大;离点光源越远,影子越小
影子与物体全等
都是物体在光线的照射下在某个平面内形成的影子,即都是投影
2.举例说明生活中的中心投影现象.
解:路灯,手电筒照射物体时投影面出现影子.
1.下列各种现象属于中心投影现象的是( )
A.上午10点时,走在路上的人的影子
B.晚上10点时,走在路灯下的人的影子
C.中午用来乘凉的树影
D.升国旗时,地上旗杆的影子
B
随堂练习
3.两棵小树在一盏路灯下的影子如图所示.
(1)确定该路灯灯泡所在的位置;
(2)画出图中表示婷婷影长的线段.
解:(1)如图所示,点O就是路灯灯泡所在的位置.
(2)如图所示,表示婷婷影长的线段为CD.
A
B
C
D
O
随堂练习
随堂练习
4.如图,路边有一盏路灯.
长度相同的两根竹竿在这盏路灯下的影子一定一样长吗?如果不一定,那么什么情况下它们的影子一样长?
解:
不一定.
当它们到这盏路灯的距离一样时,它们的影子一样长.
解:如图,A为灯泡,EB为桌面半径,DC为桌面影子的半径.
∴AE=2.5,ED=1.2,EB=0.5.
∵EB∥DC,∴,
随堂练习
5.现有直径为1m的圆桌面,桌脚高1.2m(不计桌面厚度).如图所示,在桌面正上方2.5m处有一盏灯.你能测算出晚上开灯后圆桌面在地面上的影子的面积吗? (取π=3.14,精确到0.1m)
∴DC=·AD=(2.5+1.2)=0.74.
S影子=π×(0.74)2≈3.14×0.55≈1.7(m2).
∴圆桌面在地面上的影子的面积
是1.7 m2.
随堂练习
5.现有直径为1m的圆桌面,桌脚高1.2m(不计桌面厚度).如图所示,在桌面正上方2.5m处有一盏灯.你能测算出晚上开灯后圆桌面在地面上的影子的面积吗? (取π=3.14,精确到0.1m)
课堂小结
本节课学习了哪些内容?
1.中心投影的概念及特点.
2.中心投影的画法和计算.
3.平行投影和中心投影的区别与联系.
