2022-2023学年浙教版数学九年级下册3.4.1 直棱柱的表面展开图 课件 (共22张PPT)
文档属性
| 名称 | 2022-2023学年浙教版数学九年级下册3.4.1 直棱柱的表面展开图 课件 (共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-16 09:12:47 | ||
图片预览





文档简介
(共22张PPT)
3.4 简单几何体的表面展开图
第1课时 直棱柱的表面展开图
学习目标
通过展开、折叠,感受立体图形与平面图形的关系.
能想象并画出简单几何体的表面展开图,能根据表面展开图判断、制作简单几何体,并能进行相关计算.
经历和体验图形的变化过程,发展空间观念,养成研究性学习的良好习惯.
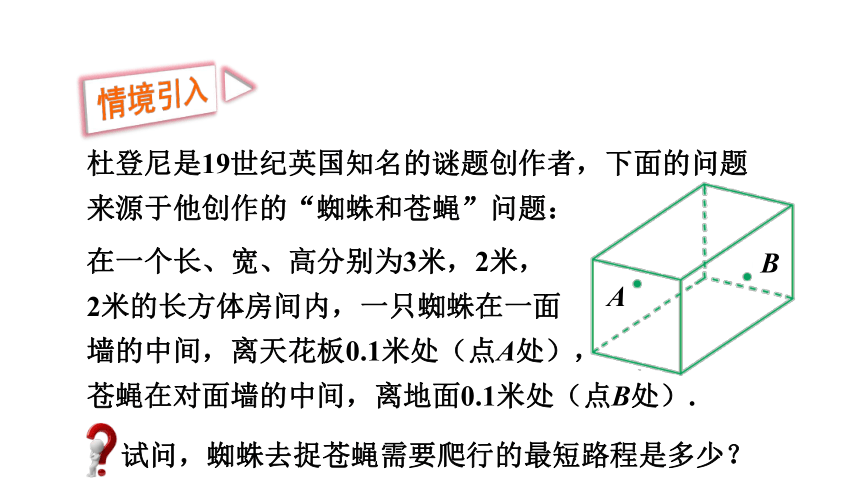
杜登尼是19世纪英国知名的谜题创作者,下面的问题来源于他创作的“蜘蛛和苍蝇”问题:
情境引入
在一个长、宽、高分别为3米,2米,
2米的长方体房间内,一只蜘蛛在一面
墙的中间,离天花板0.1米处(点A处),
苍蝇在对面墙的中间,离地面0.1米处(点B处).
试问,蜘蛛去捉苍蝇需要爬行的最短路程是多少?
A
B
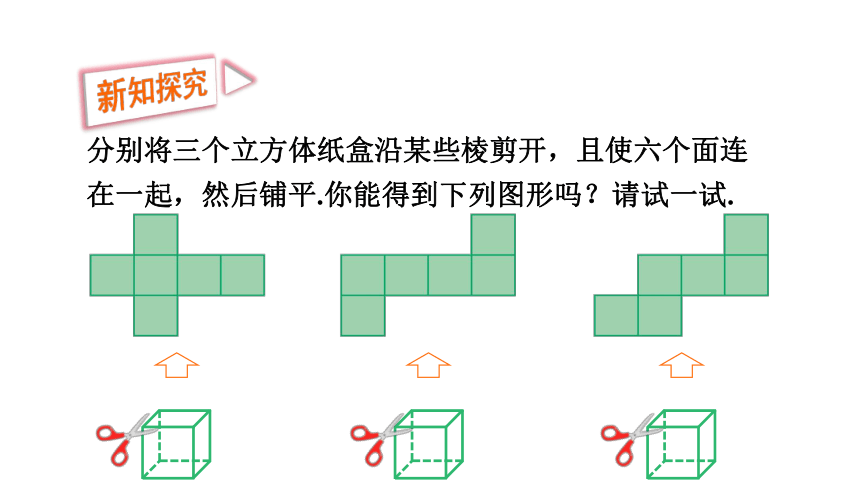
分别将三个立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平.你能得到下列图形吗?请试一试.
新知探究
将几何体沿着某些棱“剪开”,并使各个面连在一起,铺平所得到的平面图形称为几何体的表面展开图.
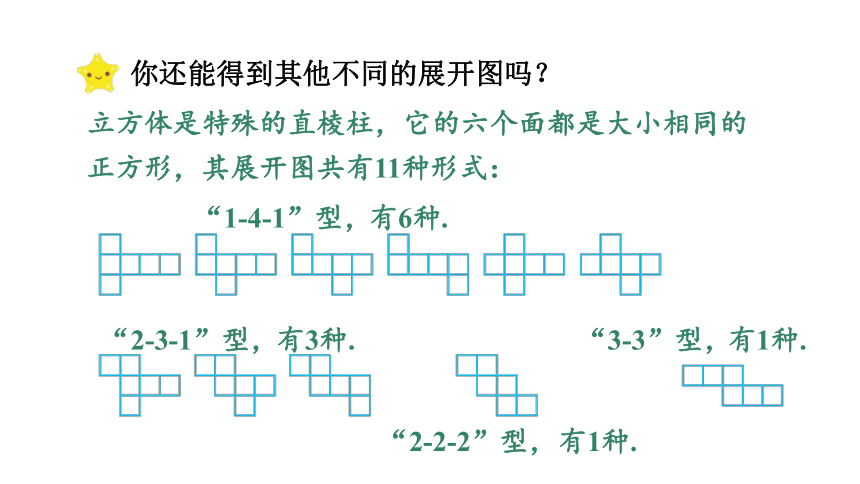
“1-4-1”型,
有6种.
“2-3-1”型,
有3种.
“2-2-2”型,
有1种.
“3-3”型,
有1种.
立方体是特殊的直棱柱,它的六个面都是大小相同的正方形,其展开图共有11种形式:
你还能得到其他不同的展开图吗?
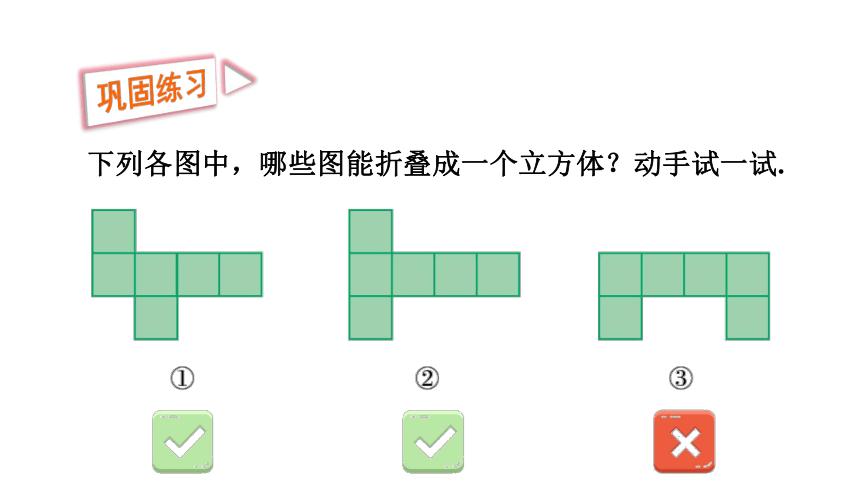
下列各图中,哪些图能折叠成一个立方体?动手试一试.
巩固练习
不管六个正方形如何排列,一旦某展开图出现“凹”字型或“田”字型,则该展开图一定不是立方体的展开图.
例1 如图是一个立方体的表面展开图吗?如果是,分别用1,2,3,4,5,6中的同一个数字表示立方体和它的展开图中各对对应的面(只要求给出一种表示法).
典例精讲
分析 可以先用折叠的方法试一试,看它能否折成一个立方体.
解 如图是一个立方体的表面展开图,
各对应面上的数字表示如图所示.
6
2
3
4
5
1
1
2
3
4
5
6
例1 如图是一个立方体的表面展开图吗?如果是,分别用1,2,3,4,5,6中的同一个数字表示立方体和它的展开图中各对对应的面(只要求给出一种表示法).
例2 如图,为了生产这种牛奶包装盒,需要
先画出展开图纸样.
(1)如图给出三种纸样,它们都正确吗?
甲
乙
丙
解 (1)右图中,因为表示底面的两个长方形不可能在同一侧,
所以图乙不正确.
图甲和图丙都正确.
例2 如图,为了生产这种牛奶包装盒,需要
先画出展开图纸样.
(2)从正确的纸样中选出一种,标注上尺寸.
(2)若选图甲,可得表面展开图及尺寸标注如图所示.
(3)由右图得,包装盒的侧面积和全面积为
S侧=(b+a+b+a)h=2ah+2bh;
S全=S侧+2S底=2ah+2bh+2ab.
例2 如图,为了生产这种牛奶包装盒,需要
先画出展开图纸样.
(3)利用你所选的一种纸样,求出包装盒的
侧面积和全面积(侧面积与两个底面积的和).
判断直棱柱表面展开图的策略
一般地,直棱柱的表面展开图由两个相同的多边形和一个大长方形(由多个小长方形组成)组成,两个多边形的边数与组成大长方形的小长方形的个数相同,且在大长方形的两侧.
直棱柱的侧面积和全面积
(1)侧面积:直棱柱的侧面积=直棱柱的底面周长×侧棱长(或直棱柱的高).
(2)全面积:S全=S侧十2S底.
在一个长、宽、高分别为3米,2米,
2米的长方体房间内,一只蜘蛛在一面墙的中间,离天花板0.1米处(点A处),苍蝇在对面墙的中间,离地面0.1米处(点B处).
试问,蜘蛛去捉苍蝇需要爬行的最短路程是多少?
试解决本课时“情境引入” 中的问题.
A
B
问题解决
解:把长方体展开后归纳可分4种
情况:
如图①,
AB=0.1+3+1.9=5(m);
如图②,
(m);
A
B
A
B
①
②
上底面
右侧面
左侧面
如图③,
(m);
如图④,
(m).
所以蜘蛛去捉苍蝇需要爬行的最短
路程是5米.
A
B
A
B
③
④
上底面
左侧面
上底面
下底面
“化折为直”求最短路径
确定直棱柱表面上两点之间的最短路径时,常需先把相关的面展开在同一平面内,通过“化折为直”,再根据“两点之间,线段最短”借助勾股定理求路程.此类问题在展开时的方式往往不唯一,故需全面考虑,通过比较各种情况下路程的长短来判断最短路径.
课堂小结
直棱柱的
表面展开图
表面展开图的概念
立方体的展开图
判断直棱柱表面展开图的策略
直棱柱的侧面积和全面积
“化折为直”求最短路径
1.下面哪些图形经过折叠可以围成一个棱柱?
当堂检测
2.画出如图所示的底面为正三角形的直棱柱的表面展开图(尺寸大小自选).
解:如图所示(答案不唯一).
3.4 简单几何体的表面展开图
第1课时 直棱柱的表面展开图
学习目标
通过展开、折叠,感受立体图形与平面图形的关系.
能想象并画出简单几何体的表面展开图,能根据表面展开图判断、制作简单几何体,并能进行相关计算.
经历和体验图形的变化过程,发展空间观念,养成研究性学习的良好习惯.
杜登尼是19世纪英国知名的谜题创作者,下面的问题来源于他创作的“蜘蛛和苍蝇”问题:
情境引入
在一个长、宽、高分别为3米,2米,
2米的长方体房间内,一只蜘蛛在一面
墙的中间,离天花板0.1米处(点A处),
苍蝇在对面墙的中间,离地面0.1米处(点B处).
试问,蜘蛛去捉苍蝇需要爬行的最短路程是多少?
A
B
分别将三个立方体纸盒沿某些棱剪开,且使六个面连在一起,然后铺平.你能得到下列图形吗?请试一试.
新知探究
将几何体沿着某些棱“剪开”,并使各个面连在一起,铺平所得到的平面图形称为几何体的表面展开图.
“1-4-1”型,
有6种.
“2-3-1”型,
有3种.
“2-2-2”型,
有1种.
“3-3”型,
有1种.
立方体是特殊的直棱柱,它的六个面都是大小相同的正方形,其展开图共有11种形式:
你还能得到其他不同的展开图吗?
下列各图中,哪些图能折叠成一个立方体?动手试一试.
巩固练习
不管六个正方形如何排列,一旦某展开图出现“凹”字型或“田”字型,则该展开图一定不是立方体的展开图.
例1 如图是一个立方体的表面展开图吗?如果是,分别用1,2,3,4,5,6中的同一个数字表示立方体和它的展开图中各对对应的面(只要求给出一种表示法).
典例精讲
分析 可以先用折叠的方法试一试,看它能否折成一个立方体.
解 如图是一个立方体的表面展开图,
各对应面上的数字表示如图所示.
6
2
3
4
5
1
1
2
3
4
5
6
例1 如图是一个立方体的表面展开图吗?如果是,分别用1,2,3,4,5,6中的同一个数字表示立方体和它的展开图中各对对应的面(只要求给出一种表示法).
例2 如图,为了生产这种牛奶包装盒,需要
先画出展开图纸样.
(1)如图给出三种纸样,它们都正确吗?
甲
乙
丙
解 (1)右图中,因为表示底面的两个长方形不可能在同一侧,
所以图乙不正确.
图甲和图丙都正确.
例2 如图,为了生产这种牛奶包装盒,需要
先画出展开图纸样.
(2)从正确的纸样中选出一种,标注上尺寸.
(2)若选图甲,可得表面展开图及尺寸标注如图所示.
(3)由右图得,包装盒的侧面积和全面积为
S侧=(b+a+b+a)h=2ah+2bh;
S全=S侧+2S底=2ah+2bh+2ab.
例2 如图,为了生产这种牛奶包装盒,需要
先画出展开图纸样.
(3)利用你所选的一种纸样,求出包装盒的
侧面积和全面积(侧面积与两个底面积的和).
判断直棱柱表面展开图的策略
一般地,直棱柱的表面展开图由两个相同的多边形和一个大长方形(由多个小长方形组成)组成,两个多边形的边数与组成大长方形的小长方形的个数相同,且在大长方形的两侧.
直棱柱的侧面积和全面积
(1)侧面积:直棱柱的侧面积=直棱柱的底面周长×侧棱长(或直棱柱的高).
(2)全面积:S全=S侧十2S底.
在一个长、宽、高分别为3米,2米,
2米的长方体房间内,一只蜘蛛在一面墙的中间,离天花板0.1米处(点A处),苍蝇在对面墙的中间,离地面0.1米处(点B处).
试问,蜘蛛去捉苍蝇需要爬行的最短路程是多少?
试解决本课时“情境引入” 中的问题.
A
B
问题解决
解:把长方体展开后归纳可分4种
情况:
如图①,
AB=0.1+3+1.9=5(m);
如图②,
(m);
A
B
A
B
①
②
上底面
右侧面
左侧面
如图③,
(m);
如图④,
(m).
所以蜘蛛去捉苍蝇需要爬行的最短
路程是5米.
A
B
A
B
③
④
上底面
左侧面
上底面
下底面
“化折为直”求最短路径
确定直棱柱表面上两点之间的最短路径时,常需先把相关的面展开在同一平面内,通过“化折为直”,再根据“两点之间,线段最短”借助勾股定理求路程.此类问题在展开时的方式往往不唯一,故需全面考虑,通过比较各种情况下路程的长短来判断最短路径.
课堂小结
直棱柱的
表面展开图
表面展开图的概念
立方体的展开图
判断直棱柱表面展开图的策略
直棱柱的侧面积和全面积
“化折为直”求最短路径
1.下面哪些图形经过折叠可以围成一个棱柱?
当堂检测
2.画出如图所示的底面为正三角形的直棱柱的表面展开图(尺寸大小自选).
解:如图所示(答案不唯一).
