2.1一元二次方程 课件(共23张PPT)
文档属性
| 名称 | 2.1一元二次方程 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 861.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-19 08:20:49 | ||
图片预览






文档简介
(共23张PPT)
浙教版八下数学
第二章 一元二次方程
2.1 一元二次方程
重要的,整理+综上联立
数学的本质是在认识数的同时,认识数量之间的关系(多与少),进一步抽象,是数与数之间的关系(大与小)。
两个相关联的数或数量之间的关系,初中阶段主要可分为三类:一是加减运算的和差关系,二是乘除运算的倍比关系,三是乘方、开方运算的幂、方根关系。
百分数属于倍比关系,表示一个数是另一个数的百分之几的数。
增长率:增加的数额与原来的数额的比例关系,用“%”表示。
温故知新:
列出下列问题中关于未知数x的方程:
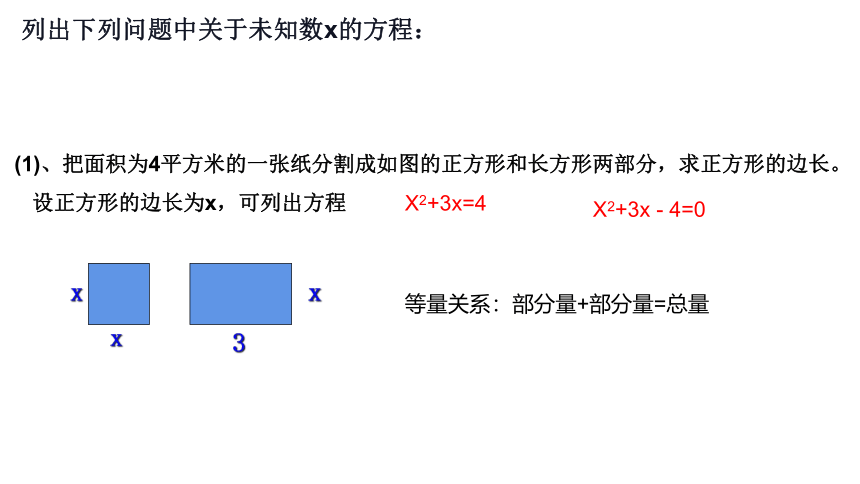
(1)、把面积为4平方米的一张纸分割成如图的正方形和长方形两部分,求正方形的边长。
设正方形的边长为x,可列出方程
x
x
x
3
X2+3x=4
等量关系:部分量+部分量=总量
X2+3x - 4=0
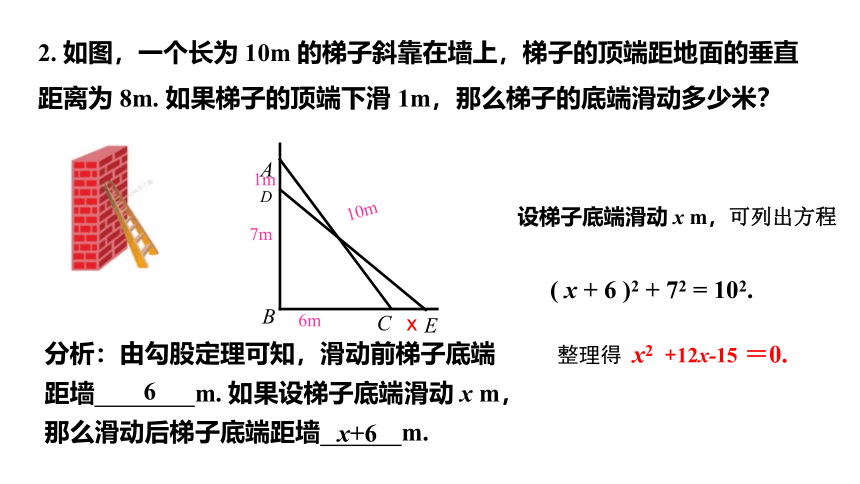
2. 如图,一个长为 10m 的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为 8m. 如果梯子的顶端下滑 1m,那么梯子的底端滑动多少米?
分析:由勾股定理可知,滑动前梯子底端距墙 m. 如果设梯子底端滑动 x m,那么滑动后梯子底端距墙 m.
6
x+6
( x + 6 )2 + 72 = 102.
设梯子底端滑动 x m,可列出方程
整理得 x2 +12x-15 =0.
7m
C
1m
10m
A
B
D
E
6m
x
3.学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册.求这两年的年平均增长率.
可列得方程5(1+x)2=7.2,
分析:
设这两年的年平均增长率为x,
去年年底的图书数是5万册,
则今年年底的图书数是5(1+x)万册;
同样,明年年底的图书数又是今年年底的(1+x)倍,
即5(1+x)(1+x)=5(1+x)2万册.
总结:原来的量,变化后的量,平均增长率以及变化的次数之间的关系
a S x% n
5x2 +10x-2.2=0.
4.要组织一次排球邀请赛,参赛的每两队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参加比赛
分析:
全部比赛共
4×7=28场.
设应邀请x个队参赛,每个队要与其他 个队各赛1场,
(x-1)
由于甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛,所以全部比赛共 场.
x2-x=56
.
x2-x-56=0
像这样,两边都是整式,只含有一个未知数且未知数的最高次数是2次的方程叫做一元二次方程.
x2 +12x-15 =0.
x2-x-56=0
5x2 +10x-2.2=0.
判断下列方程是否为一元二次方程:
① 10x2=9 ( ) ②2(x-1)=3x ( )
③2x2-3x-1=0 ( ) ④ =0 ( )
学以致用:
X2+3x- 4=0
√
×
√
×
能使一元二次方程两边相等的未知数的值叫一元二次方程的解(或根).
.判断未知数的值x= -1,x=0,x=2是不是方程x2-2=x的根.
练习:
当x=2时,左边=2 -2=4-2=2
右边=2
因为:左边=右边
所以x=2是方程的解。
解:当x=-1时,
左边=(-1) -2=1-2=-1
右边=-1
因为:左边=右边
所以x=-1是方程的解。
当x=0时,左边=0 -2=-2
右边=0
因为:左边≠ 右边
所以x=0不是方程的解。
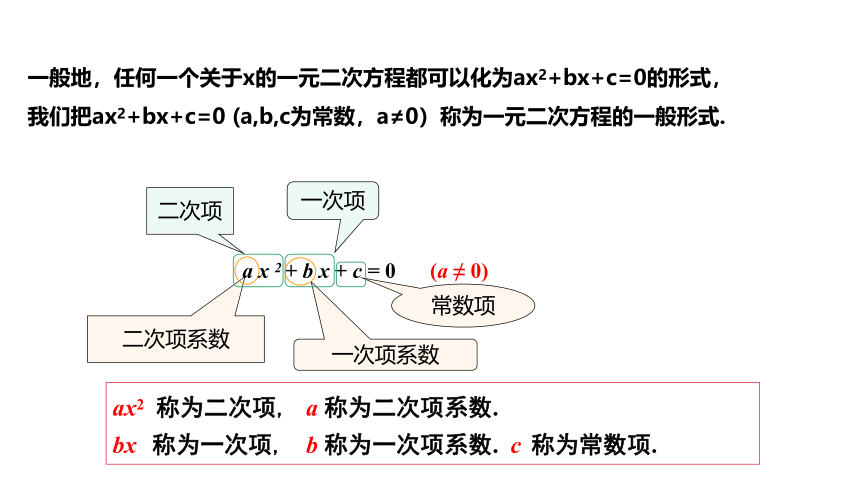
ax2 称为二次项, a 称为二次项系数.
bx 称为一次项, b 称为一次项系数. c 称为常数项.
a x 2 + b x + c = 0
(a ≠ 0)
二次项系数
一次项系数
常数项
二次项
一次项
一般地,任何一个关于x的一元二次方程都可以化为ax2+bx+c=0的形式,我们把ax2+bx+c=0 (a,b,c为常数,a≠0)称为一元二次方程的一般形式.
例1 把下列方程化成一元二次方程的一般形式,并写出它的二次项系数、
一次项系数和常数项.
(1)9x2=5-4x; (2)(2-x)(3x+4)=3.
解:(1)移项,整理得9x2+4x-5=0
这个方程的二次项系数是9,一次项系数是4,常数项是-5。
(2)方程左边多项式相乘,得-3x2+2x+8=3,
移项,整理得-3x2+2x+5=0
a=-3,b=2,c=5。
方程 一般形式 二次项系数 一次项系数 常数项
2x2-x=4
y-4y2=0
(2x)2=(x+1)2
2x2-x-4=0
3x2-2x-1=0
2
-1
-4
3 -2 -1
填表:
练习:
-4y2+ y=0
.
-4 0
.
解得
b=1
c=-15
所以这个一元二次方程是2x2+x-15=0
例2 已知一元二次方程 2x2+bx+c=0的两个根分别为x1= 和x2=-3,求这个方程.
.
解:将x1= 和x2=-3带入方程 2x2+bx+c=0得
2×()2+b+c=0
2×(-3)2+(-3)b+c=0
.
.
.
把x=3代入方程得:9+3a+a=0
练习:.已知关于x的一元二次方程 的一个根是3,求a的值,
x2+ax+a=0
a= -
.
一元二次方程
概念
是整式方程;
含一个未知数;
最高次数是2.
一般形式
ax2+bx+c=0 (a ≠0)
其中(a≠0)是一元二次方程的必要条件;
确定一元二次方程的二次项系数、一次项系数及常数项要先化为一般式.
根
使方程左右两边相等的未知数的值.
课堂小结
1.关于 x 的方程 (k-3)x2 + 2x-1=0,
当k 时,是一元二次方程.
≠3
2.关于 x 的方程(k2-1)x2 + 2 (k-1) x + 2k + 2=0,
当k 时,是一元二次方程.,
当k 时,是一元一次方程.
≠±1
=-1
夯实基础,稳扎稳打
.
且
.
同时满足
a=5,b=-4,c=-4.
系数和项均包含前面的符号.
3. 将一元二次方程(x-)(x+)+(2x-1)2=0化为一般形式,并写出其中的二次项系数、一次项系数、常数项.
.
解:(x2-5)+(4x2-4x+1)=0
x2-5+4x2-4x+1=0
5x2-4x-4=0
4. 关于x的一元二次方程(a+1)x2-ax+|a|-1=0的一个根为0,求a的值.
解:将x=0代入方程|a|-1=0,
解得a= ±1.
∵ a+1 ≠0,
∴ a ≠-1,
综上所述:a =1.
且
同时满足
.
.
解:由题意,得|m|=2,且m+2≠0,解得m=2.
∴当m=2时,(m+2)x|m|+2x-1=0是一元二次方程.
m≥0且m≠1
5.已知关于x的方程 . , 当m为何值时,该方程是一元二次方程?
.
.
.
m=2
.
被开方数
二次项系数
6.若方程(m-1)x2+ x=1是关于 x 的一元二次方程,求m的取值范围.
.
连续递推,豁然开朗
指数
(m+2)x+2x-1=0
.
7. 已知关于x的一元二次方程 ax2+bx+c=0 (a≠0)一个根为1, 求a+b+c的值.
解:由题意得
变形: 若 a+b+c=0,你能通过观察,求出方程ax2+bx+c=0 (a≠0)一个根吗
解:由题意得
方程ax2+bx+c=0 (a≠0)一个根是1.
推广: 若 a-b +c=0, 你能通过观察,求出方程ax2+bx+c=0 (a≠0)一个根吗
a+b+c=0
a+b+c=0
a+b
.
a+b
.
a+b
.
8.对于一元二次方程 ax2+bx+c=0 (a≠0),若a+b+c=0,则方程必有一个根为_______.
对于一元二次方程 ax2+bx+c=0 (a≠0),若a+c=b,则方程必有一个根为_______.
对于一元二次方程 ax2+bx+c=0 (a≠0),若4a+2b+c=0,则方程必有一个根为_______.
X=1
X=2
X= -1
对于一元二次方程 ax2+bx+c=0 (a≠0),若a-2b+4c=0,则方程必有一个根为_______.
x= -
.
9. 如图,一个长为 10m 的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为 8m. 如果梯子的顶端下滑 1m,那么梯子的底端滑动多少米?
分析:由勾股定理可知,滑动前梯子底端距墙 m. 如果设梯子底端滑动 x m,那么滑动后梯子底端距墙 m.
6
x+6
( x + 6 )2 + 72 = 102.
设梯子底端滑动 x m,可列出方程
整理得 x2 +12x-15 =0.
7m
C
1m
10m
A
B
D
E
6m
x
思维拓展,更上一层
梯子底端滑动的距离 x (m) 满足方程 ( x + 6 )2 + 72 = 102,
也就是 x2 + 12x - 15 = 0.
(1) 小明认为底端也滑动了 1m,他的说法正确吗?为什么?
(2) 底端滑动的距离可能是 2m 吗?可能是 3m 吗?为什么?
不正确,1 + 12 - 15 = -2.
距离是 2m 不可能,4 + 24 - 15 = 13.
距离是 3m 不满足方程,不是方程的解
小亮把他的求解过程整理如下:
x 0 0.5 1 1.5 2
x2 + 12 x - 15 -15 -8.75 -2 5.25 13
所以 1 < x <1.5,
进一步计算:
x 1.1 1.2 1.3 1.4
x2 + 12 x - 15 -0.59 0.84 2.29 3.76
所以 1.1 < x <1.2 .
浙教版八下数学
第二章 一元二次方程
2.1 一元二次方程
重要的,整理+综上联立
数学的本质是在认识数的同时,认识数量之间的关系(多与少),进一步抽象,是数与数之间的关系(大与小)。
两个相关联的数或数量之间的关系,初中阶段主要可分为三类:一是加减运算的和差关系,二是乘除运算的倍比关系,三是乘方、开方运算的幂、方根关系。
百分数属于倍比关系,表示一个数是另一个数的百分之几的数。
增长率:增加的数额与原来的数额的比例关系,用“%”表示。
温故知新:
列出下列问题中关于未知数x的方程:
(1)、把面积为4平方米的一张纸分割成如图的正方形和长方形两部分,求正方形的边长。
设正方形的边长为x,可列出方程
x
x
x
3
X2+3x=4
等量关系:部分量+部分量=总量
X2+3x - 4=0
2. 如图,一个长为 10m 的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为 8m. 如果梯子的顶端下滑 1m,那么梯子的底端滑动多少米?
分析:由勾股定理可知,滑动前梯子底端距墙 m. 如果设梯子底端滑动 x m,那么滑动后梯子底端距墙 m.
6
x+6
( x + 6 )2 + 72 = 102.
设梯子底端滑动 x m,可列出方程
整理得 x2 +12x-15 =0.
7m
C
1m
10m
A
B
D
E
6m
x
3.学校图书馆去年年底有图书5万册,预计到明年年底增加到7.2万册.求这两年的年平均增长率.
可列得方程5(1+x)2=7.2,
分析:
设这两年的年平均增长率为x,
去年年底的图书数是5万册,
则今年年底的图书数是5(1+x)万册;
同样,明年年底的图书数又是今年年底的(1+x)倍,
即5(1+x)(1+x)=5(1+x)2万册.
总结:原来的量,变化后的量,平均增长率以及变化的次数之间的关系
a S x% n
5x2 +10x-2.2=0.
4.要组织一次排球邀请赛,参赛的每两队之间都要比赛一场,根据场地和时间等条件,赛程计划安排7天,每天安排4场比赛,比赛组织者应邀请多少个队参加比赛
分析:
全部比赛共
4×7=28场.
设应邀请x个队参赛,每个队要与其他 个队各赛1场,
(x-1)
由于甲队对乙队的比赛和乙队对甲队的比赛是同一场比赛,所以全部比赛共 场.
x2-x=56
.
x2-x-56=0
像这样,两边都是整式,只含有一个未知数且未知数的最高次数是2次的方程叫做一元二次方程.
x2 +12x-15 =0.
x2-x-56=0
5x2 +10x-2.2=0.
判断下列方程是否为一元二次方程:
① 10x2=9 ( ) ②2(x-1)=3x ( )
③2x2-3x-1=0 ( ) ④ =0 ( )
学以致用:
X2+3x- 4=0
√
×
√
×
能使一元二次方程两边相等的未知数的值叫一元二次方程的解(或根).
.判断未知数的值x= -1,x=0,x=2是不是方程x2-2=x的根.
练习:
当x=2时,左边=2 -2=4-2=2
右边=2
因为:左边=右边
所以x=2是方程的解。
解:当x=-1时,
左边=(-1) -2=1-2=-1
右边=-1
因为:左边=右边
所以x=-1是方程的解。
当x=0时,左边=0 -2=-2
右边=0
因为:左边≠ 右边
所以x=0不是方程的解。
ax2 称为二次项, a 称为二次项系数.
bx 称为一次项, b 称为一次项系数. c 称为常数项.
a x 2 + b x + c = 0
(a ≠ 0)
二次项系数
一次项系数
常数项
二次项
一次项
一般地,任何一个关于x的一元二次方程都可以化为ax2+bx+c=0的形式,我们把ax2+bx+c=0 (a,b,c为常数,a≠0)称为一元二次方程的一般形式.
例1 把下列方程化成一元二次方程的一般形式,并写出它的二次项系数、
一次项系数和常数项.
(1)9x2=5-4x; (2)(2-x)(3x+4)=3.
解:(1)移项,整理得9x2+4x-5=0
这个方程的二次项系数是9,一次项系数是4,常数项是-5。
(2)方程左边多项式相乘,得-3x2+2x+8=3,
移项,整理得-3x2+2x+5=0
a=-3,b=2,c=5。
方程 一般形式 二次项系数 一次项系数 常数项
2x2-x=4
y-4y2=0
(2x)2=(x+1)2
2x2-x-4=0
3x2-2x-1=0
2
-1
-4
3 -2 -1
填表:
练习:
-4y2+ y=0
.
-4 0
.
解得
b=1
c=-15
所以这个一元二次方程是2x2+x-15=0
例2 已知一元二次方程 2x2+bx+c=0的两个根分别为x1= 和x2=-3,求这个方程.
.
解:将x1= 和x2=-3带入方程 2x2+bx+c=0得
2×()2+b+c=0
2×(-3)2+(-3)b+c=0
.
.
.
把x=3代入方程得:9+3a+a=0
练习:.已知关于x的一元二次方程 的一个根是3,求a的值,
x2+ax+a=0
a= -
.
一元二次方程
概念
是整式方程;
含一个未知数;
最高次数是2.
一般形式
ax2+bx+c=0 (a ≠0)
其中(a≠0)是一元二次方程的必要条件;
确定一元二次方程的二次项系数、一次项系数及常数项要先化为一般式.
根
使方程左右两边相等的未知数的值.
课堂小结
1.关于 x 的方程 (k-3)x2 + 2x-1=0,
当k 时,是一元二次方程.
≠3
2.关于 x 的方程(k2-1)x2 + 2 (k-1) x + 2k + 2=0,
当k 时,是一元二次方程.,
当k 时,是一元一次方程.
≠±1
=-1
夯实基础,稳扎稳打
.
且
.
同时满足
a=5,b=-4,c=-4.
系数和项均包含前面的符号.
3. 将一元二次方程(x-)(x+)+(2x-1)2=0化为一般形式,并写出其中的二次项系数、一次项系数、常数项.
.
解:(x2-5)+(4x2-4x+1)=0
x2-5+4x2-4x+1=0
5x2-4x-4=0
4. 关于x的一元二次方程(a+1)x2-ax+|a|-1=0的一个根为0,求a的值.
解:将x=0代入方程|a|-1=0,
解得a= ±1.
∵ a+1 ≠0,
∴ a ≠-1,
综上所述:a =1.
且
同时满足
.
.
解:由题意,得|m|=2,且m+2≠0,解得m=2.
∴当m=2时,(m+2)x|m|+2x-1=0是一元二次方程.
m≥0且m≠1
5.已知关于x的方程 . , 当m为何值时,该方程是一元二次方程?
.
.
.
m=2
.
被开方数
二次项系数
6.若方程(m-1)x2+ x=1是关于 x 的一元二次方程,求m的取值范围.
.
连续递推,豁然开朗
指数
(m+2)x+2x-1=0
.
7. 已知关于x的一元二次方程 ax2+bx+c=0 (a≠0)一个根为1, 求a+b+c的值.
解:由题意得
变形: 若 a+b+c=0,你能通过观察,求出方程ax2+bx+c=0 (a≠0)一个根吗
解:由题意得
方程ax2+bx+c=0 (a≠0)一个根是1.
推广: 若 a-b +c=0, 你能通过观察,求出方程ax2+bx+c=0 (a≠0)一个根吗
a+b+c=0
a+b+c=0
a+b
.
a+b
.
a+b
.
8.对于一元二次方程 ax2+bx+c=0 (a≠0),若a+b+c=0,则方程必有一个根为_______.
对于一元二次方程 ax2+bx+c=0 (a≠0),若a+c=b,则方程必有一个根为_______.
对于一元二次方程 ax2+bx+c=0 (a≠0),若4a+2b+c=0,则方程必有一个根为_______.
X=1
X=2
X= -1
对于一元二次方程 ax2+bx+c=0 (a≠0),若a-2b+4c=0,则方程必有一个根为_______.
x= -
.
9. 如图,一个长为 10m 的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为 8m. 如果梯子的顶端下滑 1m,那么梯子的底端滑动多少米?
分析:由勾股定理可知,滑动前梯子底端距墙 m. 如果设梯子底端滑动 x m,那么滑动后梯子底端距墙 m.
6
x+6
( x + 6 )2 + 72 = 102.
设梯子底端滑动 x m,可列出方程
整理得 x2 +12x-15 =0.
7m
C
1m
10m
A
B
D
E
6m
x
思维拓展,更上一层
梯子底端滑动的距离 x (m) 满足方程 ( x + 6 )2 + 72 = 102,
也就是 x2 + 12x - 15 = 0.
(1) 小明认为底端也滑动了 1m,他的说法正确吗?为什么?
(2) 底端滑动的距离可能是 2m 吗?可能是 3m 吗?为什么?
不正确,1 + 12 - 15 = -2.
距离是 2m 不可能,4 + 24 - 15 = 13.
距离是 3m 不满足方程,不是方程的解
小亮把他的求解过程整理如下:
x 0 0.5 1 1.5 2
x2 + 12 x - 15 -15 -8.75 -2 5.25 13
所以 1 < x <1.5,
进一步计算:
x 1.1 1.2 1.3 1.4
x2 + 12 x - 15 -0.59 0.84 2.29 3.76
所以 1.1 < x <1.2 .
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
