第二章 直线与圆的位置关系 单元测试(含答案)
文档属性
| 名称 | 第二章 直线与圆的位置关系 单元测试(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 326.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-19 18:18:23 | ||
图片预览

文档简介
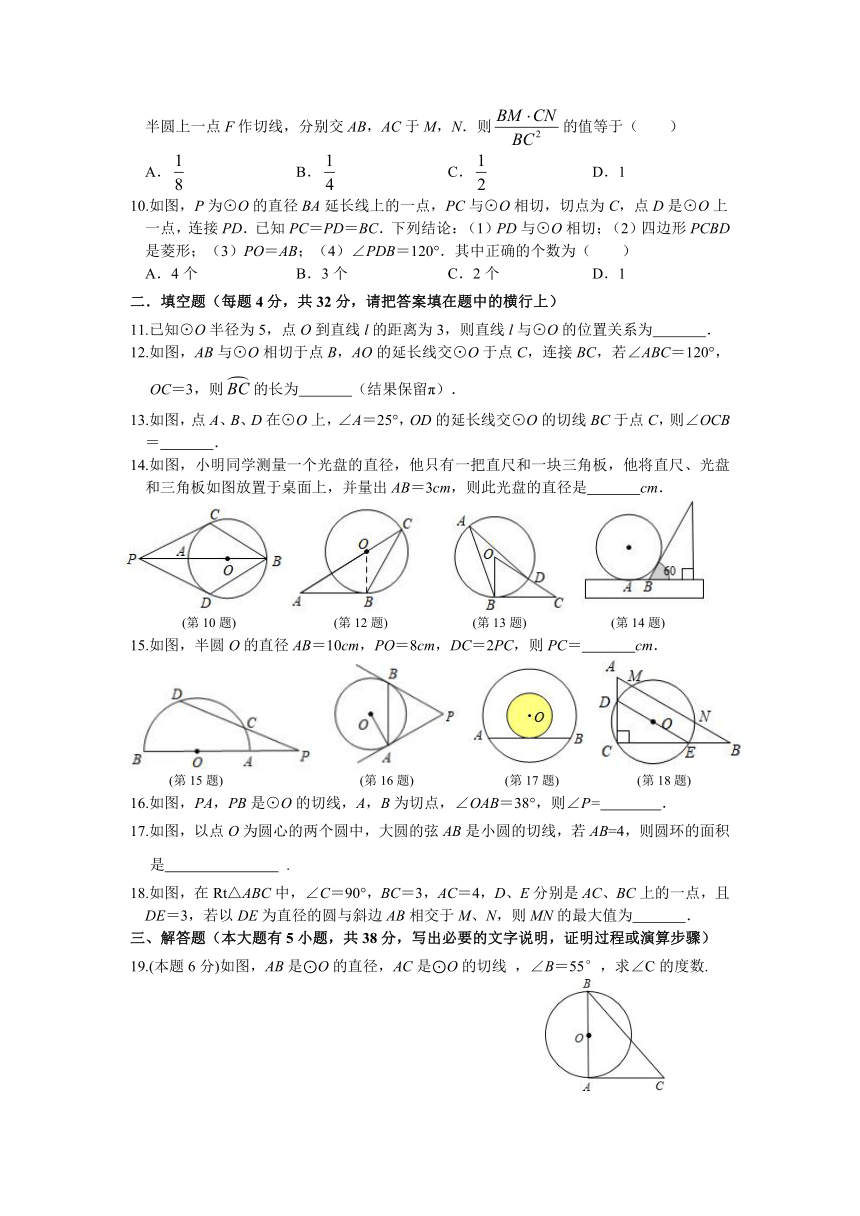
第2章《直线与圆的位置关系》单元练习卷(HJQ)
班级__________姓名__________学号__________成绩__________
一、选择题(本大题共10小题,每小题3分,共30分,每小题有且只有一个正确答案)
1.已知⊙O的半径为3,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
2.平面内,⊙O的半径为1,点P到圆心O的距离为2,过点P可作⊙O的切线条数为( )
A.0条 B.1条 C.2条 D.无数条
3.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条高的交点
(第3题) (第4题) (第5题) (第6题)
4.如图,PA、PB切⊙O于点A、B,PA=4,CD切⊙O于点E,交PA、PB于C、D两点,
...则△PCD的周长是( )
A.4 B.8 C.12 D.16
5.如图,P为⊙O外一点,PA切⊙O于点A,⊙O的半径为6,且PA=8,则cos∠P等于( ).
A. B. C. D.
6.如图,两个同心圆(圆心相同、半径不同的圆)的半径分别为6 cm和3 cm,大圆的弦AB
.与小圆相切,则劣弧的长为( )
A.2π cm B.4π cm C.6π cm D.8π cm
7.如图,已知AB、AC分别为⊙O的直径和弦,D为的中点,DE垂直于AC,交AC的延长线于E,连接BC,若DE=6cm,CE=2cm,则下列结论:①DE是⊙O的切线;②直径AB长为20cm;③弦AC长为15cm;④C为的中点,其中正确的是( )
A.①②④ B.①③④ C.①② D.②③
8.如图,AB为⊙O的直径,C、D为⊙O上的点,直线MN切⊙O于C点,图中与∠BCN
...互余的角有( )
A.1个 B.2个 C.3个 D.4个
(第7题) (第8题) (第9题)
9.如图,在等腰△ABC中,O为底边BC的中点,以O为圆心作半圆与AB,AC相切,过
半圆上一点F作切线,分别交AB,AC于M,N.则的值等于( )
A. B. C. D.1
10.如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.其中正确的个数为( )
A.4个 B.3个 C.2个 D.1
二.填空题(每题4分,共32分,请把答案填在题中的横行上)
11.已知⊙O半径为5,点O到直线l的距离为3,则直线l与⊙O的位置关系为 .
12.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则的长为 (结果保留π).
13.如图,点A、B、D在⊙O上,∠A=25°,OD的延长线交⊙O的切线BC于点C,则∠OCB= .
14.如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的直径是 cm.
(第10题) (第12题) (第13题) (第14题)
15.如图,半圆O的直径AB=10cm,PO=8cm,DC=2PC,则PC= cm.
(第15题) (第16题) (第17题) (第18题)
16.如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P= .
17.如图,以点O为圆心的两个圆中,大圆的弦AB是小圆的切线,若AB=4,则圆环的面积是 .
18.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3,若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为 .
三、解答题(本大题有5小题,共38分,写出必要的文字说明,证明过程或演算步骤)
19.(本题6分)如图,AB是⊙O的直径,AC是⊙O的切线 ,∠B=55°,求∠C的度数.
20.(本题6分)如图,在矩形ABCD中,AB=3,BC=4,P是对角线BD上的动点,以BP为直径作圆,当圆与矩形ABCD的边相切时,求BP的长.
21.(本题6分)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,且AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为2,求图中阴影部分的面积.
22.(本题10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,垂足为点E.
(1)求证:△ABD≌△ACD;
(2)判断直线DE与⊙O的位置关系,并说明理由.
23.(本题10分)如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
(1)求证:∠ECD=∠EDC;
(2)若tanA=,求DE长;
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.
第2章《直线与圆的位置关系》单元练习卷
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B B A B C C B A
填空题:11.相交;12.;13.40°;14.;15.;16.76°;17.;18.12/5;
三、19---22(答案略)解答题:23.(1)证明:连结OD,∵DE是⊙O切线,∴∠EDC+∠ODA=900, 又∵OA⊥OB,∴∠ACO+∠A=900, ∵OA=OD,∴∠ODA=∠A,∴∠EDC=∠ACO, 又∵∠ECD=∠ACO,∴∠ECD=∠EDC.
(2)解:∵tanA=,∴,∴OC=2, 设DE=x,∵∠ECD=∠EDC,
∴CE=x,∴OE=2+x.∴∠ODE=900,∴OD2+DE2=OE2,
∴82+x 2=(2+x)2,x=15,∴DE=CE=15.
解:过点D作AO的垂线,交AO的延长于F,
当时,,DF=4, 当时,,DF=4,,
班级__________姓名__________学号__________成绩__________
一、选择题(本大题共10小题,每小题3分,共30分,每小题有且只有一个正确答案)
1.已知⊙O的半径为3,圆心O到直线l的距离为2,则直线l与⊙O的位置关系是( )
A.相交 B.相切 C.相离 D.不能确定
2.平面内,⊙O的半径为1,点P到圆心O的距离为2,过点P可作⊙O的切线条数为( )
A.0条 B.1条 C.2条 D.无数条
3.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )
A.三条边的垂直平分线的交点 B.三条角平分线的交点
C.三条中线的交点 D.三条高的交点
(第3题) (第4题) (第5题) (第6题)
4.如图,PA、PB切⊙O于点A、B,PA=4,CD切⊙O于点E,交PA、PB于C、D两点,
...则△PCD的周长是( )
A.4 B.8 C.12 D.16
5.如图,P为⊙O外一点,PA切⊙O于点A,⊙O的半径为6,且PA=8,则cos∠P等于( ).
A. B. C. D.
6.如图,两个同心圆(圆心相同、半径不同的圆)的半径分别为6 cm和3 cm,大圆的弦AB
.与小圆相切,则劣弧的长为( )
A.2π cm B.4π cm C.6π cm D.8π cm
7.如图,已知AB、AC分别为⊙O的直径和弦,D为的中点,DE垂直于AC,交AC的延长线于E,连接BC,若DE=6cm,CE=2cm,则下列结论:①DE是⊙O的切线;②直径AB长为20cm;③弦AC长为15cm;④C为的中点,其中正确的是( )
A.①②④ B.①③④ C.①② D.②③
8.如图,AB为⊙O的直径,C、D为⊙O上的点,直线MN切⊙O于C点,图中与∠BCN
...互余的角有( )
A.1个 B.2个 C.3个 D.4个
(第7题) (第8题) (第9题)
9.如图,在等腰△ABC中,O为底边BC的中点,以O为圆心作半圆与AB,AC相切,过
半圆上一点F作切线,分别交AB,AC于M,N.则的值等于( )
A. B. C. D.1
10.如图,P为⊙O的直径BA延长线上的一点,PC与⊙O相切,切点为C,点D是⊙O上一点,连接PD.已知PC=PD=BC.下列结论:(1)PD与⊙O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)∠PDB=120°.其中正确的个数为( )
A.4个 B.3个 C.2个 D.1
二.填空题(每题4分,共32分,请把答案填在题中的横行上)
11.已知⊙O半径为5,点O到直线l的距离为3,则直线l与⊙O的位置关系为 .
12.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则的长为 (结果保留π).
13.如图,点A、B、D在⊙O上,∠A=25°,OD的延长线交⊙O的切线BC于点C,则∠OCB= .
14.如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的直径是 cm.
(第10题) (第12题) (第13题) (第14题)
15.如图,半圆O的直径AB=10cm,PO=8cm,DC=2PC,则PC= cm.
(第15题) (第16题) (第17题) (第18题)
16.如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P= .
17.如图,以点O为圆心的两个圆中,大圆的弦AB是小圆的切线,若AB=4,则圆环的面积是 .
18.如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3,若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为 .
三、解答题(本大题有5小题,共38分,写出必要的文字说明,证明过程或演算步骤)
19.(本题6分)如图,AB是⊙O的直径,AC是⊙O的切线 ,∠B=55°,求∠C的度数.
20.(本题6分)如图,在矩形ABCD中,AB=3,BC=4,P是对角线BD上的动点,以BP为直径作圆,当圆与矩形ABCD的边相切时,求BP的长.
21.(本题6分)如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,且AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为2,求图中阴影部分的面积.
22.(本题10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC,垂足为点E.
(1)求证:△ABD≌△ACD;
(2)判断直线DE与⊙O的位置关系,并说明理由.
23.(本题10分)如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
(1)求证:∠ECD=∠EDC;
(2)若tanA=,求DE长;
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.
第2章《直线与圆的位置关系》单元练习卷
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B B A B C C B A
填空题:11.相交;12.;13.40°;14.;15.;16.76°;17.;18.12/5;
三、19---22(答案略)解答题:23.(1)证明:连结OD,∵DE是⊙O切线,∴∠EDC+∠ODA=900, 又∵OA⊥OB,∴∠ACO+∠A=900, ∵OA=OD,∴∠ODA=∠A,∴∠EDC=∠ACO, 又∵∠ECD=∠ACO,∴∠ECD=∠EDC.
(2)解:∵tanA=,∴,∴OC=2, 设DE=x,∵∠ECD=∠EDC,
∴CE=x,∴OE=2+x.∴∠ODE=900,∴OD2+DE2=OE2,
∴82+x 2=(2+x)2,x=15,∴DE=CE=15.
解:过点D作AO的垂线,交AO的延长于F,
当时,,DF=4, 当时,,DF=4,,
