浙教版八年级数学下册 2.3 一元二次方程的应用 教案(表格式)
文档属性
| 名称 | 浙教版八年级数学下册 2.3 一元二次方程的应用 教案(表格式) |
|
|
| 格式 | doc | ||
| 文件大小 | 45.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-19 00:00:00 | ||
图片预览

文档简介
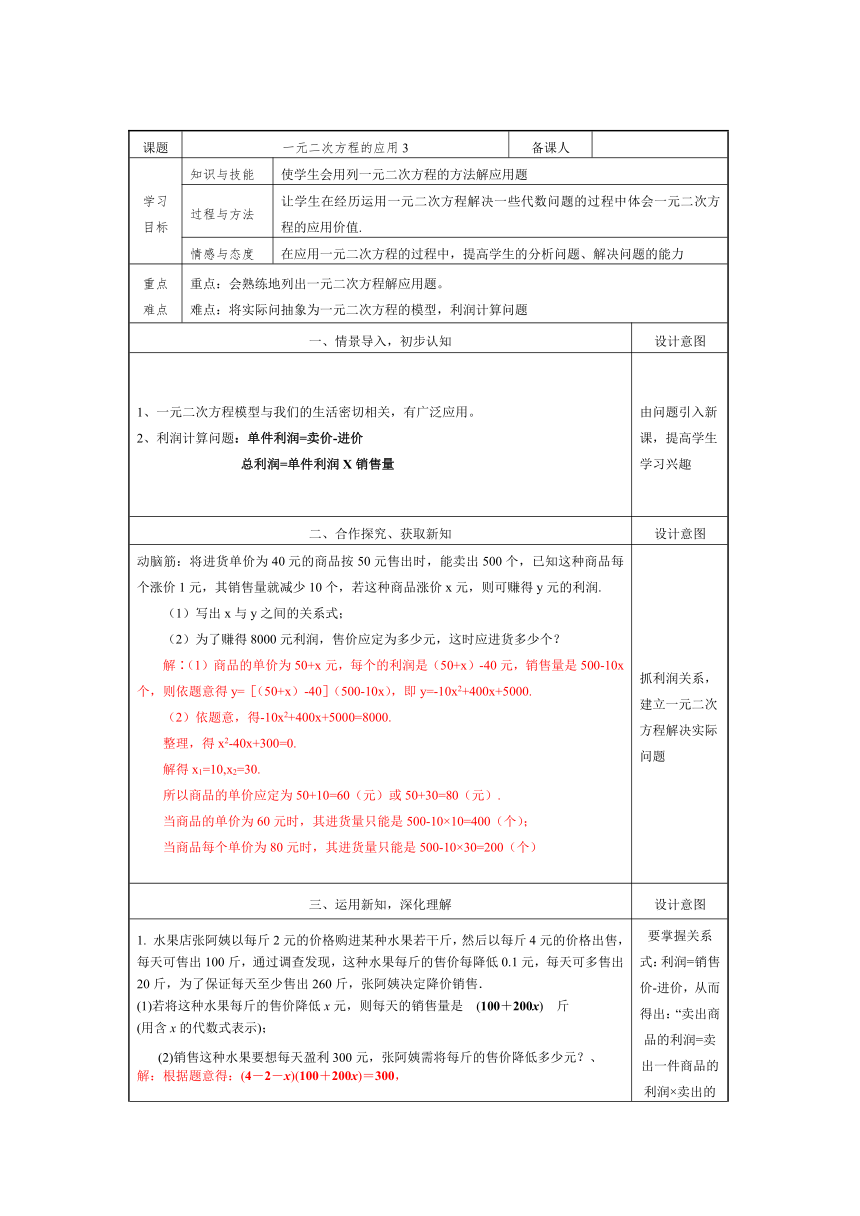
课题 一元二次方程的应用3 备课人
学习目标 知识与技能 使学生会用列一元二次方程的方法解应用题
过程与方法 让学生在经历运用一元二次方程解决一些代数问题的过程中体会一元二次方程的应用价值.
情感与态度 在应用一元二次方程的过程中,提高学生的分析问题、解决问题的能力
重点难点 重点:会熟练地列出一元二次方程解应用题。难点:将实际问抽象为一元二次方程的模型,利润计算问题
一、情景导入,初步认知 设计意图
1、一元二次方程模型与我们的生活密切相关,有广泛应用。2、利润计算问题:单件利润=卖价-进价 总利润=单件利润X销售量 由问题引入新课,提高学生学习兴趣
二、合作探究、获取新知 设计意图
动脑筋:将进货单价为40元的商品按50元售出时,能卖出500个,已知这种商品每个涨价1元,其销售量就减少10个,若这种商品涨价x元,则可赚得y元的利润.(1)写出x与y之间的关系式;(2)为了赚得8000元利润,售价应定为多少元,这时应进货多少个?解∶(1)商品的单价为50+x元,每个的利润是(50+x)-40元,销售量是500-10x个,则依题意得y=[(50+x)-40](500-10x),即y=-10x2+400x+5000.(2)依题意,得-10x2+400x+5000=8000.整理,得x2-40x+300=0.解得x1=10,x2=30.所以商品的单价应定为50+10=60(元)或50+30=80(元).当商品的单价为60元时,其进货量只能是500-10×10=400(个);当商品每个单价为80元时,其进货量只能是500-10×30=200(个) 抓利润关系,建立一元二次方程解决实际问题
三、运用新知,深化理解 设计意图
1. 水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为了保证每天至少售出260斤,张阿姨决定降价销售.(1)若将这种水果每斤的售价降低x元,则每天的销售量是 (100+200x) 斤(用含x的代数式表示);(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?、解:根据题意得:(4-2-x)(100+200x)=300,解得x=或x=1,当x=时,销售量是100+200×=200<260;当x=1时,销售量是100+200=300(斤),∵每天至少售出260斤,∴x=1.答:张阿姨需将每斤的售价降低1元. 要掌握关系式:利润=销售价-进价,从而得出:“卖出商品的利润=卖出一件商品的利润×卖出的件数”这个等量关系
四、师生互动、课堂小结 设计意图
利润计算模型:单件利润=卖价-进价总利润=单件利润X销售量列一元二次方程解应用题,审题是解决问题的基础,找等量关系列方程是关键,恰当灵活地设元直接影响着列方程与解法的难易,它可以为正确合理的答案提供有利的条件.方程的解必须进行实际题意的检验 先组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充.
五、学以致用
在某次聚会上,每两个人都握了一次手,所有人共握手10次.设有x个人参加这次聚会,则列方程为 =10 2.将进货价为40元的商品按50元售出时,每天能售出500个,经市场调查发现:该商品每涨价1元,其销售量减少10个.若一天能盈利8000元,则售价应定为(单位:元)( C )A.60 B.80C.60或80 D.703、某商店如果将进价为8元的商品按每件10元售出,每天可销售200件,已知这种商品每涨价0.5元,其销量减少10件.要使每天获得利润700元,若设售价为x元,则可列方程为( D )A.(10-8)(200-10x)=700 B.(10-8)(200+10x)=700C.(x-8)(200-20x)=700 D.(x-8)(400-20x)=7004、平方和等于110的三个连续正整数中,最大的一个是( C )A.5 B.6 C.7 D.85、一个两位数比它的个位上的数的平方小6,个位上的数与十位上的数的和是13.则这个两位数是58
教学反思
学习目标 知识与技能 使学生会用列一元二次方程的方法解应用题
过程与方法 让学生在经历运用一元二次方程解决一些代数问题的过程中体会一元二次方程的应用价值.
情感与态度 在应用一元二次方程的过程中,提高学生的分析问题、解决问题的能力
重点难点 重点:会熟练地列出一元二次方程解应用题。难点:将实际问抽象为一元二次方程的模型,利润计算问题
一、情景导入,初步认知 设计意图
1、一元二次方程模型与我们的生活密切相关,有广泛应用。2、利润计算问题:单件利润=卖价-进价 总利润=单件利润X销售量 由问题引入新课,提高学生学习兴趣
二、合作探究、获取新知 设计意图
动脑筋:将进货单价为40元的商品按50元售出时,能卖出500个,已知这种商品每个涨价1元,其销售量就减少10个,若这种商品涨价x元,则可赚得y元的利润.(1)写出x与y之间的关系式;(2)为了赚得8000元利润,售价应定为多少元,这时应进货多少个?解∶(1)商品的单价为50+x元,每个的利润是(50+x)-40元,销售量是500-10x个,则依题意得y=[(50+x)-40](500-10x),即y=-10x2+400x+5000.(2)依题意,得-10x2+400x+5000=8000.整理,得x2-40x+300=0.解得x1=10,x2=30.所以商品的单价应定为50+10=60(元)或50+30=80(元).当商品的单价为60元时,其进货量只能是500-10×10=400(个);当商品每个单价为80元时,其进货量只能是500-10×30=200(个) 抓利润关系,建立一元二次方程解决实际问题
三、运用新知,深化理解 设计意图
1. 水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为了保证每天至少售出260斤,张阿姨决定降价销售.(1)若将这种水果每斤的售价降低x元,则每天的销售量是 (100+200x) 斤(用含x的代数式表示);(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?、解:根据题意得:(4-2-x)(100+200x)=300,解得x=或x=1,当x=时,销售量是100+200×=200<260;当x=1时,销售量是100+200=300(斤),∵每天至少售出260斤,∴x=1.答:张阿姨需将每斤的售价降低1元. 要掌握关系式:利润=销售价-进价,从而得出:“卖出商品的利润=卖出一件商品的利润×卖出的件数”这个等量关系
四、师生互动、课堂小结 设计意图
利润计算模型:单件利润=卖价-进价总利润=单件利润X销售量列一元二次方程解应用题,审题是解决问题的基础,找等量关系列方程是关键,恰当灵活地设元直接影响着列方程与解法的难易,它可以为正确合理的答案提供有利的条件.方程的解必须进行实际题意的检验 先组内交流收获和感想,而后以小组为单位派代表进行总结.教师作以补充.
五、学以致用
在某次聚会上,每两个人都握了一次手,所有人共握手10次.设有x个人参加这次聚会,则列方程为 =10 2.将进货价为40元的商品按50元售出时,每天能售出500个,经市场调查发现:该商品每涨价1元,其销售量减少10个.若一天能盈利8000元,则售价应定为(单位:元)( C )A.60 B.80C.60或80 D.703、某商店如果将进价为8元的商品按每件10元售出,每天可销售200件,已知这种商品每涨价0.5元,其销量减少10件.要使每天获得利润700元,若设售价为x元,则可列方程为( D )A.(10-8)(200-10x)=700 B.(10-8)(200+10x)=700C.(x-8)(200-20x)=700 D.(x-8)(400-20x)=7004、平方和等于110的三个连续正整数中,最大的一个是( C )A.5 B.6 C.7 D.85、一个两位数比它的个位上的数的平方小6,个位上的数与十位上的数的和是13.则这个两位数是58
教学反思
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
