第三章 数据分析初步复习

课件31张PPT。第三章 数据分析初步复习 表示数据集中的统计量：平均数、中位数、众数；
表示数据离散的统计量：方差、标准差；平均数： （1）中位数与数据的排列位置有关，当
一组数据中的 个别数据相差较大时,
可用中位数来描述这组数据的集中趋势； 中位数：（2）计算方法：将一组数据按一定的顺序
排列起来，处于最中间位置的一个数
（或两个数的平均数）； 众数是对各数据出现频数的考察，
其大小只与数据中部分数据有关，它可
能是其中的一个数或多个数； 众 数：专题一 平均数、中位数、众数的计算例1、 求下面一组数据的平均数、中位数、众数
10 20 80 40 30 90 50 40 50 50 方法规律总结：根据数据的不同选择运用什么公式求平均数；
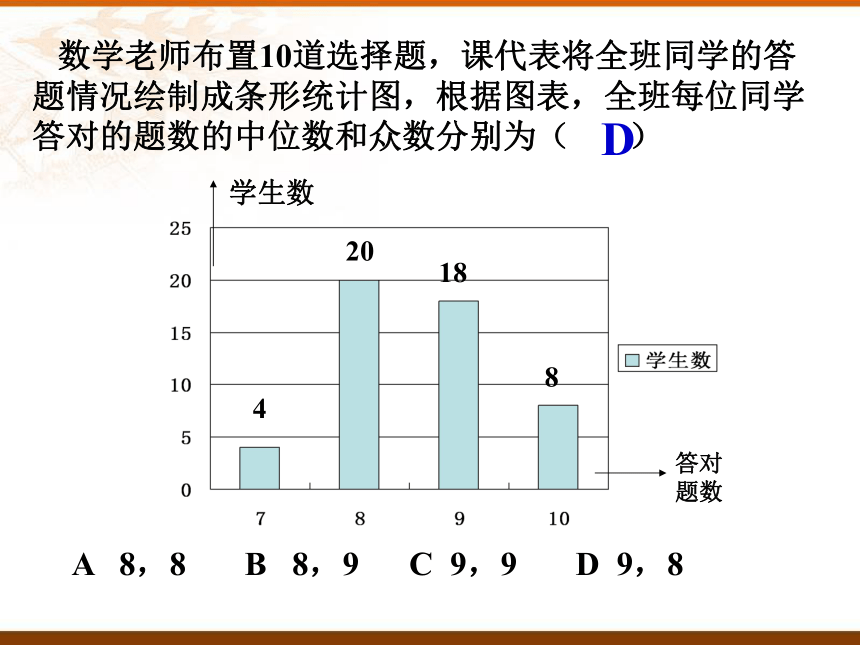
求中位数时，一定将数据按顺序进行摆列后再计算 10 20 30 40 40 50 50 50 80 90 中位数：取平均数，45 数学老师布置10道选择题，课代表将全班同学的答题情况绘制成条形统计图，根据图表，全班每位同学答对的题数的中位数和众数分别为（ ）学生数答对题数
DA 8，8 B 8，9 C 9，9 D 9，8420188做一做： 有人对展览馆七天中每天进馆参观的人数做了记录，情况如下：
180，176，176，173，176，181，182
求这组数据的中位数和众数。解：按从小到大的顺序排列为：
173，176，176，176，180，181，182，
则中位数为176，众数为176。中位数的优点计算简单，受极端值的影响较小，但不能充分利用所有数据的信息。众数是对各数据出现的频数的考察，其大小只与这组数据中的部分数据有关,但一组数据出现多个众数时,这时众数就没有多大的意义。 2. 在某城市,80%的家庭收入不少于2.5万元,下面一定不少于2.5万元的是( )A、年收入的平均数 B、年收入的众数
C、年收入的中位数 D、年收入的平均数和众数C３. 下列统计量不能反映一组数据集中程度的是
　　　　　　　　　　　　　　　( )A、平均数 B、众数
C、中位数 D、方差D 4. 某公司有1名经理和10名雇员，他们的月工资情况如下（单位：元）： 30000，2350，2350，2250，2250，2250，2250，2150，2050，1950，1850 上述数据的平均数是 元， 中位数是 元，众数是 元。通过上面得到的结果不难看出，用 （填“平均数”或“中位数、众数”）能更准确地反映该公司全体员工的月平均收入水平。47002250中位数或众数2250已知一组数据10，10，x，8(由大到小排列)的中位数与平均数相等，求x值及这组数据的中位数。 解：∵10，10，x,8的中位数与平均数相等
∴ (10+x)/2＝ (10+10+x+8)/4
∴x＝8
(10+x)/2＝9
∴这组数据中的中位数是9。挑战自我 反映一组数据的波动大小，计算公式： 方 差：标准差是方差的算术平方根，计算公式： 标准差：
例2、甲、乙两支礼仪队员的身高（单位：cm）如下：
甲队：178 177 179 179 178 178 177 178 177 179
乙队：178 177 179 178 178 180 180 178 176 176

哪支礼仪队更为整齐？你是怎样判断的？
专题二 方差、标准差的计算方法规律总结：方差越小、数据越稳定，波动也越小例3、选择恰当的统计量分析下面的问题:（1）某次数学考试,小明想知道自己的成绩是否处于中等水平。（3）数学老师对小明参加中考前的 5 次数学模拟考试成绩进行统计分析，判断小明的数学成绩是否稳定。（4）反映一组数据的平均水平。中位数众数方差或标准差平均数（2）为筹备班级联欢会，数学课代表对同学爱吃哪几种水果做民意测验，
假如你是班长，那么最终选什么水果，最值得观注的调查数据是什么校园生活我参与 比较甲、乙两名运动员一段时间内的测试成绩，下列情况中，说明甲的成绩较好的是（　　　　）B例5、
（1）一组数据5 7 7 x 中位数与平均数相等，则x的值为 。
（2）已知数据a、b、c 的平均数为8，那么数据a+1、b+2、c+3的平均数是 。
专题三 综合应用（3）已知某样本的方差是4，则这个样本的标准差 。5或9102（4）一组数据x1, x2,… xn, 的平均数是2，方差是3，
则一组新数据x1+8， x2+8，… xn+8的平均数是 ，方差是 .
另一组新数据3x1+8， 3x2+8，…3xn+8的平均数是 ，方差是 .1014273例6、某机械化养鸡场有一批同时开始饲养的良种鸡1000只，任取10只，称得质量情况如下：
求（1）这10只鸡的平均质量为多少？
（2）考虑到经济效益，该养鸡场规定质量在2.2千克以上（包括2.2千克）的鸡才可以出售，请估计这批鸡有多少只可以出售？专题四 综合应用 某公司招聘销售部经理，最后三名入选人员的成绩统计如下：80 90 100
98 96 80
80 90 1001.若按算术平均数排出名次，则谁将担任销售部经理？2.若按3:6:1求加权平均数，则谁将担任销售部经理？ 年收入 (万元)所占户数比 例7.某同学进行社会调查，随机抽查某地区20个家庭的收入情况，并绘制了统计图请根据统计图给出的信息回答：（1）填写下表 （2）数据中的中位数是————万元，众数是————万元。112345311.21.3这20个家庭的年平均收入为＿＿＿＿＿万元。1.6 5. 某公司招聘销售部经理，最后三名入选人员的成绩统计如下：80 90 100
98 96 80
80 90 1001.若按算术平均数排出名次，则谁将担任销售部经理？2.若按3:6:1求加权平均数，则谁将担任销售部经理？ 例4 某公司销售部有营销人员15人，销售部为了制订
某种商品的月销售定额，统计了这15人某月的销售量：（1）求这15位营销人员该月销售量的平均数、中位数
众数；
（2）假设销售部负责人把每位营销人员的销售量定为
320件，你认为是否合理？为什么？如果不合理，请你
制订一个较合理的销售定额，并说明理由。(1)平均数320件 ，中位数210件 ，众数210件（2）如果把每位营销人员的月销售量定为320件，
因为320件是一个平均销售量，其中有一个营销员
特别有能力，这个平均数受这个人的影响很大，而
中位数和众数都是210，因此，我们认为以210为规定
量比较科学。
练一练 某公司欲招业务经理一名，现对A，B，C
三名候选人进行三现测试，他们的各项测试成绩如下： （1）如果根据三项测试的平均成绩确定录用人选那么谁将
被录用？
（2）根据公司实际需要，公司将业务知识、创新实践和面试
三项得分按4：4：2的比例确定各人的测试成绩，此时谁将被
录用？解（1）A的平均成绩为（72+50+88）/3=70分
B的平均成绩为（85+74+45）/3=68分
C的平均成绩为（67+70+67）/3=68分
因此候选人A将被录用

（2）根据题意，3人的测试成绩如下：
A的测试成绩为66.4分
B的测试成绩为72.6分
C的测试成绩为68.2分
因此候选人B将被录用。
例5 一次科技知识竞赛，两组学生成绩如下：已经算得两个组的平均分都是80分，请根据你所学过的
统计知识，进一步判断这两个组这次竞赛中成绩谁优谁
次，并说明理由。分析：这是一题统计知识在实际生活中的应用，应从
几个统计量进行全方位的分析，如果单从方差等个别
特征值去分析会有失公正。解 (1).甲组成绩的众数是90分，乙组成绩的众数是70分
从众数看，甲组成绩好

(2).S2甲 =172,S2乙=256
因为 S2甲< S2乙 ,, 所以甲组成绩比乙组成绩稳定

(3) 甲乙两组成绩的中位数和平均数都是80分,其中甲
组成绩在80分以上(包括80分)的有33人,乙组成绩在80分以
上的有26人,从这一角度看甲组的总体成绩好

(4) 从成绩统计表看,甲组成绩高于90分的人数为20人,
乙组成绩高与90分的人为24人,所以乙组成绩高分多,同时
乙组满分的人数比甲组多6人,从这一角度看,乙组的成绩好方差与标准差：
反映一组数据的波动大小，标准差是方差的算术平方根，计算公式： 表示数据集中的统计量：平均数、中位数、众数；
表示数据离散的统计量：方差、标准差；ax1+b, ax2 +b, …,axn +b的平均数_______;方差为S=_______ax1, ax2, …, axn的平均数为_____; 方差为_____则x1+a, x2 +a, …,xn +a的平均数为____;方差为___.若x1, x2, …,xn的平均数为x，方差为s2，快速抢答s2a2 s2a2 s2则2x1-1, 2x2 -1, …,2xn -1的平均数为____;
方差为______；标准差为______.已知x1, x2, …,xn的平均数为8，方差为5，快速抢答1520谢谢合作再见