3.3立方根

课件13张PPT。立方根
2.当a≥0时，式 的意义各是什么? 答：1.如果一个数x的平方等于a, 即 那么x叫做a的平方根,表示为 .
正数有两个平方根,它们互为相反数,0的平方根是0,负数没有平方根. 2.当a≥0时, 表示a的算术平方根,
表示a的负的平方根, 表示a的平方根.
复习
1.平方根是如何定义的 ? 平方根有哪些性质?类比平方根的定义，你能否说出立方根的定义？新课
记作： .读作“三次根号a”，其中a是被开方数，3是根指数，且根指数3不能省略，否则与平方根混淆.
立方根的概念：
如果一个数的立方等于a，这个数就叫做a的立方根.（也叫做数a的三次方根）.
换句话说,如果 ,那么x叫做a的立方根或三次方根.
求一个数的立方根的运算叫做开立方.
2. 开立方例1 求下列各数的立方根：
(1)8； (2)－8；(3) 0.216； (4)－ ；(5) 0.
解: (1) ∵ ，
∴ 8的立方根是2，即 =2.
问：除2以外，还有什么数的立方等于8？ 就是说，正数8还有别的立方根吗？ 开立方与立方互为逆运算.
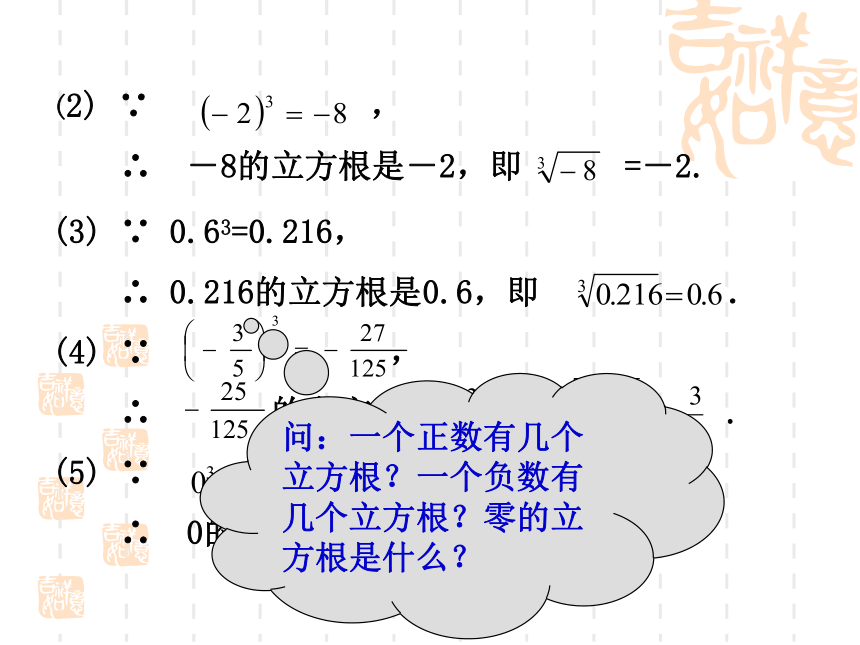
(3) ∵ 0.63=0.216，
∴ 0.216的立方根是0.6，即 ．
(4) ∵ ，
∴ 的立方根是 ，即 .
(5) ∵ ，
∴ 0的立方根是0，即 .
问：一个正数有几个立方根？一个负数有几个立方根？零的立方根是什么？
(2) ∵ ，
∴ －8的立方根是－2，即 =－2.

结论： 一个数的立方根是唯一的. 解： (1) ；(2) ； (3) ；

(4) ； (5) .
立方根的性质： 正数有一个正的立方根；负数有一个负的立方根；零的立方根仍旧是零.
例2 求下列各式的值：
(1) ；(2) ；(3) ；(4) ；(5) . 请同学们求出下列各式的值：
(1) ；(2) .解：思考：从上面的计算结果可以得到什么结论？ 答：一个负数的立方根等于它的绝对值的立方根的相反数.即：如果a>0，那么
由此得到：求一个负数的立方根的另一种方法，即可以先求出这个负数的绝对值的立方根，然后再取它的相反数.
例3 求下列各式的值(口答)
(1) ； (2) ；(3) .例4 求下列各式中的x:
(1) x3=0.125; (2) (10-x)3+54=0
解: (1)由x3=0.125，得 x= , ∴ x =0.5 .
(2)由 (10-x)3+54=0得, ，
∴
∴ ∴ x=16.
解 :(1) =-0.1 ;(2) = =10；
(3) = =-60.
测一测
练习1. 判断正误:
(1) 的立方根是 ；
(2)互为相反数的立方根互为相反数；
(3)任何数的立方根只有一个；
(4)如果一个数的平方根与其立方根相同，则 这个数是1；
(5)如果一个数的立方根是这个数的本身，那么这个数一定是零；
(6)一个数的立方根不是正数就是负数.(×)(×)(×)(×)(√)(√)4－7x≤0练习2. 填空:
(1) 64的平方根是________,
64的立方根是________.
(2) 的立方根是________.
(3) 是_______的立方根.
(4) 若 ,则 x=_______,
若 ,则 x=________.
(5) 若 , 则x的取值范围是__________,
若 有意义，则x的取值范围是_______________.
±3x取任意数 ±8 小 结：
1．知识点:
2．方法:（1）立方根的概念
(2）立方根的性质 (1)求一个数的立方根，通过立方运算来求.
(2) 遇到求负数的立方根问题，可转化为正数的立方根来解决，即通过 来实现.
(3)
3．注意问题 平方根与立方根的联系与区别联系:试一试
1.已知：x-2 的平方根是±2，2x+y+7 的
立方根是3，求 的平方根和立方根.
2.已知 ,
求 的值.
作业: P138 A组 2. 3.
思考：一个正方体的体积变为原来的n倍，它的棱长变为原来的多少倍？