2.2 一元二次方程的解法(1) 课件(共18张PPT)
文档属性
| 名称 | 2.2 一元二次方程的解法(1) 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 619.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-19 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
浙教版八下数学
2.2 一元二次方程的解法 (1)
---------------因式分解法
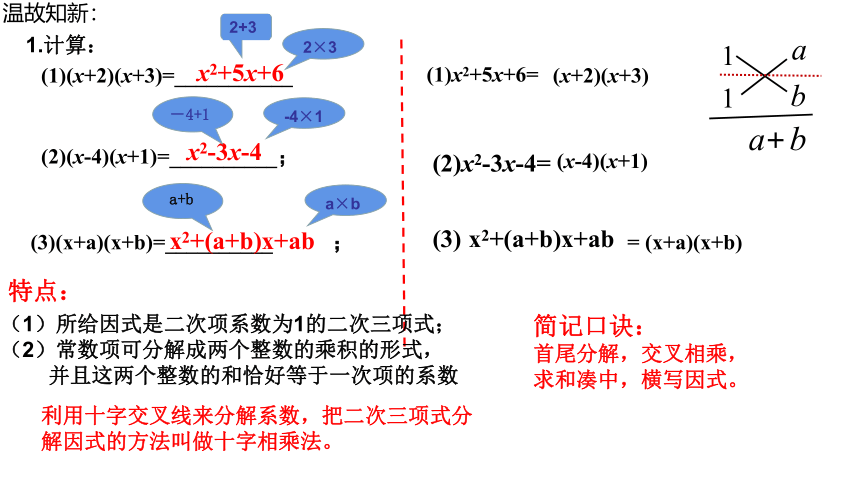
(1)(x+2)(x+3)=___________
x2+5x+6
(2)(x-4)(x+1)=__________;
(3)(x+a)(x+b)=__________ ;
x2-3x-4
x2+(a+b)x+ab
1.计算:
(1)x2+5x+6=
(x+2)(x+3)
(2)x2-3x-4=
(x-4)(x+1)
2+3
2×3
-4+1
-4×1
a+b
a×b
特点:
(1)所给因式是二次项系数为1的二次三项式;
(2)常数项可分解成两个整数的乘积的形式,
并且这两个整数的和恰好等于一次项的系数
简记口诀:
首尾分解,交叉相乘,
求和凑中,横写因式。
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法。
= (x+a)(x+b)
(3)
x2+(a+b)x+ab
温故知新:
2.把一个多项式变形成几个整式的乘积的形式,这种变形叫因式分解。
(1)提取公因式法:
am+bm+cm=m(a+b+c).
(2)公式法:
平方差公式:a2-b2=(a+b)(a-b),
完全平方公式:a2±2ab+b2=(a±b)2.
(3)十字相乘法:
x2+(a+b)x+ab=(x+a)(x+b).
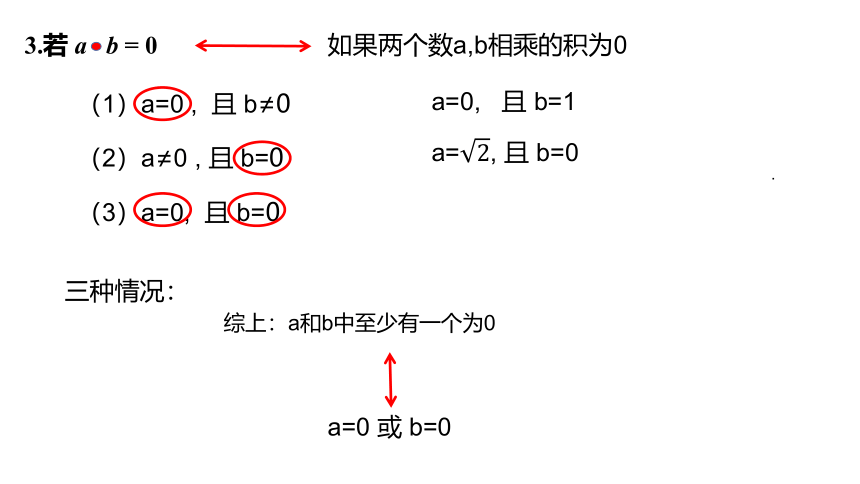
3.若 a b = 0
(1)a=0 , 且 b≠0
(2)a≠0 , 且 b=0
(3)a=0, 且 b=0
三种情况:
综上:a和b中至少有一个为0
a=0 或 b=0
如果两个数a,b相乘的积为0
a=0, 且 b=1
a=, 且 b=0
.
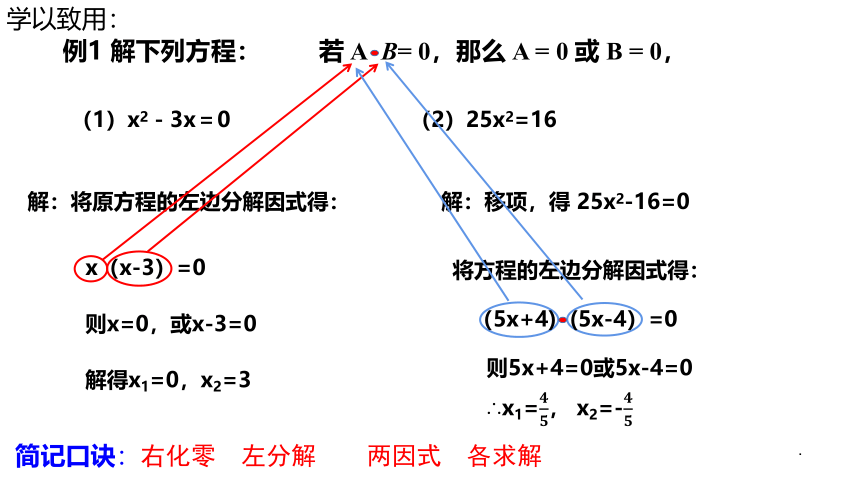
例1 解下列方程:
(1)x2-3x=0 (2)25x2=16
解:将原方程的左边分解因式得:
则x=0,或x-3=0
解得x1=0,x2=3
解:移项,得 25x2-16=0
将方程的左边分解因式得:
则5x+4=0或5x-4=0
若 A B= 0,那么 A = 0 或 B = 0,
∴x1=, x2=-
.
(5x+4) (5x-4)=0
x(x-3)=0
简记口诀:右化零 左分解 两因式 各求解
学以致用:
1.因式分解,使方程化为两个一次式的乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次.这种解一元二次方程的方法叫做因式分解法.
2.理论依据:“如果两个因式的积等于零,那么至少有一个因式等于零.”
3.“至少”有下列三层含义
① ② ③
.
归纳总结:
例2 解下列一元二次方程:
(1)(x-5) (3x-2)=10;
(2)(3x-4)2 = (4x-3)2.
移项、合并同类项得:3x2-17x=0.
将方程的左边分解因式,
得 x(3x-17)=0,
则x=0 ,或3x-17=0,
解:移项,得(3x-4)2-(4x-3)2=0.
将方程的左边分解因式,得
[(3x-4)+(4x-3)][(3x-4)-(4x-3)]=0,
即 (7x-7) (-x-1)=0.
则7x-7=0,或-x-1=0.
解得:x1=1, x2=-1.
解:去括号得:3x2-2x-15x+10=10
因式分解法口诀:右化零 左分解 两因式 各求解
解得:x1=0,x2=
.
例3 解方程:
表示一元二次方程有两个相等的实数根
则 (x-)2=0
.
归纳小结:
1.十字相乘法:
首尾分解,交叉相乘,
求和凑中,横写因式。
2.因式分解法:
右化零 左分解
两因式 各求解
3.“如果两个因式的积等于零,那么至少有一个因式等于零.”
1.用提取公因式法法解下列方程:
(1)提取公因式法:
am+bm+cm=m(a+b+c).
(1) 7x2=21x
(2) (x+2)2=2x+4
(3) 4(x-3)2-x(x-3)=0
(4) (x-2)2=2(x-2)
解:7x2-21x=0
7x(x-3)=0
7x=0 或x-3=0
x1=0,x2=3
解: (x+2)2-2(x+2)=0
(x+2)(x+2-2)=0
x+2=0 或x+2-2=0
x1=-2, x2=0
解:(x-3)[4(x-3)-x]=0
x-3=0 或3x-12=0
x1=3,x2=4
解:(x-2)2-2(x-2)=0
(x-2)(x-2-2)=0
x-2=0 或x-2-2=0
x1=2,x2=4
简记口诀:
右化零 左分解
两因式 各求解
夯实基础,稳扎稳打:
2.用平方差公式法解下列方程:
(3) (7x-1)2=4x2
(4) 9x2=(x-1)2
(1) x2 -25=0
(2) x2 -9=0
解:(x+5)(x-5)=0
x+5=0或x-5=0
x1=-5,x2=5
x1=-6,x2=6
解:(7x-1)2- 4x2=0
解: 9x2- (x-1)2=0
(7x-1+2x)(7x-1-2x)=0
(9x-1)(5x-1)=0
[3x+(x-1)][3x-(x-1)]=0
(4x-1)(2x+1)=0
9x-1=0或5x-1=0
4x-1=0或2x+1=0
平方差公式:a2-b2=(a+b)(a-b),
口诀:
右化零
左分解
两因式
各求解
解:(x+3)(x-3)=0
.
x+3=0x-3=0
.
x1=, x2=
.
x1=, x2= -
.
3.用完全平方公式法解下列方程:
(4) 27x2-18x= - 3
(1) x2+9= - 6x
(2) x(x - 4)= -4
(3) x2-2x= - 3
解:x2+6x+9=0
(x+3)2=0
x1=x2= -3
解:x2 - 4x+4=0
(x-2)2=0
x1=x2= 2
解:27x2-18x+3=0
9x2-6x+1=0
(3x-1)2=0
解:x2+2x+3=0
.
(x+)2=0
.
x1=x2= -
.
x1=x2=
.
完全平方公式:a2±2ab+b2=(a±b)2.
4.用十字相乘法解下列方程
1、x2-3x-10=0 2、(x+3)(x-1)=5
解:原方程可变形为
(x-5)(x+2)=0
x-5=0或x+2=0
∴ x1=5 ,x2=-2
解:原方程可变形为
x2+2x-8=0
(x-2)(x+4)=0
x-2=0或x+4=0
∴ x1=2 ,x2=-4
x
x
2
-5
x
x
4
-2
1.十字相乘法分解因式:
x2+(a+b)x+ab=
(x+a)(x+b).
x2+(a+b)x+ab=0
(x+a)(x+b)=0
2.十字相乘法解一元二次方程:
x+a=0
或x+b=0
竖分、
横写.
叉乘、
x
x
a
b
温馨提醒:
⑴2x2-5x-3=0; ⑵ 3x2+8x-3=0
x
3x
3
-1
x
2x
-3
1
竖分、叉乘、横写
拆两头,凑中间
连续递推,豁然开朗
5.用十字相乘法解下列方程
这样解是否正确呢?
不正确:方程的两边同时除以同一个不等于零的数,
所得的方程与原方程 同解。
解:方程的两边同时除以x,得 x=1
∴原方程的解为x=1
6: 解方程: x2=x
解:(1)当x=0时,左边=02=0,右边=0,
左边=右边,
∴x=0是原方程的解。
(2)当x≠0时,方程的两边同除以x,
得x=1
综上:原方程的解为:x1=1,x2=0.
7.一个数平方等于这个数本身,求这个数
(要求列出一元二次方程用因式分解法求解).
解:设这个数为x,根据题意,得
x2=x.
x2-x=0,
x(x-1) =0,
∴x=0, 或 x-1 =0
因式分解的方法,突出了转化的思想方法——“降次”,
鲜明地显示了“二次”转化为“一次”的过程.
8.用因式分解法解下列方程:
y1=0 ,
①y2=
.
(2) (3x+1)2-5=0
解:y(
.
y
.
.
y2
.
解: (3x+1)2-()2=0
.
(3x+1+)(3x+1-)=0
.
3x+1+3x+1-=0
.
x1=
.
x2=
.
浙教版八下数学
2.2 一元二次方程的解法 (1)
---------------因式分解法
(1)(x+2)(x+3)=___________
x2+5x+6
(2)(x-4)(x+1)=__________;
(3)(x+a)(x+b)=__________ ;
x2-3x-4
x2+(a+b)x+ab
1.计算:
(1)x2+5x+6=
(x+2)(x+3)
(2)x2-3x-4=
(x-4)(x+1)
2+3
2×3
-4+1
-4×1
a+b
a×b
特点:
(1)所给因式是二次项系数为1的二次三项式;
(2)常数项可分解成两个整数的乘积的形式,
并且这两个整数的和恰好等于一次项的系数
简记口诀:
首尾分解,交叉相乘,
求和凑中,横写因式。
利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法。
= (x+a)(x+b)
(3)
x2+(a+b)x+ab
温故知新:
2.把一个多项式变形成几个整式的乘积的形式,这种变形叫因式分解。
(1)提取公因式法:
am+bm+cm=m(a+b+c).
(2)公式法:
平方差公式:a2-b2=(a+b)(a-b),
完全平方公式:a2±2ab+b2=(a±b)2.
(3)十字相乘法:
x2+(a+b)x+ab=(x+a)(x+b).
3.若 a b = 0
(1)a=0 , 且 b≠0
(2)a≠0 , 且 b=0
(3)a=0, 且 b=0
三种情况:
综上:a和b中至少有一个为0
a=0 或 b=0
如果两个数a,b相乘的积为0
a=0, 且 b=1
a=, 且 b=0
.
例1 解下列方程:
(1)x2-3x=0 (2)25x2=16
解:将原方程的左边分解因式得:
则x=0,或x-3=0
解得x1=0,x2=3
解:移项,得 25x2-16=0
将方程的左边分解因式得:
则5x+4=0或5x-4=0
若 A B= 0,那么 A = 0 或 B = 0,
∴x1=, x2=-
.
(5x+4) (5x-4)=0
x(x-3)=0
简记口诀:右化零 左分解 两因式 各求解
学以致用:
1.因式分解,使方程化为两个一次式的乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次.这种解一元二次方程的方法叫做因式分解法.
2.理论依据:“如果两个因式的积等于零,那么至少有一个因式等于零.”
3.“至少”有下列三层含义
① ② ③
.
归纳总结:
例2 解下列一元二次方程:
(1)(x-5) (3x-2)=10;
(2)(3x-4)2 = (4x-3)2.
移项、合并同类项得:3x2-17x=0.
将方程的左边分解因式,
得 x(3x-17)=0,
则x=0 ,或3x-17=0,
解:移项,得(3x-4)2-(4x-3)2=0.
将方程的左边分解因式,得
[(3x-4)+(4x-3)][(3x-4)-(4x-3)]=0,
即 (7x-7) (-x-1)=0.
则7x-7=0,或-x-1=0.
解得:x1=1, x2=-1.
解:去括号得:3x2-2x-15x+10=10
因式分解法口诀:右化零 左分解 两因式 各求解
解得:x1=0,x2=
.
例3 解方程:
表示一元二次方程有两个相等的实数根
则 (x-)2=0
.
归纳小结:
1.十字相乘法:
首尾分解,交叉相乘,
求和凑中,横写因式。
2.因式分解法:
右化零 左分解
两因式 各求解
3.“如果两个因式的积等于零,那么至少有一个因式等于零.”
1.用提取公因式法法解下列方程:
(1)提取公因式法:
am+bm+cm=m(a+b+c).
(1) 7x2=21x
(2) (x+2)2=2x+4
(3) 4(x-3)2-x(x-3)=0
(4) (x-2)2=2(x-2)
解:7x2-21x=0
7x(x-3)=0
7x=0 或x-3=0
x1=0,x2=3
解: (x+2)2-2(x+2)=0
(x+2)(x+2-2)=0
x+2=0 或x+2-2=0
x1=-2, x2=0
解:(x-3)[4(x-3)-x]=0
x-3=0 或3x-12=0
x1=3,x2=4
解:(x-2)2-2(x-2)=0
(x-2)(x-2-2)=0
x-2=0 或x-2-2=0
x1=2,x2=4
简记口诀:
右化零 左分解
两因式 各求解
夯实基础,稳扎稳打:
2.用平方差公式法解下列方程:
(3) (7x-1)2=4x2
(4) 9x2=(x-1)2
(1) x2 -25=0
(2) x2 -9=0
解:(x+5)(x-5)=0
x+5=0或x-5=0
x1=-5,x2=5
x1=-6,x2=6
解:(7x-1)2- 4x2=0
解: 9x2- (x-1)2=0
(7x-1+2x)(7x-1-2x)=0
(9x-1)(5x-1)=0
[3x+(x-1)][3x-(x-1)]=0
(4x-1)(2x+1)=0
9x-1=0或5x-1=0
4x-1=0或2x+1=0
平方差公式:a2-b2=(a+b)(a-b),
口诀:
右化零
左分解
两因式
各求解
解:(x+3)(x-3)=0
.
x+3=0x-3=0
.
x1=, x2=
.
x1=, x2= -
.
3.用完全平方公式法解下列方程:
(4) 27x2-18x= - 3
(1) x2+9= - 6x
(2) x(x - 4)= -4
(3) x2-2x= - 3
解:x2+6x+9=0
(x+3)2=0
x1=x2= -3
解:x2 - 4x+4=0
(x-2)2=0
x1=x2= 2
解:27x2-18x+3=0
9x2-6x+1=0
(3x-1)2=0
解:x2+2x+3=0
.
(x+)2=0
.
x1=x2= -
.
x1=x2=
.
完全平方公式:a2±2ab+b2=(a±b)2.
4.用十字相乘法解下列方程
1、x2-3x-10=0 2、(x+3)(x-1)=5
解:原方程可变形为
(x-5)(x+2)=0
x-5=0或x+2=0
∴ x1=5 ,x2=-2
解:原方程可变形为
x2+2x-8=0
(x-2)(x+4)=0
x-2=0或x+4=0
∴ x1=2 ,x2=-4
x
x
2
-5
x
x
4
-2
1.十字相乘法分解因式:
x2+(a+b)x+ab=
(x+a)(x+b).
x2+(a+b)x+ab=0
(x+a)(x+b)=0
2.十字相乘法解一元二次方程:
x+a=0
或x+b=0
竖分、
横写.
叉乘、
x
x
a
b
温馨提醒:
⑴2x2-5x-3=0; ⑵ 3x2+8x-3=0
x
3x
3
-1
x
2x
-3
1
竖分、叉乘、横写
拆两头,凑中间
连续递推,豁然开朗
5.用十字相乘法解下列方程
这样解是否正确呢?
不正确:方程的两边同时除以同一个不等于零的数,
所得的方程与原方程 同解。
解:方程的两边同时除以x,得 x=1
∴原方程的解为x=1
6: 解方程: x2=x
解:(1)当x=0时,左边=02=0,右边=0,
左边=右边,
∴x=0是原方程的解。
(2)当x≠0时,方程的两边同除以x,
得x=1
综上:原方程的解为:x1=1,x2=0.
7.一个数平方等于这个数本身,求这个数
(要求列出一元二次方程用因式分解法求解).
解:设这个数为x,根据题意,得
x2=x.
x2-x=0,
x(x-1) =0,
∴x=0, 或 x-1 =0
因式分解的方法,突出了转化的思想方法——“降次”,
鲜明地显示了“二次”转化为“一次”的过程.
8.用因式分解法解下列方程:
y1=0 ,
①y2=
.
(2) (3x+1)2-5=0
解:y(
.
y
.
.
y2
.
解: (3x+1)2-()2=0
.
(3x+1+)(3x+1-)=0
.
3x+1+3x+1-=0
.
x1=
.
x2=
.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
