27.2.1 二次函数y=ax2的图象和性质课件
文档属性
| 名称 | 27.2.1 二次函数y=ax2的图象和性质课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-27 00:00:00 | ||
图片预览




文档简介
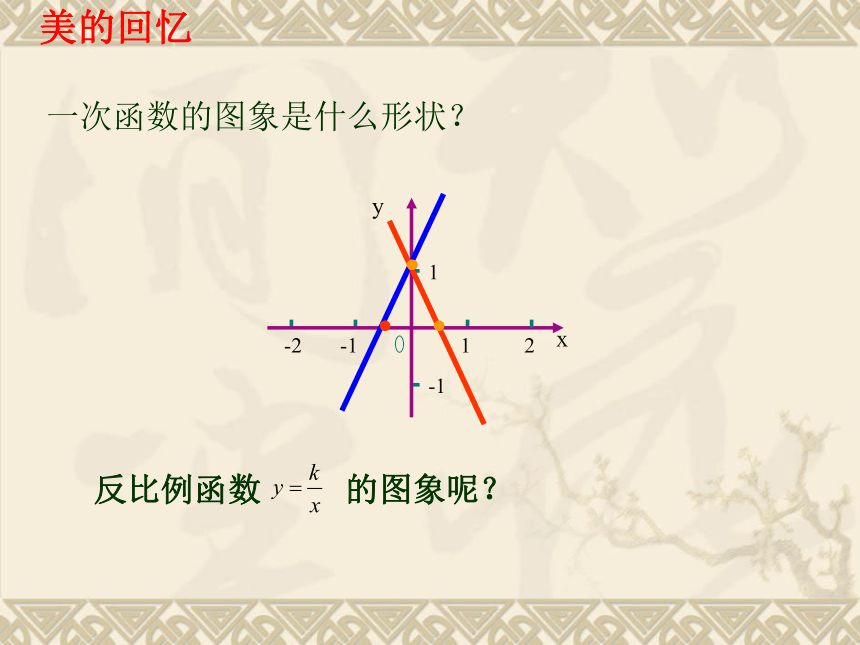
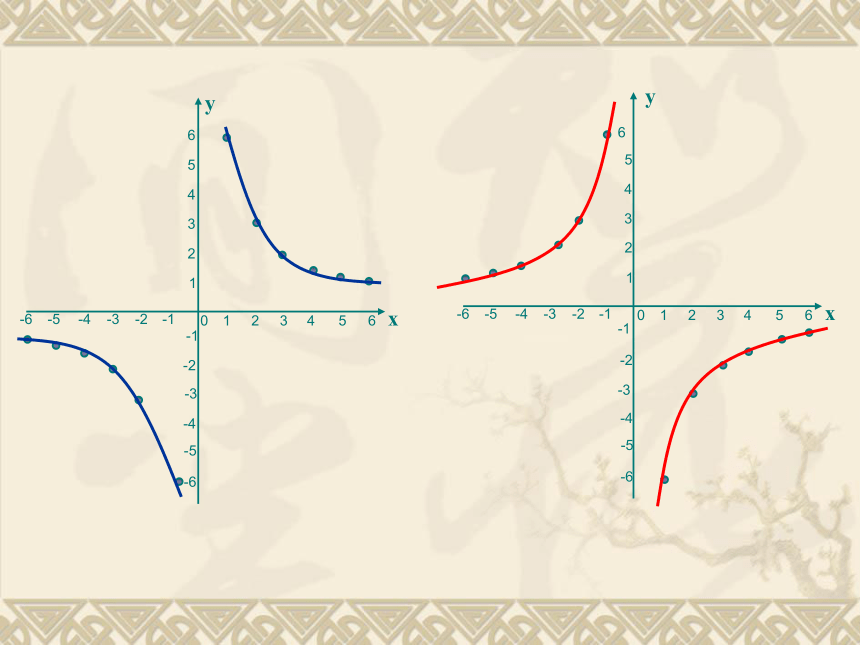
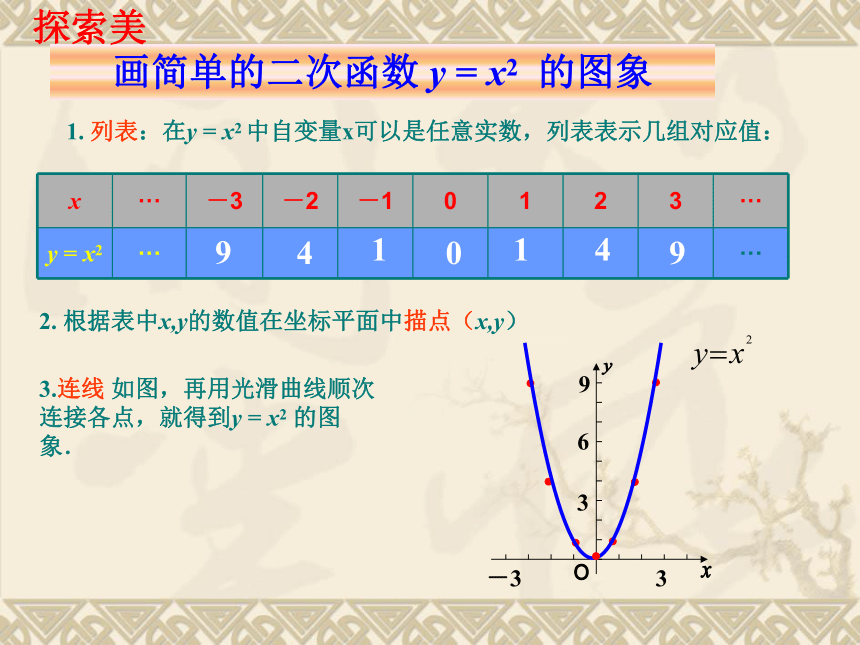
课件20张PPT。 二次函数y=ax2的图象和性质????反比例函数 的图象呢?美的回忆一次函数的图象是什么形状?123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy1. 列表:在y = x2 中自变量x可以是任意实数,列表表示几组对应值:2. 根据表中x,y的数值在坐标平面中描点(x,y)画简单的二次函数 y = x2 的图象01491493.连线 如图,再用光滑曲线顺次连接各点,就得到y = x2 的图象.探索美 二次函数 y = x2的图象是一条曲线,它的形状类似于投球时球在空中所经过的路线,只是这条曲线开口向上,这条曲线叫做抛物线 y = x2 , 看出:y轴是抛物线y = x 2 的对称轴,抛物线y = x 2 与它的对称轴的交点(0,0)叫做抛物线y = x2 的顶点,它是抛物线y = x 2 的最低点. 在同一直角坐标系中,画出函数 的图象.分别填表,画出它们的图象,如图4.5820.5084.520.5相同点
开口:向上,
顶 点:原点(0,0)——最低点
对称轴: y 轴
增减性(1)y 轴左侧,抛物线从左至右下降。(x<0时y随x增大而减小);(2)y 轴右侧,抛物线从左至右上升(x>0时y随x增大而增大)
不同点:a 值越大,抛物线的开口越小.-4.5-8-2-0.50-8-4.5-2-0.5自己动手画出函数 y= - x2, 的图象。y= - x2请找出相同点与不同点:例题与练习应用美1、根据已画好的函数图象填空:
(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,在 侧, y随着x的增大而增大;在 侧,y随着x的增大而减小,当x= 时,函数y的值最小,最小值是 ,抛物线y=2x2在x轴的 方(除顶点外)。2、不画图象,说出抛物线y=-4x2与y= x2的开口方向、对称轴、顶点、增减性。(0,0)y轴y轴右y轴左00上比较函数 的图象,函数 的图象。你发现 与 有什么关系?
y=x2y=2x2y=-x2y=-2x2请同学们把所学的二次函数图象的知识归纳小结。yyyyxxa<0xxa>0y轴右侧x>0y轴左侧x<0图象开口方向对称轴顶点y=ax2增大(0,0)
最低点(0,0)
最高点y轴y轴向上向下增大减小增大增大增大减小增大|a|越大,抛物线的开口越小;最
值最小值
0最大值
0动手做一做:抛物线 如何变换得到抛物线 。
第七页“练习”第1,4题。
作业布置创造美xy再
见
开口:向上,
顶 点:原点(0,0)——最低点
对称轴: y 轴
增减性(1)y 轴左侧,抛物线从左至右下降。(x<0时y随x增大而减小);(2)y 轴右侧,抛物线从左至右上升(x>0时y随x增大而增大)
不同点:a 值越大,抛物线的开口越小.-4.5-8-2-0.50-8-4.5-2-0.5自己动手画出函数 y= - x2, 的图象。y= - x2请找出相同点与不同点:例题与练习应用美1、根据已画好的函数图象填空:
(1)抛物线y=2x2的顶点坐标是 ,对称轴是 ,在 侧, y随着x的增大而增大;在 侧,y随着x的增大而减小,当x= 时,函数y的值最小,最小值是 ,抛物线y=2x2在x轴的 方(除顶点外)。2、不画图象,说出抛物线y=-4x2与y= x2的开口方向、对称轴、顶点、增减性。(0,0)y轴y轴右y轴左00上比较函数 的图象,函数 的图象。你发现 与 有什么关系?
y=x2y=2x2y=-x2y=-2x2请同学们把所学的二次函数图象的知识归纳小结。yyyyxxa<0xxa>0y轴右侧x>0y轴左侧x<0图象开口方向对称轴顶点y=ax2增大(0,0)
最低点(0,0)
最高点y轴y轴向上向下增大减小增大增大增大减小增大|a|越大,抛物线的开口越小;最
值最小值
0最大值
0动手做一做:抛物线 如何变换得到抛物线 。
第七页“练习”第1,4题。
作业布置创造美xy再
见
