2.3.2一元二次方程的应用 同步练习(含解析)
文档属性
| 名称 | 2.3.2一元二次方程的应用 同步练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-20 10:09:55 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版(2012)八年级数学下册 同步练习
2.3.1一元二次方程的应用
一、选择题
1.如图,要把长为5m,宽为3m的矩形花坛四周扩展相同的宽度x m,得到面积为的新矩形花坛,则根据题意可列方程为 ( )
A. B.
C. D.
2.如图,某小区居民休闲娱乐中心是一块长方形(长30米,宽20米)场地,被3条宽度相等的绿化带分为总面积为480平方米的活动场所(羽毛球,乒乓球)如果设绿化带的宽度为米,由题意可列方程为
A. B. C. D.
3.如图,在中,,,.动点,分别从点,同时开始移动,点的速度为秒,点的速度为秒,点移动到点后停止,点也随之停止运动.下列时间瞬间中,能使面积为的是 ( )
A.2秒钟 B.3秒钟 C.4秒钟 D.5秒钟
4.如图所示,A,B,C,D为矩形的四个顶点,AB=16cm,AD=8cm,动点P,Q分别从点A,C同时出发,点P以3cm/s的速度向B移动,一直到达B为止;点Q以2cm/s的速度向D移动.当P,Q两点从出发开始几秒时,点P和点Q的距离是10cm.(若一点到达终点,另一点也随之停止运动) ( )
A.2s或s B.1s或s C.s D.2s或s
5.第二十二届世界杯足球赛将于2022年11月20日在卡塔尔举办开幕赛,为了迎接世界杯的到来,某市举行了足球邀请赛,规定参赛的每两个队之间比赛一场,共安排了60场比赛.设比赛组织者邀请了x个队参赛,则下列方程正确的是 ( )
A. B. C. D.
二、填空题
6.如图,是由三个边长分别为6,9,x的正方形所组成的图形,若直线将它分成面积相等的两部分,则x的值是___________.
7.如图,将一块正方形空地划出部分区域进行绿化,原正方形空地一边减少了,另一边减少了,剩余一块面积为的矩形空地,则原正方形空地的边长是________.
8.如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动,设运动的时间为t秒,有一点到终点运动即停止,当t=___时,S△DPQ=28cm2.
9.如图,点在线段上,在线段上,且,,,若则的长为______.
10.如图.有一块长20cm,宽10cm的长方形铁皮,若在铁皮的四个角上各截去一个相同的小正方形,然后把凸出部分折起来,做成一个底面积为的无盖的长方体盒子,则这个盒子的高为____________cm.
三、解答题
11.如图,某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为),另外三面用栅栏围成,已知栅栏总长度为,设矩形垂直于墙的一边,即的长为.若矩形养殖场的面积为,求此时的的值.
12.如图,在一块长12m,宽8m的矩形空地上,修建同样宽的两条道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,且栽种花草的面积为60m2,求道路的宽是多少米?
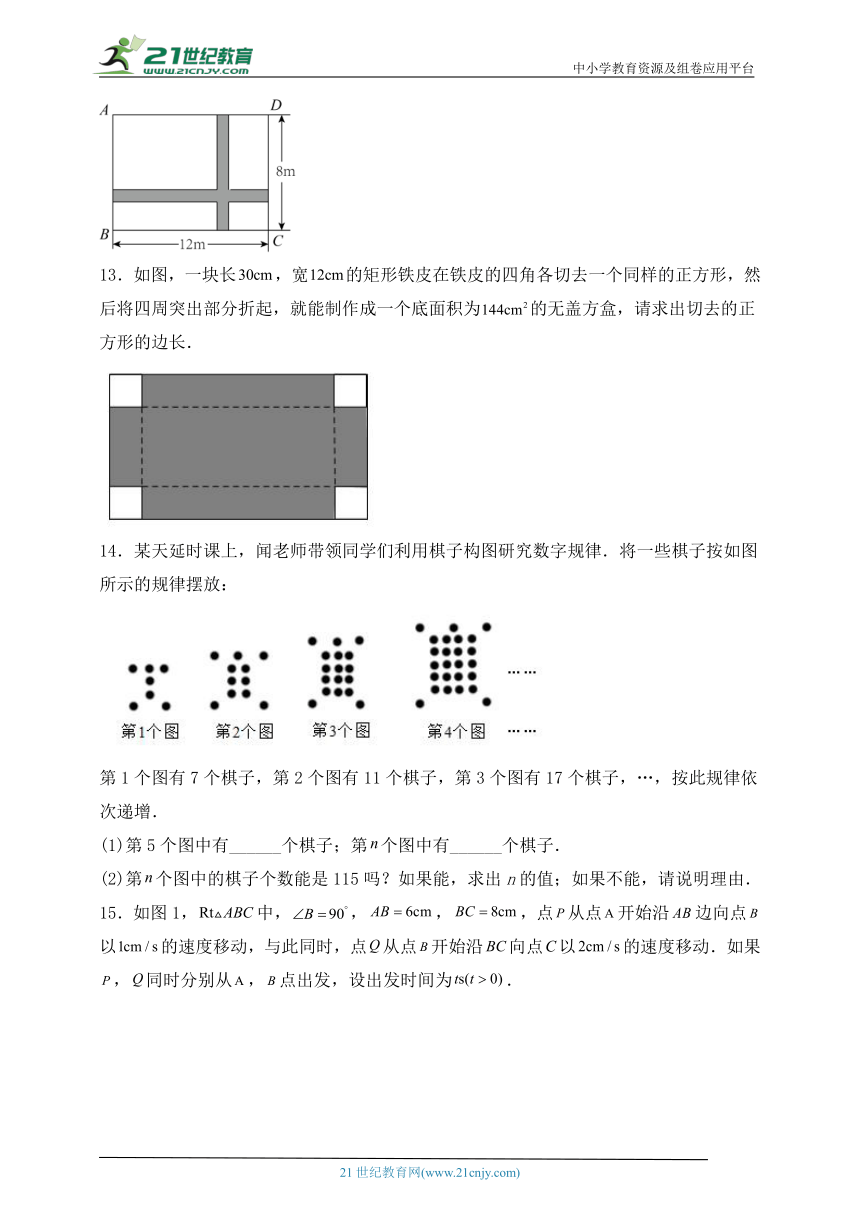
13.如图,一块长,宽的矩形铁皮在铁皮的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作成一个底面积为的无盖方盒,请求出切去的正方形的边长.
14.某天延时课上,闻老师带领同学们利用棋子构图研究数字规律.将一些棋子按如图所示的规律摆放:
第1个图有7个棋子,第2个图有11个棋子,第3个图有17个棋子,…,按此规律依次递增.
(1)第5个图中有______个棋子;第个图中有______个棋子.
(2)第个图中的棋子个数能是115吗?如果能,求出n的值;如果不能,请说明理由.
15.如图1,中,,,,点从点开始沿边向点以的速度移动,与此同时,点从点开始沿向点以的速度移动.如果,同时分别从,点出发,设出发时间为.
(1)当为何值时,的面积是?
(2)当为何值时,点和点间的距离是?
(3)如图2,若点,点同时从点出发,点沿折线移动,点沿折线移动,其余条件均不变,求当,在点相遇时,点与点的距离.
参考答案:
1.D
【分析】拓展后的长为:m,宽为m,根据矩形面积公式列方程即可.
【解析】解:依题意,拓展后的长为:m,宽为m,
则有,
故选:D.
【点睛】本题考查了一元二次方程的应用;解题的关键是会求拓展后的长和宽.
2.B
【分析】分别表示绿化带的长和宽分别为m和m,根据长方形面积公式列出方程;
【解析】解:根据题意得,绿化带的长和宽就分别为m和m,
所以方程为,
,
故选:B.
【点睛】本题考查一元二次方程的实际应用,解题关键表示出绿化带的长和宽.
3.B
【分析】设出动点,运动秒,能使的面积为,用分别表示出和的长,利用三角形的面积计算公式即可解答.
【解析】解:设动点,运动秒后,能使的面积为,
则为,为,由三角形的面积计算公式列方程得,
,
解得,(当时,,不合题意,舍去).
动点,运动3秒时,能使的面积为.
故选:B.
【点睛】此题考查一元二次方程的应用,图形中的动点问题,根据题意,列出方程是关键.
4.D
【分析】设当P、Q两点从出发开始到x秒时,点P和点Q的距离是10cm,此时AP=3xcm,DQ=(16-2x)cm,利用勾股定理即可得出关于x的一元二次方程,解之即可得出结论.
【解析】解:设当P、Q两点从出发开始到xs时,点P和点Q的距离是10cm,此时AP=3xcm,DQ=(16-2x)cm,
根据题意得:(16-2x-3x)2+82=102,
解得:x1=2,x2=,
答:当P、Q两点从出发开始到2s或s时,点P和点Q的距离是10cm.
故选:D.
【点睛】本题考查了一元二次方程的应用以及勾股定理,利用勾股定理找出关于x的一元二次方程是解题的关键.
5.D
【分析】根据题意参赛的每两个队之间比赛一场,每个球队需要比赛场,x个队参赛需要参赛,但是两个球队不重复比赛,所以乘以,即可解得.
【解析】根据题意得:
,
故选:D.
【点睛】此题考查了一元二次方程解应用题,解题的关键是根据题意找出等量关系式.
6.3或6
【分析】延长交于点C,延长交于点D,可得四边形是矩形,依据与面积相等,线段将三个正方形分成面积相等的两部分,即可得到四边形与四边形的面积相等,进而得到x的值.
【解析】解:如图所示,延长交于点C,延长交于点D,则四边形是矩形,
∴与面积相等,
又∵线段将三个正方形分成面积相等的两部分,
∴四边形与四边形的面积相等,
∴,
解得或6,
故答案为:3或6.
【点睛】此题考查一元二次方程的实际应用,矩形的性质,正方形的性质,题中的辅助线的引入是难点.
7.10
【分析】本题可设原正方形的边长为,则剩余的空地长为,宽为.根据长方形的面积公式方程可列出,进而可求出原正方形的边长.
【解析】解:设原正方形的边长为,依题意得:
,
解得:,(不合题意,舍去),
故原正方形的边长.
故答案是:10.
【点睛】本题考查一元二次方程的应用.正确记忆长方形的面积公式,求得剩余的空地的长和宽是解决本题的关键.
8.2或4
【分析】由题意可知当运动时间为t秒时,则AP=t cm,BP=(6-t)cm,BQ=2t cm,CQ=(12-2t)cm,根据S△DPQ=28cm2,即可得出关于t的一元二次方程,解之即可得出答案.
【解析】解:当运动时间为t秒时,则AP=t cm,BP=(6-t)cm,BQ=2t cm,CQ=(12-2t)cm,
依题意得:12×6-×12t-×6(12-2t)-×2t (6-t)=28,
整理得:t2-6t+8=0,
解得:t1=2,t2=4.
故答案为:2或4.
【点睛】本题考查一元二次方程的几何应用与矩形的性质,找准等量关系,正确列出一元二次方程是解题的关键.
9.
【分析】根据,有,再根据,可得,即,解方程即可求解,问题随之得解.
【解析】∵,
∴,
∵,
∴,即,
解得:(负值舍去),
∵,
∴,
故答案为:.
【点睛】本题主要考查了一元二次方程的应用,根据题意得到关于的一元二次方程是解答本题的关键.
10.2
【分析】设这个盒子的高为x cm,则做成的无盖长方体的底面长为(20 2x)cm,宽为(10 2x)cm,根据无盖长方体盒子的底面积为,即可得出关于x的一元二次方程,解之即可得出x的值,再结合盒子的高为正值,即可解答.
【解析】解:设这个盒子的高为x cm,则做成的无盖长方体的底面长为cm,宽为cm,
依题意得:,
整理得:,
解得:,.
又∵,
∴,
∴,
故答案为:2.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
11.的值为
【分析】根据各边之间的关系,可得出的长为,根据矩形养殖场的面积为,可得出关于的一元二次方程,解之取其符合题意的值,即可得出结论.
【解析】解:∵栅栏总长度为,的长为,
∴的长为.
根据题意得:,整理得:,
解得:,,
当时,,不符合题意,舍去;
当时,,符合题意.
∴此时的值为.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
12.2m.
【分析】把所修的两条道路分别平移到矩形的最上边和最左边,则剩下的部分是一个长方形,根据长方形的面积公式列方程即可.
【解析】解:设道路的宽应为x米,剩余部分拼成一个长方形,长和宽分别为(12﹣x)米、(8﹣x)米,
由题意得,(12﹣x)(8﹣x)=60.
解得x=2或x=18(舍去).
答:道路的宽应设计为2m.
【点睛】此题主要考查了一元二次方程的应用,把中间修建的两条道路分别平移到矩形地面的最上边和最左边是做本题的关键.
13.
【分析】设切去的正方形的边长为,根据制作成一个底面积为的无盖方盒列出等量关系式即可解得.
【解析】解:设切去的正方形的边长为,
,(舍去)
答:去的正方形的边长为.
【点睛】此题考查了一元二次的方程的实际应用,解题的关键是根据题意列出等量关系式.
14.(1);
(2)能,第10个图中的棋子个数为115.
【分析】(1)先观察得出图形变化中的规律,再利用规律求解即可;
(2)令建立方程求解,检验n的值是否符合题意,即可求解.
【解析】(1)第1个图:,
第2个图:,
第3个图:,
…
第5个图:,
由图中规律可知,第个图:,
故答案为:;.
(2)令,
解得(舍去),,
∴能,第10个图中的棋子个数为115.
【点睛】本题考查了图形规律题,涉及到了一元二次方程的应用,解题关键是发现图中的变化规律,并能用数式进行表示.
15.(1)2s或4s;(2);(3)
【分析】(1)根据题意表示出BP,BQ,然后利用列出方程,解方程即可;
(2)根据勾股定理列出一个关于t的一元二次方程,解方程即可得出答案;
(3)首先根据勾股定理求出AC的长,作于点E,连接DB,则DE可求,进而利用勾股定理求出AE的长度,则可得出DE的长度,最后再利用勾股定理即可求解.
【解析】(1)根据题意有,
,
,
,
解得或,
∴当t为2s或4s时,的面积是;
(2)∵,
,
即,
解得或(舍去),
∴当时,点和点间的距离是;
(3)∵,
.
根据题意得,
解得,
∴.
作于点E,连接DB,
则 ,
,
,
.
【点睛】本题主要考查三角形中的动点问题,掌握勾股定理,一元二次方程的解法是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版(2012)八年级数学下册 同步练习
2.3.1一元二次方程的应用
一、选择题
1.如图,要把长为5m,宽为3m的矩形花坛四周扩展相同的宽度x m,得到面积为的新矩形花坛,则根据题意可列方程为 ( )
A. B.
C. D.
2.如图,某小区居民休闲娱乐中心是一块长方形(长30米,宽20米)场地,被3条宽度相等的绿化带分为总面积为480平方米的活动场所(羽毛球,乒乓球)如果设绿化带的宽度为米,由题意可列方程为
A. B. C. D.
3.如图,在中,,,.动点,分别从点,同时开始移动,点的速度为秒,点的速度为秒,点移动到点后停止,点也随之停止运动.下列时间瞬间中,能使面积为的是 ( )
A.2秒钟 B.3秒钟 C.4秒钟 D.5秒钟
4.如图所示,A,B,C,D为矩形的四个顶点,AB=16cm,AD=8cm,动点P,Q分别从点A,C同时出发,点P以3cm/s的速度向B移动,一直到达B为止;点Q以2cm/s的速度向D移动.当P,Q两点从出发开始几秒时,点P和点Q的距离是10cm.(若一点到达终点,另一点也随之停止运动) ( )
A.2s或s B.1s或s C.s D.2s或s
5.第二十二届世界杯足球赛将于2022年11月20日在卡塔尔举办开幕赛,为了迎接世界杯的到来,某市举行了足球邀请赛,规定参赛的每两个队之间比赛一场,共安排了60场比赛.设比赛组织者邀请了x个队参赛,则下列方程正确的是 ( )
A. B. C. D.
二、填空题
6.如图,是由三个边长分别为6,9,x的正方形所组成的图形,若直线将它分成面积相等的两部分,则x的值是___________.
7.如图,将一块正方形空地划出部分区域进行绿化,原正方形空地一边减少了,另一边减少了,剩余一块面积为的矩形空地,则原正方形空地的边长是________.
8.如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动,设运动的时间为t秒,有一点到终点运动即停止,当t=___时,S△DPQ=28cm2.
9.如图,点在线段上,在线段上,且,,,若则的长为______.
10.如图.有一块长20cm,宽10cm的长方形铁皮,若在铁皮的四个角上各截去一个相同的小正方形,然后把凸出部分折起来,做成一个底面积为的无盖的长方体盒子,则这个盒子的高为____________cm.
三、解答题
11.如图,某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为),另外三面用栅栏围成,已知栅栏总长度为,设矩形垂直于墙的一边,即的长为.若矩形养殖场的面积为,求此时的的值.
12.如图,在一块长12m,宽8m的矩形空地上,修建同样宽的两条道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,且栽种花草的面积为60m2,求道路的宽是多少米?
13.如图,一块长,宽的矩形铁皮在铁皮的四角各切去一个同样的正方形,然后将四周突出部分折起,就能制作成一个底面积为的无盖方盒,请求出切去的正方形的边长.
14.某天延时课上,闻老师带领同学们利用棋子构图研究数字规律.将一些棋子按如图所示的规律摆放:
第1个图有7个棋子,第2个图有11个棋子,第3个图有17个棋子,…,按此规律依次递增.
(1)第5个图中有______个棋子;第个图中有______个棋子.
(2)第个图中的棋子个数能是115吗?如果能,求出n的值;如果不能,请说明理由.
15.如图1,中,,,,点从点开始沿边向点以的速度移动,与此同时,点从点开始沿向点以的速度移动.如果,同时分别从,点出发,设出发时间为.
(1)当为何值时,的面积是?
(2)当为何值时,点和点间的距离是?
(3)如图2,若点,点同时从点出发,点沿折线移动,点沿折线移动,其余条件均不变,求当,在点相遇时,点与点的距离.
参考答案:
1.D
【分析】拓展后的长为:m,宽为m,根据矩形面积公式列方程即可.
【解析】解:依题意,拓展后的长为:m,宽为m,
则有,
故选:D.
【点睛】本题考查了一元二次方程的应用;解题的关键是会求拓展后的长和宽.
2.B
【分析】分别表示绿化带的长和宽分别为m和m,根据长方形面积公式列出方程;
【解析】解:根据题意得,绿化带的长和宽就分别为m和m,
所以方程为,
,
故选:B.
【点睛】本题考查一元二次方程的实际应用,解题关键表示出绿化带的长和宽.
3.B
【分析】设出动点,运动秒,能使的面积为,用分别表示出和的长,利用三角形的面积计算公式即可解答.
【解析】解:设动点,运动秒后,能使的面积为,
则为,为,由三角形的面积计算公式列方程得,
,
解得,(当时,,不合题意,舍去).
动点,运动3秒时,能使的面积为.
故选:B.
【点睛】此题考查一元二次方程的应用,图形中的动点问题,根据题意,列出方程是关键.
4.D
【分析】设当P、Q两点从出发开始到x秒时,点P和点Q的距离是10cm,此时AP=3xcm,DQ=(16-2x)cm,利用勾股定理即可得出关于x的一元二次方程,解之即可得出结论.
【解析】解:设当P、Q两点从出发开始到xs时,点P和点Q的距离是10cm,此时AP=3xcm,DQ=(16-2x)cm,
根据题意得:(16-2x-3x)2+82=102,
解得:x1=2,x2=,
答:当P、Q两点从出发开始到2s或s时,点P和点Q的距离是10cm.
故选:D.
【点睛】本题考查了一元二次方程的应用以及勾股定理,利用勾股定理找出关于x的一元二次方程是解题的关键.
5.D
【分析】根据题意参赛的每两个队之间比赛一场,每个球队需要比赛场,x个队参赛需要参赛,但是两个球队不重复比赛,所以乘以,即可解得.
【解析】根据题意得:
,
故选:D.
【点睛】此题考查了一元二次方程解应用题,解题的关键是根据题意找出等量关系式.
6.3或6
【分析】延长交于点C,延长交于点D,可得四边形是矩形,依据与面积相等,线段将三个正方形分成面积相等的两部分,即可得到四边形与四边形的面积相等,进而得到x的值.
【解析】解:如图所示,延长交于点C,延长交于点D,则四边形是矩形,
∴与面积相等,
又∵线段将三个正方形分成面积相等的两部分,
∴四边形与四边形的面积相等,
∴,
解得或6,
故答案为:3或6.
【点睛】此题考查一元二次方程的实际应用,矩形的性质,正方形的性质,题中的辅助线的引入是难点.
7.10
【分析】本题可设原正方形的边长为,则剩余的空地长为,宽为.根据长方形的面积公式方程可列出,进而可求出原正方形的边长.
【解析】解:设原正方形的边长为,依题意得:
,
解得:,(不合题意,舍去),
故原正方形的边长.
故答案是:10.
【点睛】本题考查一元二次方程的应用.正确记忆长方形的面积公式,求得剩余的空地的长和宽是解决本题的关键.
8.2或4
【分析】由题意可知当运动时间为t秒时,则AP=t cm,BP=(6-t)cm,BQ=2t cm,CQ=(12-2t)cm,根据S△DPQ=28cm2,即可得出关于t的一元二次方程,解之即可得出答案.
【解析】解:当运动时间为t秒时,则AP=t cm,BP=(6-t)cm,BQ=2t cm,CQ=(12-2t)cm,
依题意得:12×6-×12t-×6(12-2t)-×2t (6-t)=28,
整理得:t2-6t+8=0,
解得:t1=2,t2=4.
故答案为:2或4.
【点睛】本题考查一元二次方程的几何应用与矩形的性质,找准等量关系,正确列出一元二次方程是解题的关键.
9.
【分析】根据,有,再根据,可得,即,解方程即可求解,问题随之得解.
【解析】∵,
∴,
∵,
∴,即,
解得:(负值舍去),
∵,
∴,
故答案为:.
【点睛】本题主要考查了一元二次方程的应用,根据题意得到关于的一元二次方程是解答本题的关键.
10.2
【分析】设这个盒子的高为x cm,则做成的无盖长方体的底面长为(20 2x)cm,宽为(10 2x)cm,根据无盖长方体盒子的底面积为,即可得出关于x的一元二次方程,解之即可得出x的值,再结合盒子的高为正值,即可解答.
【解析】解:设这个盒子的高为x cm,则做成的无盖长方体的底面长为cm,宽为cm,
依题意得:,
整理得:,
解得:,.
又∵,
∴,
∴,
故答案为:2.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
11.的值为
【分析】根据各边之间的关系,可得出的长为,根据矩形养殖场的面积为,可得出关于的一元二次方程,解之取其符合题意的值,即可得出结论.
【解析】解:∵栅栏总长度为,的长为,
∴的长为.
根据题意得:,整理得:,
解得:,,
当时,,不符合题意,舍去;
当时,,符合题意.
∴此时的值为.
【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
12.2m.
【分析】把所修的两条道路分别平移到矩形的最上边和最左边,则剩下的部分是一个长方形,根据长方形的面积公式列方程即可.
【解析】解:设道路的宽应为x米,剩余部分拼成一个长方形,长和宽分别为(12﹣x)米、(8﹣x)米,
由题意得,(12﹣x)(8﹣x)=60.
解得x=2或x=18(舍去).
答:道路的宽应设计为2m.
【点睛】此题主要考查了一元二次方程的应用,把中间修建的两条道路分别平移到矩形地面的最上边和最左边是做本题的关键.
13.
【分析】设切去的正方形的边长为,根据制作成一个底面积为的无盖方盒列出等量关系式即可解得.
【解析】解:设切去的正方形的边长为,
,(舍去)
答:去的正方形的边长为.
【点睛】此题考查了一元二次的方程的实际应用,解题的关键是根据题意列出等量关系式.
14.(1);
(2)能,第10个图中的棋子个数为115.
【分析】(1)先观察得出图形变化中的规律,再利用规律求解即可;
(2)令建立方程求解,检验n的值是否符合题意,即可求解.
【解析】(1)第1个图:,
第2个图:,
第3个图:,
…
第5个图:,
由图中规律可知,第个图:,
故答案为:;.
(2)令,
解得(舍去),,
∴能,第10个图中的棋子个数为115.
【点睛】本题考查了图形规律题,涉及到了一元二次方程的应用,解题关键是发现图中的变化规律,并能用数式进行表示.
15.(1)2s或4s;(2);(3)
【分析】(1)根据题意表示出BP,BQ,然后利用列出方程,解方程即可;
(2)根据勾股定理列出一个关于t的一元二次方程,解方程即可得出答案;
(3)首先根据勾股定理求出AC的长,作于点E,连接DB,则DE可求,进而利用勾股定理求出AE的长度,则可得出DE的长度,最后再利用勾股定理即可求解.
【解析】(1)根据题意有,
,
,
,
解得或,
∴当t为2s或4s时,的面积是;
(2)∵,
,
即,
解得或(舍去),
∴当时,点和点间的距离是;
(3)∵,
.
根据题意得,
解得,
∴.
作于点E,连接DB,
则 ,
,
,
.
【点睛】本题主要考查三角形中的动点问题,掌握勾股定理,一元二次方程的解法是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
