初中八年级下册浙教版 平行四边形 同步练习(含答案)
文档属性
| 名称 | 初中八年级下册浙教版 平行四边形 同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 61.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-03-27 00:00:00 | ||
图片预览



文档简介
平行四边形同步练习
◆知能点分类训练
知能点1 平行四边形的定义
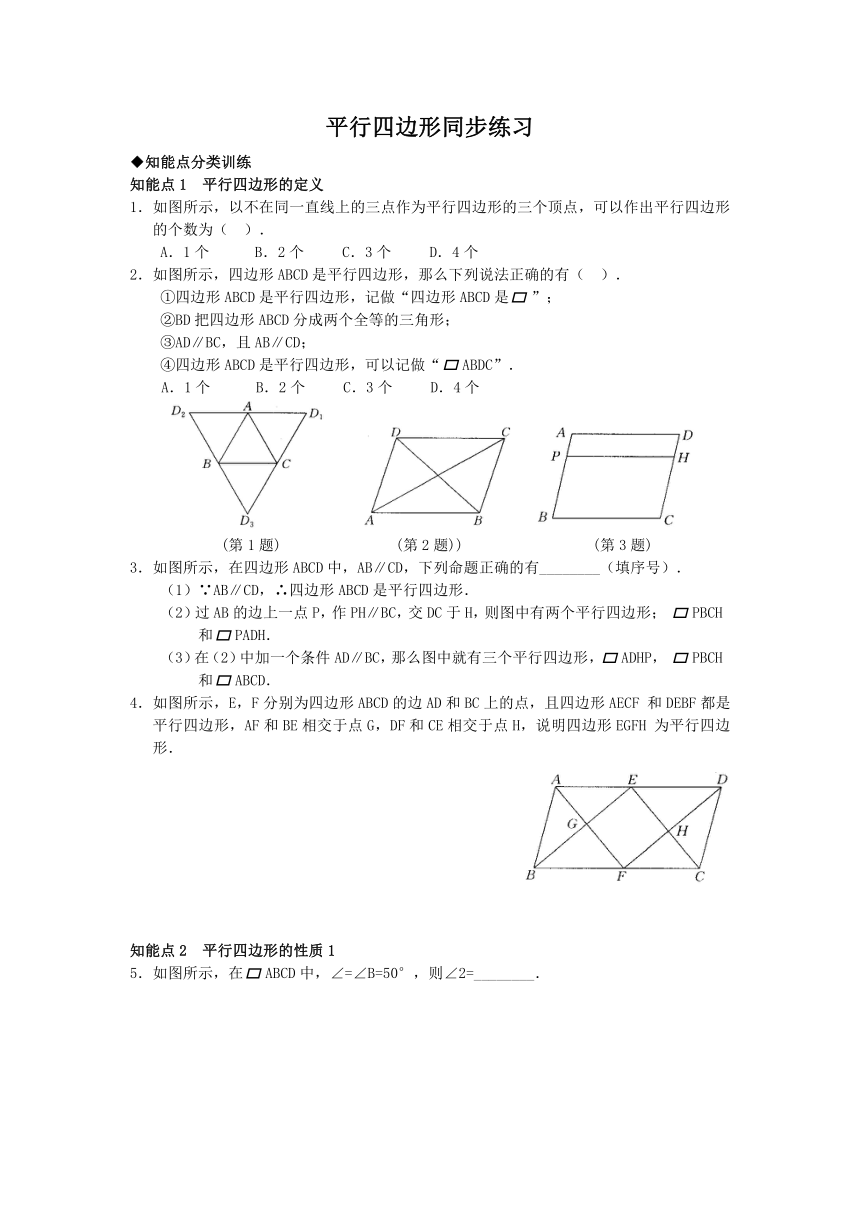
1.如图所示,以不在同一直线上的三点作为平行四边形的三个顶点,可以作出平行四边形的个数为( ).
A.1个 B.2个 C.3个 D.4个
2.如图所示,四边形ABCD是平行四边形,那么下列说法正确的有( ).
①四边形ABCD是平行四边形,记做“四边形ABCD是”;
②BD把四边形ABCD分成两个全等的三角形;
③AD∥BC,且AB∥CD;
④四边形ABCD是平行四边形,可以记做“ABDC”.
A.1个 B.2个 C.3个 D.4个
(第1题) (第2题)) (第3题)
3.如图所示,在四边形ABCD中,AB∥CD,下列命题正确的有________(填序号).
(1)∵AB∥CD,∴四边形ABCD是平行四边形.
(2)过AB的边上一点P,作PH∥BC,交DC于H,则图中有两个平行四边形;PBCH
和PADH.
(3)在(2)中加一个条件AD∥BC,那么图中就有三个平行四边形,ADHP,PBCH
和ABCD.
4.如图所示,E,F分别为四边形ABCD的边AD和BC上的点,且四边形AECF和DEBF都是平行四边形,AF和BE相交于点G,DF和CE相交于点H,说明四边形EGFH为平行四边形.
知能点2 平行四边形的性质1
5.如图所示,在ABCD中,∠=∠B=50°,则∠2=________.
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
(第5题) (第6题) (第8题)
6.如图所示,在ABCD中,AB=4cm,AD=7cm,∠ABC的平分线BF交AD于点E, 交CD的延长线于点F,则DF=________cm.
7.已知平行四边形的周长为28cm,相邻两边的差为4cm,求两边的长.
8.如图所示,在ABCD中,E,F分别是AC,CA的延长线上的点,且CE=AF.
求证:BF∥DE.
能点3 平行四边形的性质2
9.在ABCD中,∠B-∠A=30°,则∠A,∠B,∠C,∠D的度数是( ).
A.95°,85°,95°,85° B.85°,95°,85°,95°
C.105°,75°,105°,75° D.75°,105°,75°,105°
10.在ABCD中,若∠A:∠B=5:4,则∠C的度数为( ).
A.80° B.120° C.100° D.110°
11.在ABCD中,∠A:∠B:∠C:∠D的值可以是( ).
A.1:2:3:4 B.3:4:4:3 C.3:3:4:4 D.3:4:3:4
12.如图所示,在ABCD中,∠D-∠A=∠1=60°,AD=5cm,求EC的长.
◆规律方法应用
13.如图所示,在ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F,求证:BE=DF.
14.如图所示,已知点E为AC的中点,AG∥BC,GE∥AB,交BC于点F,求证:BF=FC.
15.如图所示,在ABCD中,∠ABC,∠ADC的平分线分别交对边于点E,F,交四边形的对角线AC于点G,H,求证:AH=CG.
16.如图所示,是某市部分街道示意图,AF∥BC,EC⊥BC,BA∥DE,BD∥AE.甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F;乙乘2路车,路线是B→D→C→F.假设两车速度相同,途中耽误时间相同,那么谁先到达F站?说明理由.
◆开放探索创新
17.如图所示,在ABCD中,AE,BE,CF,DF分别平分∠DAB,∠ABC,∠BCD,∠CDA,且AE,DF相交于点M,BE,CF相交于点N.在不添加其他条件的情况下,写出一个由上述条件推出的结论.(要求:给出推理过程)推理过程中,必须用“平行四边形”和“角平分线”的性质.
◆中考真题实战
18.(杭州)如下左图所示,在ABCD中,∠B=130°,延长AD到F,延长CD到E,连接EF,则∠E+∠F等于( ).
A.130° B.40° C.50° D.70°
19.如上右图所示,在平面直角坐标系中,ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( ).
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
20.如图所示,在ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD.
(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.
参考答案
1.C 2.B 3.(3)
4.解:∵四边形AECF为平行四边形,∴AF∥CE.
∵四边形DEBF为平行四边形,∴BE∥DF.
∴四边形EGFH为平行四边形.
5.80°
6.3 提示:利用平行四边形的性质.
7.解:设相邻两边长为xcm,ycm(x>y),
∵平行四边形的对边相等,∴2x+3y=28.
∴
∴相邻两边的长分别为9cm和5cm.
8.证明:∵四边形ABCD是平行四边形,
∴ABCD,∴∠1=∠2,∠3=∠4.
又∵AF=CE
∴在△ABF和△CDE中,有HYPERLINK "http://www.21cnjy.com" \o "欢迎登陆21世纪教育网"
∴△ABF≌△CDE,
∴∠F=∠E,
∴BF∥DE.
9.D 10.C 11.D
12.解:如答图所示,在ABCD中,
∵∠D+∠A=180°,∠D-∠A=60°.
∴∠D=120°,∠ABC=∠D=120°.
∵∠1=60°,
∴∠3=60°,且∠2=∠ABC-∠1=60°,
即∠2=∠3.
∴EC=BC=AD=5cm.
13.证明:∵四边形ABCD为平行四边形.
∴AB∥CD,AB=CD,∴∠ABE=∠CDF.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
∴Rt△ABE≌Rt△CDF(AAS).
∴BE=DF.
14.证明:∵AG∥BC,
∴∠C=∠GAE,∠EFG=∠G.
又∵E为AC的中点,∴AE=EC.
∴△AEG≌△CEF(AAS),∴AG=FC.
又∵AG∥BC,GE∥AB,
∴四边形ABFG为平行四边形.
∴AG=BF,∴BF=FC.
15.证明:∵四边形ABCD为平行四边形.
∴AD∥BC,AD=BC,∴∠ADC=∠ABC.
∵AD∥BC,∴∠DAC=∠BCA.
又∵DF,BE分别平分∠ADC,∠ABC,
∴∠ADF=∠ADC,∠CBE=∠ABC.
∴∠ADF=∠CBE,
∴△ADH≌△CBG(ASA),∴AH=CG.
16.解:过D作DG⊥BC于G,∴∠DGB=90°.
∵AE∥BD,BA∥DE,∴ABDE为平行四边形.
∴AE=BD,AB=DE,∠EAD=∠ADB.
又∵AF∥BC,∴∠ADB=∠DBC,∠EFA=∠FCB,∴∠EAD=∠DBC.
∵EC⊥BC,∴∠FCB=90°,∠EFA=90°.
∴∠EFA=∠DGB=∠FCB,EC⊥AF.
∴△EAF≌△DBG(AAS),DG∥FC,
∴EF=DG.
∵AF∥BC,DG∥FC,∴DG=FC,EF=FC.
∵EC⊥AF,∴∠DFE=∠DFC=90°.
又∵DF=DF,∴△DEF≌△DFC(SAS).
∴DE=DC,∴AB=DC.
∵甲的路线长=AB+AE+EF,
乙的路线长=BD+DC+CF.
∴甲的路线长=乙的路线长.
∵两人乘车速度相同,途中耽误时间相同.
∴甲、乙两人同时到达.
17.解:AE⊥BE.(仅举一例说明)
在ABCD中,∵AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE,BE分别平分∠DAB,∠ABC,
∴∠EAB+∠EBA=(∠DAB+∠ABC)=×180°=90°.
∴∠AEB=90°,∴AE⊥BE.
18.C 19.C
20.证明:(1)∵四边形ABCD为平行四边形.
∴AD∥BC,AD=BC,∴∠DAE=∠AEB.
∵AB=AE,∴∠AEB=∠B.
∴∠B=∠DAE,∴△ABC≌△EAD.
(2)∵∠DAE=∠BAE,∠DAE=∠AEB,
∴∠BAE=∠AEB=∠B,∴△ABE为等边三角形,∴∠BAE=60°.
∵∠EAC=25°,∴∠BAC=85°.
∵△ABC≌△EAD,∴∠AED=∠BAC=85°.
◆知能点分类训练
知能点1 平行四边形的定义
1.如图所示,以不在同一直线上的三点作为平行四边形的三个顶点,可以作出平行四边形的个数为( ).
A.1个 B.2个 C.3个 D.4个
2.如图所示,四边形ABCD是平行四边形,那么下列说法正确的有( ).
①四边形ABCD是平行四边形,记做“四边形ABCD是”;
②BD把四边形ABCD分成两个全等的三角形;
③AD∥BC,且AB∥CD;
④四边形ABCD是平行四边形,可以记做“ABDC”.
A.1个 B.2个 C.3个 D.4个
(第1题) (第2题)) (第3题)
3.如图所示,在四边形ABCD中,AB∥CD,下列命题正确的有________(填序号).
(1)∵AB∥CD,∴四边形ABCD是平行四边形.
(2)过AB的边上一点P,作PH∥BC,交DC于H,则图中有两个平行四边形;PBCH
和PADH.
(3)在(2)中加一个条件AD∥BC,那么图中就有三个平行四边形,ADHP,PBCH
和ABCD.
4.如图所示,E,F分别为四边形ABCD的边AD和BC上的点,且四边形AECF和DEBF都是平行四边形,AF和BE相交于点G,DF和CE相交于点H,说明四边形EGFH为平行四边形.
知能点2 平行四边形的性质1
5.如图所示,在ABCD中,∠=∠B=50°,则∠2=________.
( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )
(第5题) (第6题) (第8题)
6.如图所示,在ABCD中,AB=4cm,AD=7cm,∠ABC的平分线BF交AD于点E, 交CD的延长线于点F,则DF=________cm.
7.已知平行四边形的周长为28cm,相邻两边的差为4cm,求两边的长.
8.如图所示,在ABCD中,E,F分别是AC,CA的延长线上的点,且CE=AF.
求证:BF∥DE.
能点3 平行四边形的性质2
9.在ABCD中,∠B-∠A=30°,则∠A,∠B,∠C,∠D的度数是( ).
A.95°,85°,95°,85° B.85°,95°,85°,95°
C.105°,75°,105°,75° D.75°,105°,75°,105°
10.在ABCD中,若∠A:∠B=5:4,则∠C的度数为( ).
A.80° B.120° C.100° D.110°
11.在ABCD中,∠A:∠B:∠C:∠D的值可以是( ).
A.1:2:3:4 B.3:4:4:3 C.3:3:4:4 D.3:4:3:4
12.如图所示,在ABCD中,∠D-∠A=∠1=60°,AD=5cm,求EC的长.
◆规律方法应用
13.如图所示,在ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F,求证:BE=DF.
14.如图所示,已知点E为AC的中点,AG∥BC,GE∥AB,交BC于点F,求证:BF=FC.
15.如图所示,在ABCD中,∠ABC,∠ADC的平分线分别交对边于点E,F,交四边形的对角线AC于点G,H,求证:AH=CG.
16.如图所示,是某市部分街道示意图,AF∥BC,EC⊥BC,BA∥DE,BD∥AE.甲、乙两人同时从B站乘车到F站,甲乘1路车,路线是B→A→E→F;乙乘2路车,路线是B→D→C→F.假设两车速度相同,途中耽误时间相同,那么谁先到达F站?说明理由.
◆开放探索创新
17.如图所示,在ABCD中,AE,BE,CF,DF分别平分∠DAB,∠ABC,∠BCD,∠CDA,且AE,DF相交于点M,BE,CF相交于点N.在不添加其他条件的情况下,写出一个由上述条件推出的结论.(要求:给出推理过程)推理过程中,必须用“平行四边形”和“角平分线”的性质.
◆中考真题实战
18.(杭州)如下左图所示,在ABCD中,∠B=130°,延长AD到F,延长CD到E,连接EF,则∠E+∠F等于( ).
A.130° B.40° C.50° D.70°
19.如上右图所示,在平面直角坐标系中,ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是( ).
A.(3,7) B.(5,3) C.(7,3) D.(8,2)
20.如图所示,在ABCD中,E为BC边上一点,且AB=AE.
(1)求证:△ABC≌△EAD.
(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.
参考答案
1.C 2.B 3.(3)
4.解:∵四边形AECF为平行四边形,∴AF∥CE.
∵四边形DEBF为平行四边形,∴BE∥DF.
∴四边形EGFH为平行四边形.
5.80°
6.3 提示:利用平行四边形的性质.
7.解:设相邻两边长为xcm,ycm(x>y),
∵平行四边形的对边相等,∴2x+3y=28.
∴
∴相邻两边的长分别为9cm和5cm.
8.证明:∵四边形ABCD是平行四边形,
∴ABCD,∴∠1=∠2,∠3=∠4.
又∵AF=CE
∴在△ABF和△CDE中,有HYPERLINK "http://www.21cnjy.com" \o "欢迎登陆21世纪教育网"
∴△ABF≌△CDE,
∴∠F=∠E,
∴BF∥DE.
9.D 10.C 11.D
12.解:如答图所示,在ABCD中,
∵∠D+∠A=180°,∠D-∠A=60°.
∴∠D=120°,∠ABC=∠D=120°.
∵∠1=60°,
∴∠3=60°,且∠2=∠ABC-∠1=60°,
即∠2=∠3.
∴EC=BC=AD=5cm.
13.证明:∵四边形ABCD为平行四边形.
∴AB∥CD,AB=CD,∴∠ABE=∠CDF.
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°.
∴Rt△ABE≌Rt△CDF(AAS).
∴BE=DF.
14.证明:∵AG∥BC,
∴∠C=∠GAE,∠EFG=∠G.
又∵E为AC的中点,∴AE=EC.
∴△AEG≌△CEF(AAS),∴AG=FC.
又∵AG∥BC,GE∥AB,
∴四边形ABFG为平行四边形.
∴AG=BF,∴BF=FC.
15.证明:∵四边形ABCD为平行四边形.
∴AD∥BC,AD=BC,∴∠ADC=∠ABC.
∵AD∥BC,∴∠DAC=∠BCA.
又∵DF,BE分别平分∠ADC,∠ABC,
∴∠ADF=∠ADC,∠CBE=∠ABC.
∴∠ADF=∠CBE,
∴△ADH≌△CBG(ASA),∴AH=CG.
16.解:过D作DG⊥BC于G,∴∠DGB=90°.
∵AE∥BD,BA∥DE,∴ABDE为平行四边形.
∴AE=BD,AB=DE,∠EAD=∠ADB.
又∵AF∥BC,∴∠ADB=∠DBC,∠EFA=∠FCB,∴∠EAD=∠DBC.
∵EC⊥BC,∴∠FCB=90°,∠EFA=90°.
∴∠EFA=∠DGB=∠FCB,EC⊥AF.
∴△EAF≌△DBG(AAS),DG∥FC,
∴EF=DG.
∵AF∥BC,DG∥FC,∴DG=FC,EF=FC.
∵EC⊥AF,∴∠DFE=∠DFC=90°.
又∵DF=DF,∴△DEF≌△DFC(SAS).
∴DE=DC,∴AB=DC.
∵甲的路线长=AB+AE+EF,
乙的路线长=BD+DC+CF.
∴甲的路线长=乙的路线长.
∵两人乘车速度相同,途中耽误时间相同.
∴甲、乙两人同时到达.
17.解:AE⊥BE.(仅举一例说明)
在ABCD中,∵AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE,BE分别平分∠DAB,∠ABC,
∴∠EAB+∠EBA=(∠DAB+∠ABC)=×180°=90°.
∴∠AEB=90°,∴AE⊥BE.
18.C 19.C
20.证明:(1)∵四边形ABCD为平行四边形.
∴AD∥BC,AD=BC,∴∠DAE=∠AEB.
∵AB=AE,∴∠AEB=∠B.
∴∠B=∠DAE,∴△ABC≌△EAD.
(2)∵∠DAE=∠BAE,∠DAE=∠AEB,
∴∠BAE=∠AEB=∠B,∴△ABE为等边三角形,∴∠BAE=60°.
∵∠EAC=25°,∴∠BAC=85°.
∵△ABC≌△EAD,∴∠AED=∠BAC=85°.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
