浙教版2023年九年级下册第2章 《直线与圆的位置关系》单元检测卷(含解析)
文档属性
| 名称 | 浙教版2023年九年级下册第2章 《直线与圆的位置关系》单元检测卷(含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 631.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-21 09:05:50 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版2023年九年级下册第2章 《直线与圆的位置关系》单元检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)圆的半径是6.5cm,如果圆心与直线上某一点的距离是6.5cm,那么该直线和圆的位置关系是( )
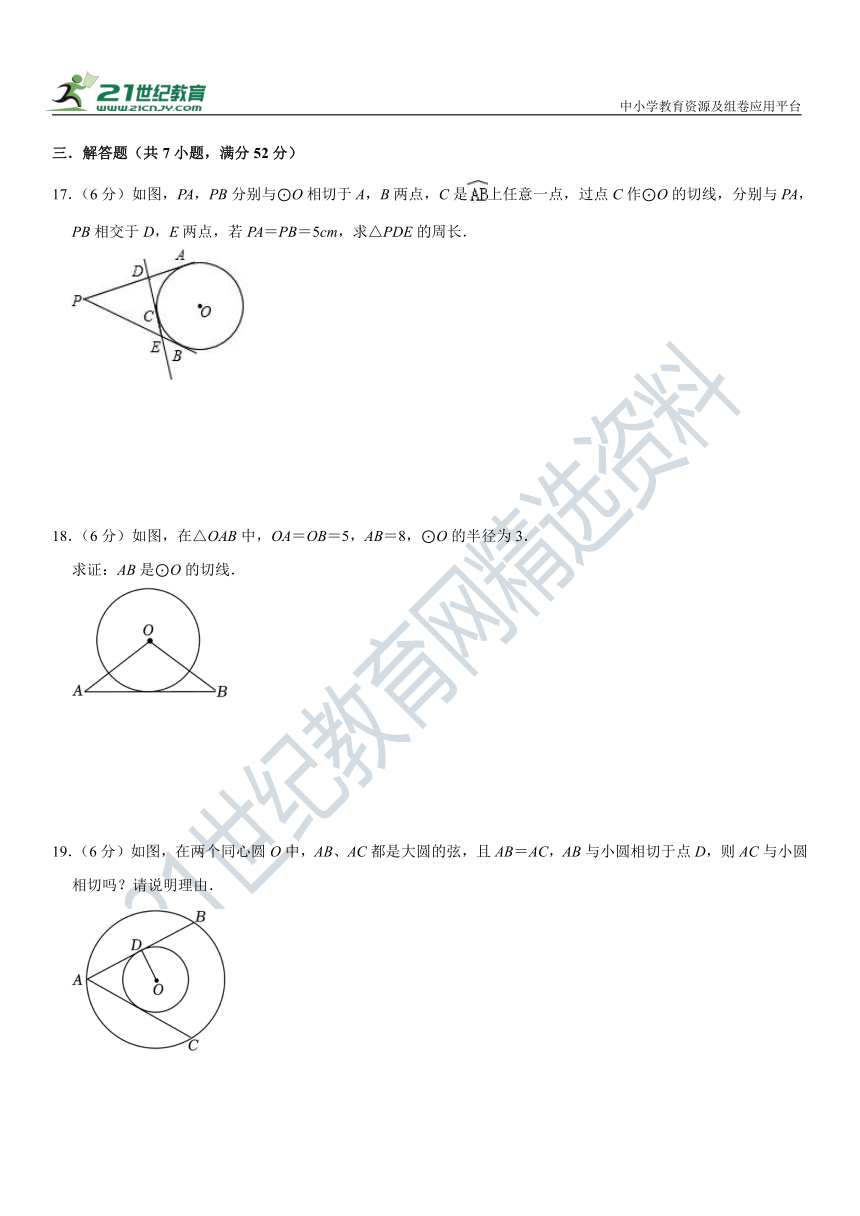
A.相离 B.相切 C.相交 D.相交或相切
2.(3分)已知⊙O的直径是6,直线l是⊙O的切线,则圆心O到直线l的距离是( )
A.3 B.4 C.6 D.12
3.(3分)如图,以点O为圆心作圆,所得的圆与直线a相切的是( )
A.以OA为半径的圆 B.以OB为半径的圆
C.以OC为半径的圆 D.以OD为半径的圆
4.(3分)如图,AB是⊙O的切线,B为切点,连接AO交⊙O于点C,延长AO交⊙O于点D,连接BD.若∠A=2∠D,且AB=2,则AC的长度是( )
A.1 B. C. D.
5.(3分)如图,AB是⊙O的直径,点C为⊙O上一点,过点C作⊙O的切线,交直径AB的延长线于点D,若∠ABC=65°,则∠D的度数是( )
A.25° B.30° C.40° D.50°
6.(3分)如图,⊙O内切于正方形ABCD,点O为圆心,作∠MON=90°,其两边分别交BC,CD于点M,N,交⊙O于点E,F,若CM+CN=6,则弧EF的长为( )
A.3π B.2.25π C.2π D.1.5π
7.(3分)如图,在△ABC中,∠ACB=90°,⊙O是△ABC的内切圆,三个切点分别为点D,E,F.若BF=2,AF=3,则△ABC的周长是( )
A.9 B. C.10 D.12
8.(3分)如图,PA、PB分别切⊙O于A、B,∠APB=60°,⊙O半径为3,则PA的长为( )
A.3 B.4 C.3 D.2
9.(3分)如图,在四边形ABCD中,AD∥BC,AB⊥BC,⊙O是四边形ABCD的内切圆,CD,BC分别切⊙O于F,E两点,若AD=3,BC=6,则EF的长是( )
A. B. C. D.
10.(3分)如图,直线AB、CD相交于点O,∠AOD=30°,半径为2cm的⊙P的圆心在直线AB上,且位于点O左侧的距离6cm处.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么( )秒钟后⊙P与直线CD相切.
A.2 B.10 C.2或10 D.6或8
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)直线l与⊙O相离,且⊙O的半径r等于3,圆心O到直线l的距离为d,则d的取值范围是 .
12.(3分)已知⊙O的圆心坐标为(3,0),直径为6,则⊙O与y轴的位置关系是 .
13.(3分)如图,⊙O是△ABC的内切圆,若∠A=50°,则∠BOC= .
14.(3分)如图,PA,PB是⊙O的切线,A,B是切点,若∠P=48°,则∠AOB= .
15.(3分)如图,四边形ABCD是⊙O的外切四边形,且AB=8,CD=15,则四边形ABCD的周长为 .
16.(3分)如图,点O是△PMN的内心,PO的延长线和△PMN的外接圆相交于点Q,连接NQ、MO、NO,若∠MNQ=15°,则∠MON的度数为 .
三.解答题(共7小题,满分52分)
17.(6分)如图,PA,PB分别与⊙O相切于A,B两点,C是上任意一点,过点C作⊙O的切线,分别与PA,PB相交于D,E两点,若PA=PB=5cm,求△PDE的周长.
18.(6分)如图,在△OAB中,OA=OB=5,AB=8,⊙O的半径为3.
求证:AB是⊙O的切线.
19.(6分)如图,在两个同心圆O中,AB、AC都是大圆的弦,且AB=AC,AB与小圆相切于点D,则AC与小圆相切吗?请说明理由.
20.(7分)如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,以点A为圆心,AB的长为半径作⊙A,直线BD与⊙A相切于点B,过点C作CD⊥BD于点D,交⊙A于点E.
(1)求∠CBD的度数.
(2)若⊙A的半径为5,求的长.
21.(8分)如图,在△ABC中,∠ACB=90°,点O为BC边上一点,以点O为圆心,OB长为半径的圆与边AB相交于点D,连接DC,且DC=AC.
(1)求证:CD是⊙O的切线;
(2)若DC=DB,⊙O的半径为1,求DC的长.
22.(9分)如图,AB为⊙O的直径,AC为弦,PC为⊙O的切线,C为切点,点E在⊙O上,AC=CE.连BE.
(1)求证:BE⊥PC;
(2)若AC=4,AB=2,求BE的长.
23.(10分)如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,连接CD交AB于点M.E是线段CM上的点,连接BE.F是△BDE的外接圆与AD的另一个交点,连接EF,BF.
(1)求证:△BEF是直角三角形;
(2)求证:△BEF∽△BCA;
(3)当AB=6,BC=m时,在线段CM上存在点E,使得EF和AB互相平分,求m的值.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:∵圆的半径为6.5cm,圆心与直线上某一点的距离是6.5cm,
∴圆的半径≥圆心到直线的距离,
∴直线于圆相切或相交,
故选:D.
2.【解答】解:由⊙O的直径是6,可知⊙O的半径是3,直线l是⊙O的切线,那么点O到直线l的距离是3.
故选:A.
3.【解答】解:∵OD⊥a于D,
∴以点O为圆心,OD为半径的圆与直线a相切.
故选:D.
4.【解答】解:如图,连接OB,
∵AB是⊙O的切线,B为切点,
∴OB⊥AB,
∴AB2=OA2﹣OB2,
∵OB和OD是半径,
∴∠D=∠OBD,
∵∠A=2∠D,
∴∠A=∠AOB,
∴AB=OB=OC=2,
∴OA==2,
∴AC=OA﹣OC=2﹣2.
故选:B.
5.【解答】解:连接OC,如图,
∵CD为切线,
∴OC⊥CD,
∴∠OCD=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=90°﹣∠ABC=90°﹣65°=25°,
∴∠BCD=∠A=25°,
∵∠OBC=∠BCD+∠D
∴∠D=65°﹣25°=40°.
故选:C.
6.【解答】解:设⊙O与正方形ABCD的边CD相切于点G,与BC相切于点H,如解图,连接OG,OH,则四边形OHCG是正方形,
∵∠GON+∠NOH=90°∠HOM+∠NOH=90°,
∴∠GON=∠HOM,
又∵∠OGN=∠OHM=90°,OG=OH,
∴△OGN≌△OHM(ASA),
∴GN=HM,
∴⊙O的半径=,
∴.
故选:D.
7.【解答】解:连接DO,EO,
∵⊙O是△ABC的内切圆,切点分别为D,E,F,
∴OE⊥AC,OD⊥BC,CD=CE,BD=BF=2,AF=AE=3,
∵∠C=90°,
∴四边形OECD是矩形,
∵EO=DO,
∴矩形OECD是正方形,
设EO=x,
则EC=CD=x,
在Rt△ABC中,BC2+AC2=AB2,
即(x+2)2+(x+3)2=52,
解得:x=1,
∴BC=3,AC=4,AB=5,
∴△ABC的周长为:3+4+5=12,
故选:D.
8.【解答】解:连接OA、OP,
∵PA、PB分别切⊙O于A、B,∠APB=60°,
∴∠APO=∠BPO=30°,OA⊥AP,
∴PA===3,
故选:C.
9.【解答】解:连接OC,与EF相交于点M,作DG⊥BC于点G,连接OE,设AD与圆的切点为H,如图,
∵AD∥BC,AB⊥BC,DG⊥BC,
∴四边形ABGD是矩形,
∴BG=AD=3,CG=BC﹣BG=6﹣3=3,
∵点E、F、H是切点,
∴DF=DH,CF=CE,OC平分∠ECF,
∴△ECF是等腰三角形,OC是EF的垂直平分线,
∴EM=FM,
设圆O半径为R,则BE=R,DG=2R,
∴CE=CF=6﹣R,DF=DH=3﹣R,
∵DG2+CG2=CD2,
∴(2R)2+32=[(3﹣R)+(6﹣R)]2,
解得:R=2,
∴CE=6﹣2=4,
∴,
∵,
∴,
∴,
故选:A.
10.【解答】解:由题意CD与圆P1相切于点E,点P在射线OA上,点P只能在直线CD的左侧.
∴P1E⊥CD,
又∵∠AOD=30°,r=2cm,
在△OEP1中OP1=4cm,
又∵OP=6cm,
∴P1P=2cm,
∴圆P到达圆P1需要时间为:2÷1=2(秒),
∴⊙P与直线CD相切时,时间为2秒,
当点P在点O的右侧时,同法可得t=10秒,
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
11.【解答】解:∵直线l与⊙O相离,⊙O的半径等于3,圆心O到直线l的距离为d,
∴d>3.
故答案为:d>3.
12.【解答】解:∵⊙O的圆心坐标为(3,0),
∴圆心O到y轴的距离为3,
∵⊙O的直径为6,
∴⊙O的半径为3,
∴圆心O到y轴的距离为等于⊙O的半径,
∴⊙O与y轴相切.
故答案为:相切.
13.【解答】解:∵∠A+∠ABC+∠ACB=180°,∠A=50°,
∴∠ABC+∠ACB=180°﹣∠A=130°,
∵⊙O是△ABC的内切圆,
∴∠ABO=∠CBO,∠ACO=∠BCO,
∴∠BCO=∠ACB,∠CBO=∠ABC,
∴∠BOC=180°﹣∠CBO﹣∠BCO=180°﹣∠ACB﹣∠ABC=180°﹣(∠ABC+∠ACB)=180°﹣×130°=115°,
故答案为:115°.
14.【解答】解:∵PA,PB是⊙O的切线,A,B是切点,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°,
∵∠OAP+∠AOB+∠OBP+∠P=360°,
∴∠AOB=360°﹣90°﹣90°﹣48°=132°.
故答案为:132°.
15.【解答】解:∵四边形ABCD是⊙O的外切四边形,如下图,
∴AE=AH,BE=BF,CF=CG,DH=DG,
∴AD+BC=AB+CD=23,
∴四边形ABCD的周长=AD+BC+AB+CD=23+23=46,
故答案为:46.
16.【解答】解:∵点O是△PMN的内心,
∴PQ平分∠MPN,
∴∠MPQ=∠NPQ,
∵∠MNQ=15°,
∴∠MPQ=∠NPQ=15°,
∴∠MPN=30°,
∴∠PMN+∠PNM=150°,
∵点O是△PMN的内心,
∴OM平分∠PMN,ON平分∠PNM,
∴∠OMN=PMN,∠PNM=PNM,
∴∠OMN+∠ONM=(∠PMN+∠PNM)=150°=75°,
∴∠MON=180°﹣(∠OMN+∠ONM)=105°,
故答案为:105°.
三.解答题(共7小题,满分52分)
17.【解答】解:∵PA与PB分别切⊙O于A、B两点,DE切⊙O于C,
∴DA=DC,EC=EB,
∵PA=PB=5cm,
∴△PDE的周长=PD+PE+DC+EC=PD+DA+PE+EB=PA+PB=10cm.
18.【解答】证明:如图,过O作OC⊥AB于C,
∵OA=OB,AB=8,
∴AC=AB=4,
在Rt△OAC中,OC===3,
∵⊙O的半径为3,
∴OC为⊙O的半径,
∴AB是⊙O的切线.
19.【解答】解:AC与小圆相切,理由如下:
过点O作OE⊥AC于E,设小圆与AB的切点为D,连接OD,OA,如图,
由切线性质可知OD⊥AB,
由垂径定理可知AE=EC,AD=DB,
∵AC=AB,
∴AE=AD,
在Rt△AEO和Rt△ADO中,
,
∴Rt△AEO≌Rt△ADO(HL),
∴OD=OE,
∴AC与小圆相切.
20.【解答】解:(1)∵∠BAC=120°,AB=AC,
∴∠ABC=∠ACB=30°,
∵直线BD与⊙A相切于点B,
∴∠ABD=90°,
∵CD⊥BD,
∴AB∥CD,
∴∠ABC=∠DCB=30°
∴∠CBD=90°﹣∠DCB=60°;
(2)连接AE,
∵∠CDB=90°,∠CBD=60°,
∴∠BCD=30°,
∴∠BAE=2∠BCE=60°,
∴的长为.
21.【解答】(1)证明:连接OD.
∵OD=OB,
∴∠ODB=∠B,
∵AC=DC,
∴∠CDA=∠A,
在△ABC中,∠ACB=90°,
∴∠A+∠B=90°,
∴∠CDA+∠ODB=90°,
∴∠ODC=180°﹣(∠CDA+ODB)=90°,即CD⊥OD,
∵OD是半径,
∴CD是⊙O的切线;
(2)解:连接DE,
∵BE是⊙O的的直径,
∴∠BDE=90°,
∴∠B+∠BED=90°,
∵OE=OD,
∴∠OED=∠ODE,
∵∠ODC=90°,即∠ODE+∠EDC=90°,
∴∠EDC=∠B,
∵OD=OB,
∴∠DOE=2∠B,
∵DB=DC,
∴∠B=∠ECD,
∴∠B=∠ECD=∠EDC,
∴∠OED=2∠ECD,
∵∠DOE=2∠B,
∴∠OED=∠DOE,
∴OD=DE=OE=1,
∴,
∴DC=DB=.
22.【解答】(1)证明:连接OC,OE,
∵AC=CE,OC=OC,OA=OE,
∴△AOC≌△EOC(SSS),
∴∠ACO=∠ECO,
∵AC=EC,
∴OC⊥AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴BE⊥AE,
∴BE∥OC,
∵PC切⊙O于C,
∴OC⊥PC,
∴BE⊥PC;
(2)解:连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴BC===2,
∵∠PCB+∠OCB=∠ACO+∠OCB=90°,
∴∠PCB=∠ACO,
∵∠CAO=∠ACO,
∴∠PCB=∠CAO,
∵∠P=∠P,
∴△PCB∽△PAC,
∴BC:AC=PC:PA=PB:PC=2:4=1:2,
令PC=x,则PA=2x,
∵PC2=PA PB,
∴x2=2x (2x﹣2),
∴x=,
∴PC=,
∵∠PCB=∠CAP,∠CAP=∠CEB,
∴∠PCB=∠CEB,
∵PC∥AE,
∴∠P=∠BAE,
∵∠ECB=∠BAE,
∴∠P=∠ECB,
∴△PCB∽△CEB,
∴CB:EB=PC:CE,
∴2:EB=:4,
∴EB=.
23.【解答】(1)证明:∵∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,
∴∠ADB=∠ACB=90°,
∵∠EFB=∠EDB,∠EBF=∠EDF,
∴∠EFB+∠EBF=∠EDB+∠EDF=∠ADB=90°,
∴∠BEF=90°,
∴△BEF是直角三角形.
(2)证明:∵BC=BD,
∴∠BDC=∠BCD,
∵∠EFB=∠EDB,
∴∠EFB=∠BCD,
∵AC=AD,BC=BD,
∴AB⊥CD,
∴∠AMC=90°,
∵∠BCD+∠ACD=∠ACD+∠CAB=90°,
∴∠BCD=∠CAB,
∴∠BFE=∠CAB,
∵∠ACB=∠FEB=90°,
∴△BEF∽△BCA.
(3)解:设EF交AB于J.连接AE.
∵EF与AB互相平分,
∴四边形AFBE是平行四边形,
∴∠EFA=∠FEB=90°,即EF⊥AD,
∵BD⊥AD,
∴EF∥BD,
∵AJ=JB,
∴AF=DF,
∴FJ=BD=,
∴EF=m,
∵△ABC∽△CBM,
∴BC:MB=AB:BC,
∴BM=,
∵△BEJ∽△BME,
∴BE:BM=BJ:BE,
∴BE=,
∵△BEF∽△BCA,
∴=,
即=,
解得m=2(负根已经舍弃).
浙教版2023年九年级下册第2章 《直线与圆的位置关系》单元检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)圆的半径是6.5cm,如果圆心与直线上某一点的距离是6.5cm,那么该直线和圆的位置关系是( )
A.相离 B.相切 C.相交 D.相交或相切
2.(3分)已知⊙O的直径是6,直线l是⊙O的切线,则圆心O到直线l的距离是( )
A.3 B.4 C.6 D.12
3.(3分)如图,以点O为圆心作圆,所得的圆与直线a相切的是( )
A.以OA为半径的圆 B.以OB为半径的圆
C.以OC为半径的圆 D.以OD为半径的圆
4.(3分)如图,AB是⊙O的切线,B为切点,连接AO交⊙O于点C,延长AO交⊙O于点D,连接BD.若∠A=2∠D,且AB=2,则AC的长度是( )
A.1 B. C. D.
5.(3分)如图,AB是⊙O的直径,点C为⊙O上一点,过点C作⊙O的切线,交直径AB的延长线于点D,若∠ABC=65°,则∠D的度数是( )
A.25° B.30° C.40° D.50°
6.(3分)如图,⊙O内切于正方形ABCD,点O为圆心,作∠MON=90°,其两边分别交BC,CD于点M,N,交⊙O于点E,F,若CM+CN=6,则弧EF的长为( )
A.3π B.2.25π C.2π D.1.5π
7.(3分)如图,在△ABC中,∠ACB=90°,⊙O是△ABC的内切圆,三个切点分别为点D,E,F.若BF=2,AF=3,则△ABC的周长是( )
A.9 B. C.10 D.12
8.(3分)如图,PA、PB分别切⊙O于A、B,∠APB=60°,⊙O半径为3,则PA的长为( )
A.3 B.4 C.3 D.2
9.(3分)如图,在四边形ABCD中,AD∥BC,AB⊥BC,⊙O是四边形ABCD的内切圆,CD,BC分别切⊙O于F,E两点,若AD=3,BC=6,则EF的长是( )
A. B. C. D.
10.(3分)如图,直线AB、CD相交于点O,∠AOD=30°,半径为2cm的⊙P的圆心在直线AB上,且位于点O左侧的距离6cm处.如果⊙P以1cm/s的速度沿由A向B的方向移动,那么( )秒钟后⊙P与直线CD相切.
A.2 B.10 C.2或10 D.6或8
二.填空题(共6小题,满分18分,每小题3分)
11.(3分)直线l与⊙O相离,且⊙O的半径r等于3,圆心O到直线l的距离为d,则d的取值范围是 .
12.(3分)已知⊙O的圆心坐标为(3,0),直径为6,则⊙O与y轴的位置关系是 .
13.(3分)如图,⊙O是△ABC的内切圆,若∠A=50°,则∠BOC= .
14.(3分)如图,PA,PB是⊙O的切线,A,B是切点,若∠P=48°,则∠AOB= .
15.(3分)如图,四边形ABCD是⊙O的外切四边形,且AB=8,CD=15,则四边形ABCD的周长为 .
16.(3分)如图,点O是△PMN的内心,PO的延长线和△PMN的外接圆相交于点Q,连接NQ、MO、NO,若∠MNQ=15°,则∠MON的度数为 .
三.解答题(共7小题,满分52分)
17.(6分)如图,PA,PB分别与⊙O相切于A,B两点,C是上任意一点,过点C作⊙O的切线,分别与PA,PB相交于D,E两点,若PA=PB=5cm,求△PDE的周长.
18.(6分)如图,在△OAB中,OA=OB=5,AB=8,⊙O的半径为3.
求证:AB是⊙O的切线.
19.(6分)如图,在两个同心圆O中,AB、AC都是大圆的弦,且AB=AC,AB与小圆相切于点D,则AC与小圆相切吗?请说明理由.
20.(7分)如图,在等腰三角形ABC中,AB=AC,∠BAC=120°,以点A为圆心,AB的长为半径作⊙A,直线BD与⊙A相切于点B,过点C作CD⊥BD于点D,交⊙A于点E.
(1)求∠CBD的度数.
(2)若⊙A的半径为5,求的长.
21.(8分)如图,在△ABC中,∠ACB=90°,点O为BC边上一点,以点O为圆心,OB长为半径的圆与边AB相交于点D,连接DC,且DC=AC.
(1)求证:CD是⊙O的切线;
(2)若DC=DB,⊙O的半径为1,求DC的长.
22.(9分)如图,AB为⊙O的直径,AC为弦,PC为⊙O的切线,C为切点,点E在⊙O上,AC=CE.连BE.
(1)求证:BE⊥PC;
(2)若AC=4,AB=2,求BE的长.
23.(10分)如图,在△ABC中,∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,连接CD交AB于点M.E是线段CM上的点,连接BE.F是△BDE的外接圆与AD的另一个交点,连接EF,BF.
(1)求证:△BEF是直角三角形;
(2)求证:△BEF∽△BCA;
(3)当AB=6,BC=m时,在线段CM上存在点E,使得EF和AB互相平分,求m的值.
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.【解答】解:∵圆的半径为6.5cm,圆心与直线上某一点的距离是6.5cm,
∴圆的半径≥圆心到直线的距离,
∴直线于圆相切或相交,
故选:D.
2.【解答】解:由⊙O的直径是6,可知⊙O的半径是3,直线l是⊙O的切线,那么点O到直线l的距离是3.
故选:A.
3.【解答】解:∵OD⊥a于D,
∴以点O为圆心,OD为半径的圆与直线a相切.
故选:D.
4.【解答】解:如图,连接OB,
∵AB是⊙O的切线,B为切点,
∴OB⊥AB,
∴AB2=OA2﹣OB2,
∵OB和OD是半径,
∴∠D=∠OBD,
∵∠A=2∠D,
∴∠A=∠AOB,
∴AB=OB=OC=2,
∴OA==2,
∴AC=OA﹣OC=2﹣2.
故选:B.
5.【解答】解:连接OC,如图,
∵CD为切线,
∴OC⊥CD,
∴∠OCD=90°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠A=90°﹣∠ABC=90°﹣65°=25°,
∴∠BCD=∠A=25°,
∵∠OBC=∠BCD+∠D
∴∠D=65°﹣25°=40°.
故选:C.
6.【解答】解:设⊙O与正方形ABCD的边CD相切于点G,与BC相切于点H,如解图,连接OG,OH,则四边形OHCG是正方形,
∵∠GON+∠NOH=90°∠HOM+∠NOH=90°,
∴∠GON=∠HOM,
又∵∠OGN=∠OHM=90°,OG=OH,
∴△OGN≌△OHM(ASA),
∴GN=HM,
∴⊙O的半径=,
∴.
故选:D.
7.【解答】解:连接DO,EO,
∵⊙O是△ABC的内切圆,切点分别为D,E,F,
∴OE⊥AC,OD⊥BC,CD=CE,BD=BF=2,AF=AE=3,
∵∠C=90°,
∴四边形OECD是矩形,
∵EO=DO,
∴矩形OECD是正方形,
设EO=x,
则EC=CD=x,
在Rt△ABC中,BC2+AC2=AB2,
即(x+2)2+(x+3)2=52,
解得:x=1,
∴BC=3,AC=4,AB=5,
∴△ABC的周长为:3+4+5=12,
故选:D.
8.【解答】解:连接OA、OP,
∵PA、PB分别切⊙O于A、B,∠APB=60°,
∴∠APO=∠BPO=30°,OA⊥AP,
∴PA===3,
故选:C.
9.【解答】解:连接OC,与EF相交于点M,作DG⊥BC于点G,连接OE,设AD与圆的切点为H,如图,
∵AD∥BC,AB⊥BC,DG⊥BC,
∴四边形ABGD是矩形,
∴BG=AD=3,CG=BC﹣BG=6﹣3=3,
∵点E、F、H是切点,
∴DF=DH,CF=CE,OC平分∠ECF,
∴△ECF是等腰三角形,OC是EF的垂直平分线,
∴EM=FM,
设圆O半径为R,则BE=R,DG=2R,
∴CE=CF=6﹣R,DF=DH=3﹣R,
∵DG2+CG2=CD2,
∴(2R)2+32=[(3﹣R)+(6﹣R)]2,
解得:R=2,
∴CE=6﹣2=4,
∴,
∵,
∴,
∴,
故选:A.
10.【解答】解:由题意CD与圆P1相切于点E,点P在射线OA上,点P只能在直线CD的左侧.
∴P1E⊥CD,
又∵∠AOD=30°,r=2cm,
在△OEP1中OP1=4cm,
又∵OP=6cm,
∴P1P=2cm,
∴圆P到达圆P1需要时间为:2÷1=2(秒),
∴⊙P与直线CD相切时,时间为2秒,
当点P在点O的右侧时,同法可得t=10秒,
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
11.【解答】解:∵直线l与⊙O相离,⊙O的半径等于3,圆心O到直线l的距离为d,
∴d>3.
故答案为:d>3.
12.【解答】解:∵⊙O的圆心坐标为(3,0),
∴圆心O到y轴的距离为3,
∵⊙O的直径为6,
∴⊙O的半径为3,
∴圆心O到y轴的距离为等于⊙O的半径,
∴⊙O与y轴相切.
故答案为:相切.
13.【解答】解:∵∠A+∠ABC+∠ACB=180°,∠A=50°,
∴∠ABC+∠ACB=180°﹣∠A=130°,
∵⊙O是△ABC的内切圆,
∴∠ABO=∠CBO,∠ACO=∠BCO,
∴∠BCO=∠ACB,∠CBO=∠ABC,
∴∠BOC=180°﹣∠CBO﹣∠BCO=180°﹣∠ACB﹣∠ABC=180°﹣(∠ABC+∠ACB)=180°﹣×130°=115°,
故答案为:115°.
14.【解答】解:∵PA,PB是⊙O的切线,A,B是切点,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°,
∵∠OAP+∠AOB+∠OBP+∠P=360°,
∴∠AOB=360°﹣90°﹣90°﹣48°=132°.
故答案为:132°.
15.【解答】解:∵四边形ABCD是⊙O的外切四边形,如下图,
∴AE=AH,BE=BF,CF=CG,DH=DG,
∴AD+BC=AB+CD=23,
∴四边形ABCD的周长=AD+BC+AB+CD=23+23=46,
故答案为:46.
16.【解答】解:∵点O是△PMN的内心,
∴PQ平分∠MPN,
∴∠MPQ=∠NPQ,
∵∠MNQ=15°,
∴∠MPQ=∠NPQ=15°,
∴∠MPN=30°,
∴∠PMN+∠PNM=150°,
∵点O是△PMN的内心,
∴OM平分∠PMN,ON平分∠PNM,
∴∠OMN=PMN,∠PNM=PNM,
∴∠OMN+∠ONM=(∠PMN+∠PNM)=150°=75°,
∴∠MON=180°﹣(∠OMN+∠ONM)=105°,
故答案为:105°.
三.解答题(共7小题,满分52分)
17.【解答】解:∵PA与PB分别切⊙O于A、B两点,DE切⊙O于C,
∴DA=DC,EC=EB,
∵PA=PB=5cm,
∴△PDE的周长=PD+PE+DC+EC=PD+DA+PE+EB=PA+PB=10cm.
18.【解答】证明:如图,过O作OC⊥AB于C,
∵OA=OB,AB=8,
∴AC=AB=4,
在Rt△OAC中,OC===3,
∵⊙O的半径为3,
∴OC为⊙O的半径,
∴AB是⊙O的切线.
19.【解答】解:AC与小圆相切,理由如下:
过点O作OE⊥AC于E,设小圆与AB的切点为D,连接OD,OA,如图,
由切线性质可知OD⊥AB,
由垂径定理可知AE=EC,AD=DB,
∵AC=AB,
∴AE=AD,
在Rt△AEO和Rt△ADO中,
,
∴Rt△AEO≌Rt△ADO(HL),
∴OD=OE,
∴AC与小圆相切.
20.【解答】解:(1)∵∠BAC=120°,AB=AC,
∴∠ABC=∠ACB=30°,
∵直线BD与⊙A相切于点B,
∴∠ABD=90°,
∵CD⊥BD,
∴AB∥CD,
∴∠ABC=∠DCB=30°
∴∠CBD=90°﹣∠DCB=60°;
(2)连接AE,
∵∠CDB=90°,∠CBD=60°,
∴∠BCD=30°,
∴∠BAE=2∠BCE=60°,
∴的长为.
21.【解答】(1)证明:连接OD.
∵OD=OB,
∴∠ODB=∠B,
∵AC=DC,
∴∠CDA=∠A,
在△ABC中,∠ACB=90°,
∴∠A+∠B=90°,
∴∠CDA+∠ODB=90°,
∴∠ODC=180°﹣(∠CDA+ODB)=90°,即CD⊥OD,
∵OD是半径,
∴CD是⊙O的切线;
(2)解:连接DE,
∵BE是⊙O的的直径,
∴∠BDE=90°,
∴∠B+∠BED=90°,
∵OE=OD,
∴∠OED=∠ODE,
∵∠ODC=90°,即∠ODE+∠EDC=90°,
∴∠EDC=∠B,
∵OD=OB,
∴∠DOE=2∠B,
∵DB=DC,
∴∠B=∠ECD,
∴∠B=∠ECD=∠EDC,
∴∠OED=2∠ECD,
∵∠DOE=2∠B,
∴∠OED=∠DOE,
∴OD=DE=OE=1,
∴,
∴DC=DB=.
22.【解答】(1)证明:连接OC,OE,
∵AC=CE,OC=OC,OA=OE,
∴△AOC≌△EOC(SSS),
∴∠ACO=∠ECO,
∵AC=EC,
∴OC⊥AE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴BE⊥AE,
∴BE∥OC,
∵PC切⊙O于C,
∴OC⊥PC,
∴BE⊥PC;
(2)解:连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴BC===2,
∵∠PCB+∠OCB=∠ACO+∠OCB=90°,
∴∠PCB=∠ACO,
∵∠CAO=∠ACO,
∴∠PCB=∠CAO,
∵∠P=∠P,
∴△PCB∽△PAC,
∴BC:AC=PC:PA=PB:PC=2:4=1:2,
令PC=x,则PA=2x,
∵PC2=PA PB,
∴x2=2x (2x﹣2),
∴x=,
∴PC=,
∵∠PCB=∠CAP,∠CAP=∠CEB,
∴∠PCB=∠CEB,
∵PC∥AE,
∴∠P=∠BAE,
∵∠ECB=∠BAE,
∴∠P=∠ECB,
∴△PCB∽△CEB,
∴CB:EB=PC:CE,
∴2:EB=:4,
∴EB=.
23.【解答】(1)证明:∵∠ACB=90°,将△ABC沿直线AB翻折得到△ABD,
∴∠ADB=∠ACB=90°,
∵∠EFB=∠EDB,∠EBF=∠EDF,
∴∠EFB+∠EBF=∠EDB+∠EDF=∠ADB=90°,
∴∠BEF=90°,
∴△BEF是直角三角形.
(2)证明:∵BC=BD,
∴∠BDC=∠BCD,
∵∠EFB=∠EDB,
∴∠EFB=∠BCD,
∵AC=AD,BC=BD,
∴AB⊥CD,
∴∠AMC=90°,
∵∠BCD+∠ACD=∠ACD+∠CAB=90°,
∴∠BCD=∠CAB,
∴∠BFE=∠CAB,
∵∠ACB=∠FEB=90°,
∴△BEF∽△BCA.
(3)解:设EF交AB于J.连接AE.
∵EF与AB互相平分,
∴四边形AFBE是平行四边形,
∴∠EFA=∠FEB=90°,即EF⊥AD,
∵BD⊥AD,
∴EF∥BD,
∵AJ=JB,
∴AF=DF,
∴FJ=BD=,
∴EF=m,
∵△ABC∽△CBM,
∴BC:MB=AB:BC,
∴BM=,
∵△BEJ∽△BME,
∴BE:BM=BJ:BE,
∴BE=,
∵△BEF∽△BCA,
∴=,
即=,
解得m=2(负根已经舍弃).
