2022-2023学年华东师大版数学九年级下册26.2.2 根据二次函数的图象判断式子的符号专题练习 (含解析)
文档属性
| 名称 | 2022-2023学年华东师大版数学九年级下册26.2.2 根据二次函数的图象判断式子的符号专题练习 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 11:36:51 | ||
图片预览




文档简介
根据二次函数的图象判断式子的符号专题测试卷(附解析)
学校:___________姓名:___________班级:___________考号:___________
满分120分 考试时间120分钟
一、单选题(每小题4分,共48分)
1.抛物线()的部分图像如图,则下列说法:①;②;③;④,正确的是( )
A.1个 B.2个 C.3个 D.4个
2.已知二次函数的图象如图所示,对称轴为.则下列结论中正确的是( )
A. B. C. D.
3.二次函数的图象如图所示,则下列结论:①;②一元二次方程的实数根为;③;④;⑤当时,.其中正确的结论是( )
A.①②③ B.②③④ C.③④⑤ D.①②④
4.已知二次函数的图象如图所示,则下列结论:①;②y随x的增大而增大;③方程两根之和大于零;④一次函数的图象一定不过第四象限,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
5.如图,抛物线的对称轴是直线,并与轴交于,两点,若,则下列结论中:;;;若为任意实数,则,正确的个数是( )
A. B. C. D.
6.如图,抛物线的对称轴是直线,并与x轴交于A,B两点,且,下列结论不正确的是( )
A. B.
C. D.若m为任意实数,则
7.二次函数的图象如图所示,在以下结论:①;②;③;④.其中正确的结论个数为( )
A.1 B.2 C.3 D.4
8.已知二次函数部分图象如图所示,图象过点,对称轴为直线,下列结论错误的是( )
A. B. C. D.
9.二次函数的对称轴是,图象如图所示,下面四个结论:①;②;③;④其中正确结论的个数是( )
A.4 B.3 C.2 D.1
10.二次函数的图象如图,给出下列四个结论:①;②;③;④,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
11.如图,抛物线的对称轴为直线,与轴的一个交点坐标为,其图象如图所示,下列结论:①;②方程的两个根为和3;③;④当时,x的取值范围是;⑤当时,y随x的增大而增大.其中错误的有( )个
A.4 B.3 C.2 D.1
12.抛物线交轴于,,交轴的负半轴于,顶点为下列结论:①;②;③当时,;④当是等腰直角三角形时,则;⑤当是等腰三角形时,的值有个.其中正确的有个( )
A. B. C. D.
二、填空题(每小题4分,共16分)
13.如下图,抛物线与x轴交于点下列判断:①;②;③;④.其中判断一定正确的序号是________.
14.如图,已知二次函数的图象与轴交于点,与轴的交点在和之间(不包括这两点),对称轴为直线.下列结论:①;②;③;④.其中正确结论有__________(填写所有正确结论的序号).
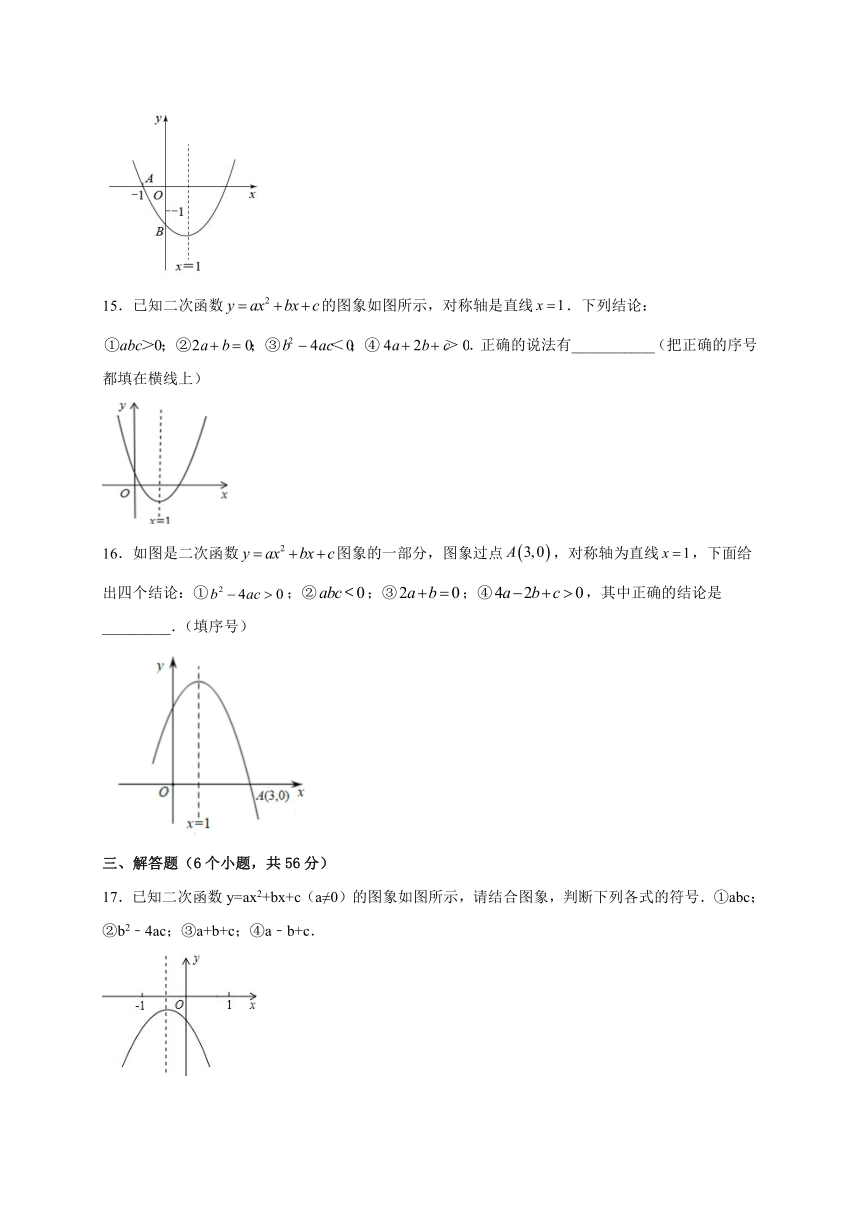
15.已知二次函数的图象如图所示,对称轴是直线.下列结论:.正确的说法有___________(把正确的序号都填在横线上)
16.如图是二次函数图象的一部分,图象过点,对称轴为直线,下面给出四个结论:①;②;③;④,其中正确的结论是_________.(填序号)
三、解答题(6个小题,共56分)
17.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,请结合图象,判断下列各式的符号.①abc;②b2﹣4ac;③a+b+c;④a﹣b+c.
18.如图,已知抛物线y=﹣x2+(m﹣1)x+m的对称轴为x=,请你解答下列问题:
(1)m= ,抛物线与x轴的交点为 .
(2)x取什么值时,y的值随x的增大而减小?
(3)x取什么值时,y<0?
19.抛物线的图象如图所示:
(1)判断,,,的符号;
(2)当时,求,,满足的关系.
20.已知抛物线,如图所示,直线是其对称轴,
确定,,,的符号;
求证:;
当取何值时,,当取何值时.
21.如图,抛物线C:经过点C(0,2),与x轴交于A,B两点.
(1)求此抛物线的解析式;
(2)点D(x1,y1),E(x2,y2)是抛物线C上两点,x1<2<x2,y1<0,y2>0.
①若∠CBD=75°,求BD所在直线的函数解析式;
②已知∠CBE=∠CBD,求证:(x1-1)(x2-1)为定值.
22.设二次函数y=ax2+bx+c(a>0,c>1),当x=c时,y=0;当0<x<c时,y>0.
(1)请比较ac和1的大小,并说明理由;
(2)当x>0时,求证:.
参考答案:
1.D
【详解】∵抛物线()的图像开口向上,
∴,
∵对称轴,
∴,
∴,
抛物线()的图像与轴交于,
∴,
∴,故①正确;
∵对称轴,
∴,
∴,故②正确;
∵抛物线()的图像与轴有两个交点,
∴,
∴,故③正确;
∵根据抛物线()的图像可知,
时,,
∴,故④正确;
故选:D
2.D
【详解】解:由抛物线的对称轴可得,故B错误;
由抛物线与轴的交点在轴的正半轴可得,
由抛物线的对称轴可得,则,故A错误;
由于抛物线与轴的左交点在到之间,根据抛物线的轴对称性可得:
抛物线与轴的右交点在5到6之间,
因而当时,,故C错误;
当时,,
由即可得,,则,故D正确.
故选:D.
3.D
【详解】解:∵抛物线的开口下,∴,
∵抛物线的对称轴为直线,
∴,
∵抛物线与y轴的正半轴相交,
∴,
∴,故①正确;
根据抛物线的对称性知,抛物线与x轴的交点坐标为和,
∴一元二次方程的实数根为,,故②正确;
∵,∴,故③错误;
由图象可知,当时,,故④正确;
由图象和②可知,当时,,故⑤错误,
综上,正确的结论是①②④,
故选:D.
4.C
【详解】∵当时,,对应的y值为正,即,故①正确;
∵因为抛物线开口向上,
∴在对称轴左侧,y随x的增大而减小;在对称轴右侧,y随x的增大而增大,故②错误;
∵由二次函数的图象可知:函数图象与x轴有两个不同的交点,即对应方程有两个不相等的实数根,且正根的绝对值较大,
∴方程两根之和大于零,故③正确;
∵由图象开口向上,知,与y轴交于负半轴,知,由对称轴,知,
∴,
∴一次函数的图象一定不经过第四象限,故④正确;
综上,正确的个数为3个,
故选:C.
5.C
【详解】解:观察图象可知:,,,
,故错误;
对称轴为直线,,
可得,,
点,点,
当时,,即,
,故正确;
抛物线的对称轴为直线,即,
,
,
,
,
,
,
,故正确;
当时,函数有最小值,
由,可得,
若为任意实数,则,故正确;
故选:C.
6.C
【详解】函数图像开口向下∴
对称轴为;;
又因为图像和y轴的交点在正半轴,∴
∴,故A正确,不符题意;
∵,∴,故B正确,不符题意;
∵,
∴,
∴
时,
故C错误,符合题意;
当时,函数取得最大值
当时,
由图像可知:
∴
故D正确,不符题意.
7.B
【详解】解:∵抛物线开口向上,则,
对称轴为直线,即,
∴,
∵抛物线与轴交于负半轴,则,
∴,故①不正确;
∵抛物线与轴有两个交点,
∴方程有两个不等实数根,
∴,即,故②正确;
∵,,
∴,故③不正确;
根据函数图象,当时,函数值小于0,即,
故④正确,
综上所述,②④正确,
故选:B.
8.C
【详解】解:A、∵抛物线开口向下,
∴,
∵对称轴为直线,即:,
∴,
∵抛物线与轴交于正半轴,
∴,
∴;选项正确,不符合题意;
B、当时,,
由A知:,
∴,选项正确,不符合题意;
C、抛物线关于直线对称,
∴的函数值等于的函数值,即:,选项错误,不符合题意;
D、抛物线关于直线对称,
∴的函数值等于的函数值,即:,
∵图象过,
∴,选项正确,不符合题意;
故选C.
9.B
【详解】解:由图象知,抛物线与x轴有两个交点,
∴方程有两个不相等的实数根,
∴,故①正确,
∵抛物线的对称轴直线为,
∴,
∴,
∴,故③正确,
由图象知,抛物线开口方向向下,
∴,
∵,
∴,而抛物线与y轴的交点在y轴的正半轴上,
∴,
∴,故②正确,
∵抛物线的对称轴直线为,
∴和时的函数值相等,
由图象可知此时抛物线在x轴下方,即,
∴,故④错误,
即正确的结论有3个,
故选:B.
10.B
【详解】解:①∵图像与轴有两个交点,
∴,
∴,
故①正确;
②∵当时,,
∴,
∴,
故②正确;
③∵图像的对称轴为,
∴,
∴,
∵由图像可知,当,,
∴,
∴,
∴,
∴,
∵抛物线的开口向下,
∴,
∴,
∴,
∴,
故③错误;
∵由可得:,
∴把代入可得,
∵,
∴,
∴,
∴或者,
即:只用当或时,才成立
故④错误.
故选.
11.B
【详解】解:抛物线与轴有2个交点,
,
,故①错误;
抛物线的对称轴为直线,
而点关于直线的对称点的坐标为,
方程的两个根是,,故②正确;
,即,
而时,,即,
,
即,故③错误;
抛物线与轴的两点坐标为,,
当时,的取值范围是,故④错误;
抛物线的对称轴为直线,
当时,随增大而增大,
当时,随增大而增大,故⑤正确;
所以其中结论正确有①③④,共3个.
故选:B.
12.C
【详解】解:抛物线交轴于,
抛物线对称轴为直线:
故①正确;
②∵交轴于,.
,
消去a得
故②错误;
∵抛物线开口向上,对称轴是
∴时,二次函数有最小值
∴时,
故③正确;
④∵,,是等腰直角三角形.
设点D坐标为.
则.
解得.
∵点D在x轴下方.
∴点D为.
设二次函数解析式为,过点.
∴.
解得.
故④正确;
⑤由题意可得,
,
.
故是等腰三角形时,只有两种情况,故a的值有2个.
故⑤错误.
故①③④正确,②⑤错误.
故选:C.
13.①②
【详解】解:∵抛物线开口向上,与y轴交于y轴负半轴,
∴,
∴,故①正确;
∵抛物线与x轴交于点,
∴,抛物线的对称轴为直线,
∴,,故②正确;
∴,
∴,故③错误;
∵当时,,
∴,故④错误;
∴正确的有①②;
故答案为:①②.
14.①③④
【详解】解:①函数开口方向向上,
;
对称轴在轴右侧
异号,
抛物线与轴交点在轴负半轴,
,
,故①正确;
②图象与轴交于点,对称轴为直线,
图象与轴的另一个交点为,
当时,,
,故②错误;
③二次函数的图象与轴的交点在的下方,对称轴在轴右侧,
最小值:,
,
;③正确;
④图象与轴的交点在和之间,
∵,
∴,
,
;故④正确;
综上所述,正确的有①③④,
故答案为:①③④.
15.②④.
【详解】解∶①抛物线开口方向向上,则.抛物线与轴交于正半轴,则,
所以,
故①错误;
②如图所示,对称轴,则,则,故②正确;
③如图所示,抛物线与轴有2个交点,则,故③错误;
④对称轴,当与时的点是关于直线的对应点,所以与时的函数值相等,所以,故④正确;综上所述,正确的结论为②④.
故答案为∶②④.
16.①②③
【详解】解:①由图象得,图象与x轴的一个交点为,对称轴为,
∴另一个交点为
∴方程有两个不相等的实数根,,正确;
②因为开口向下,故,
∵,
∴,
又,
∴,正确;
③由对称轴,得,正确;
④由①得另一个交点为,
∴时,,
当时,,即,故错误;
故①②③正确.
故答案为:①②③.
17.①abc<0;②b2﹣4ac<0;③a+b+c<0;④a﹣b+c<0
【详解】解:①抛物线开口向下,则a<0,对称轴在y轴的左侧,则x=﹣<0,则b<0,抛物线与y轴的交点在x轴的下方,则c<0,abc<0;
②抛物线与x轴没有交点,所以=b2﹣4ac<0;
③当自变量为1时,图象在x轴下方,则x=1时,y=a+b+c<0;
④当自变量为﹣1时,图象在x轴下方,则x=﹣1时,y=a﹣b+c<0.
18.(1)2;(﹣1,0),(2,0);(2)x>;(3)x<﹣1或x>2
【详解】解:(1)抛物线的对称轴为直线x= =,
∴m=2,
抛物线解析式为y=﹣x2+x+2,
当y=0时,﹣x2+x+2=0,
解得x1=﹣1,x2=2,
∴抛物线与x轴的交点为(﹣1,0),(2,0);
(2)由函数图象可知,
当x>时,y的值随x的增大而减小;
(3)由函数图象可知,
当x<﹣1或x>2时,y<0.
19.(1);(2).
【详解】(1)由图象可知,抛物线开口向下,可得:a<0;
x=0时,y=c>0;
∵对称轴x=,a<0,∴b>0;
图象与x轴有两个不同交点可得b2﹣4ac>0;
(2)当|OA|=|OB|时,即A点坐标为(﹣c,0),代入抛物线方程得y=ac2﹣bc+c两边同时除以c得:ac﹣b+1=0.
20.(1),,,;(2)详见解析;(3)当时,;当或时,.
【详解】∵抛物线开口向下,
∴,
∵对称轴,
∴,
∵抛物线与轴的交点在轴的上方,
∴,
∵抛物线与轴有两个交点,
∴;
证明:∵抛物线的顶点在轴上方,对称轴为,
∴当时,;
根据图象可知,
当时,;当或时,.
21.(1);(2)①;②见解析
【详解】(1)
∵经过点C(0,2),
∴把(0,2)代入得,
,
解得,
∴抛物线的解析式为,
(2)
①延长BD交y轴于点N,如图
∵令
∴,
∴A(1,0),B(2,0),
∴OC=OB=2,
∴,
∵∠CBD=75°,
∴∠OBD=30°,
∴在中,
∴,,
∴N(0,),
设BD所在直线的函数解析式为,
把B(2,0),N(0,)代入得,
∴,
∴BD所在直线的函数解析式为
②过点C作与BE的延长线相交于点P,
∵,CB=CB,,
∴CN=CP,
设直线BN的解析式为
直线BP的解析式为
将B(2,0)分别代入解析式中得,
∴直线BN的解析式为直线BP的解析式为
当时,
∴CN=2-(-2m)=2+2m,
∴CP=CN=2+2m,
∴P(2+2m,2),
将P(2+2m,2)代入解析式中得,
∴mn=1,
∵
∴可得
∵,
∴,
∴,
∴,
∴
∴为定值.
22.(1)ac≤1,理由见解析;(2)见解析
【详解】(1)解:当x=c时,y=0,即ac2+bc+c=0,c(ac+b+1)=0,
又c>1,所以ac+b+1=0
又因为当0<x<c时,y>0,x=c时,y=0,
于是二次函数y=ax2+bx+c的对称轴:即b≤﹣2ac
所以b=﹣ac﹣1≤﹣2ac即ac≤1;
(2)证明:因为0<x=1<c时,y>0,所以a+b+c>0
由ac≤1及a>0,c>1得:0<a<1
因为
=
而a+b+c>0,0<a<1,c>1,a﹣2ac﹣2+3c=(1﹣a)(2c﹣1)+(c﹣1)>0
所以当x>0时,,
即.
学校:___________姓名:___________班级:___________考号:___________
满分120分 考试时间120分钟
一、单选题(每小题4分,共48分)
1.抛物线()的部分图像如图,则下列说法:①;②;③;④,正确的是( )
A.1个 B.2个 C.3个 D.4个
2.已知二次函数的图象如图所示,对称轴为.则下列结论中正确的是( )
A. B. C. D.
3.二次函数的图象如图所示,则下列结论:①;②一元二次方程的实数根为;③;④;⑤当时,.其中正确的结论是( )
A.①②③ B.②③④ C.③④⑤ D.①②④
4.已知二次函数的图象如图所示,则下列结论:①;②y随x的增大而增大;③方程两根之和大于零;④一次函数的图象一定不过第四象限,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
5.如图,抛物线的对称轴是直线,并与轴交于,两点,若,则下列结论中:;;;若为任意实数,则,正确的个数是( )
A. B. C. D.
6.如图,抛物线的对称轴是直线,并与x轴交于A,B两点,且,下列结论不正确的是( )
A. B.
C. D.若m为任意实数,则
7.二次函数的图象如图所示,在以下结论:①;②;③;④.其中正确的结论个数为( )
A.1 B.2 C.3 D.4
8.已知二次函数部分图象如图所示,图象过点,对称轴为直线,下列结论错误的是( )
A. B. C. D.
9.二次函数的对称轴是,图象如图所示,下面四个结论:①;②;③;④其中正确结论的个数是( )
A.4 B.3 C.2 D.1
10.二次函数的图象如图,给出下列四个结论:①;②;③;④,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
11.如图,抛物线的对称轴为直线,与轴的一个交点坐标为,其图象如图所示,下列结论:①;②方程的两个根为和3;③;④当时,x的取值范围是;⑤当时,y随x的增大而增大.其中错误的有( )个
A.4 B.3 C.2 D.1
12.抛物线交轴于,,交轴的负半轴于,顶点为下列结论:①;②;③当时,;④当是等腰直角三角形时,则;⑤当是等腰三角形时,的值有个.其中正确的有个( )
A. B. C. D.
二、填空题(每小题4分,共16分)
13.如下图,抛物线与x轴交于点下列判断:①;②;③;④.其中判断一定正确的序号是________.
14.如图,已知二次函数的图象与轴交于点,与轴的交点在和之间(不包括这两点),对称轴为直线.下列结论:①;②;③;④.其中正确结论有__________(填写所有正确结论的序号).
15.已知二次函数的图象如图所示,对称轴是直线.下列结论:.正确的说法有___________(把正确的序号都填在横线上)
16.如图是二次函数图象的一部分,图象过点,对称轴为直线,下面给出四个结论:①;②;③;④,其中正确的结论是_________.(填序号)
三、解答题(6个小题,共56分)
17.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,请结合图象,判断下列各式的符号.①abc;②b2﹣4ac;③a+b+c;④a﹣b+c.
18.如图,已知抛物线y=﹣x2+(m﹣1)x+m的对称轴为x=,请你解答下列问题:
(1)m= ,抛物线与x轴的交点为 .
(2)x取什么值时,y的值随x的增大而减小?
(3)x取什么值时,y<0?
19.抛物线的图象如图所示:
(1)判断,,,的符号;
(2)当时,求,,满足的关系.
20.已知抛物线,如图所示,直线是其对称轴,
确定,,,的符号;
求证:;
当取何值时,,当取何值时.
21.如图,抛物线C:经过点C(0,2),与x轴交于A,B两点.
(1)求此抛物线的解析式;
(2)点D(x1,y1),E(x2,y2)是抛物线C上两点,x1<2<x2,y1<0,y2>0.
①若∠CBD=75°,求BD所在直线的函数解析式;
②已知∠CBE=∠CBD,求证:(x1-1)(x2-1)为定值.
22.设二次函数y=ax2+bx+c(a>0,c>1),当x=c时,y=0;当0<x<c时,y>0.
(1)请比较ac和1的大小,并说明理由;
(2)当x>0时,求证:.
参考答案:
1.D
【详解】∵抛物线()的图像开口向上,
∴,
∵对称轴,
∴,
∴,
抛物线()的图像与轴交于,
∴,
∴,故①正确;
∵对称轴,
∴,
∴,故②正确;
∵抛物线()的图像与轴有两个交点,
∴,
∴,故③正确;
∵根据抛物线()的图像可知,
时,,
∴,故④正确;
故选:D
2.D
【详解】解:由抛物线的对称轴可得,故B错误;
由抛物线与轴的交点在轴的正半轴可得,
由抛物线的对称轴可得,则,故A错误;
由于抛物线与轴的左交点在到之间,根据抛物线的轴对称性可得:
抛物线与轴的右交点在5到6之间,
因而当时,,故C错误;
当时,,
由即可得,,则,故D正确.
故选:D.
3.D
【详解】解:∵抛物线的开口下,∴,
∵抛物线的对称轴为直线,
∴,
∵抛物线与y轴的正半轴相交,
∴,
∴,故①正确;
根据抛物线的对称性知,抛物线与x轴的交点坐标为和,
∴一元二次方程的实数根为,,故②正确;
∵,∴,故③错误;
由图象可知,当时,,故④正确;
由图象和②可知,当时,,故⑤错误,
综上,正确的结论是①②④,
故选:D.
4.C
【详解】∵当时,,对应的y值为正,即,故①正确;
∵因为抛物线开口向上,
∴在对称轴左侧,y随x的增大而减小;在对称轴右侧,y随x的增大而增大,故②错误;
∵由二次函数的图象可知:函数图象与x轴有两个不同的交点,即对应方程有两个不相等的实数根,且正根的绝对值较大,
∴方程两根之和大于零,故③正确;
∵由图象开口向上,知,与y轴交于负半轴,知,由对称轴,知,
∴,
∴一次函数的图象一定不经过第四象限,故④正确;
综上,正确的个数为3个,
故选:C.
5.C
【详解】解:观察图象可知:,,,
,故错误;
对称轴为直线,,
可得,,
点,点,
当时,,即,
,故正确;
抛物线的对称轴为直线,即,
,
,
,
,
,
,
,故正确;
当时,函数有最小值,
由,可得,
若为任意实数,则,故正确;
故选:C.
6.C
【详解】函数图像开口向下∴
对称轴为;;
又因为图像和y轴的交点在正半轴,∴
∴,故A正确,不符题意;
∵,∴,故B正确,不符题意;
∵,
∴,
∴
时,
故C错误,符合题意;
当时,函数取得最大值
当时,
由图像可知:
∴
故D正确,不符题意.
7.B
【详解】解:∵抛物线开口向上,则,
对称轴为直线,即,
∴,
∵抛物线与轴交于负半轴,则,
∴,故①不正确;
∵抛物线与轴有两个交点,
∴方程有两个不等实数根,
∴,即,故②正确;
∵,,
∴,故③不正确;
根据函数图象,当时,函数值小于0,即,
故④正确,
综上所述,②④正确,
故选:B.
8.C
【详解】解:A、∵抛物线开口向下,
∴,
∵对称轴为直线,即:,
∴,
∵抛物线与轴交于正半轴,
∴,
∴;选项正确,不符合题意;
B、当时,,
由A知:,
∴,选项正确,不符合题意;
C、抛物线关于直线对称,
∴的函数值等于的函数值,即:,选项错误,不符合题意;
D、抛物线关于直线对称,
∴的函数值等于的函数值,即:,
∵图象过,
∴,选项正确,不符合题意;
故选C.
9.B
【详解】解:由图象知,抛物线与x轴有两个交点,
∴方程有两个不相等的实数根,
∴,故①正确,
∵抛物线的对称轴直线为,
∴,
∴,
∴,故③正确,
由图象知,抛物线开口方向向下,
∴,
∵,
∴,而抛物线与y轴的交点在y轴的正半轴上,
∴,
∴,故②正确,
∵抛物线的对称轴直线为,
∴和时的函数值相等,
由图象可知此时抛物线在x轴下方,即,
∴,故④错误,
即正确的结论有3个,
故选:B.
10.B
【详解】解:①∵图像与轴有两个交点,
∴,
∴,
故①正确;
②∵当时,,
∴,
∴,
故②正确;
③∵图像的对称轴为,
∴,
∴,
∵由图像可知,当,,
∴,
∴,
∴,
∴,
∵抛物线的开口向下,
∴,
∴,
∴,
∴,
故③错误;
∵由可得:,
∴把代入可得,
∵,
∴,
∴,
∴或者,
即:只用当或时,才成立
故④错误.
故选.
11.B
【详解】解:抛物线与轴有2个交点,
,
,故①错误;
抛物线的对称轴为直线,
而点关于直线的对称点的坐标为,
方程的两个根是,,故②正确;
,即,
而时,,即,
,
即,故③错误;
抛物线与轴的两点坐标为,,
当时,的取值范围是,故④错误;
抛物线的对称轴为直线,
当时,随增大而增大,
当时,随增大而增大,故⑤正确;
所以其中结论正确有①③④,共3个.
故选:B.
12.C
【详解】解:抛物线交轴于,
抛物线对称轴为直线:
故①正确;
②∵交轴于,.
,
消去a得
故②错误;
∵抛物线开口向上,对称轴是
∴时,二次函数有最小值
∴时,
故③正确;
④∵,,是等腰直角三角形.
设点D坐标为.
则.
解得.
∵点D在x轴下方.
∴点D为.
设二次函数解析式为,过点.
∴.
解得.
故④正确;
⑤由题意可得,
,
.
故是等腰三角形时,只有两种情况,故a的值有2个.
故⑤错误.
故①③④正确,②⑤错误.
故选:C.
13.①②
【详解】解:∵抛物线开口向上,与y轴交于y轴负半轴,
∴,
∴,故①正确;
∵抛物线与x轴交于点,
∴,抛物线的对称轴为直线,
∴,,故②正确;
∴,
∴,故③错误;
∵当时,,
∴,故④错误;
∴正确的有①②;
故答案为:①②.
14.①③④
【详解】解:①函数开口方向向上,
;
对称轴在轴右侧
异号,
抛物线与轴交点在轴负半轴,
,
,故①正确;
②图象与轴交于点,对称轴为直线,
图象与轴的另一个交点为,
当时,,
,故②错误;
③二次函数的图象与轴的交点在的下方,对称轴在轴右侧,
最小值:,
,
;③正确;
④图象与轴的交点在和之间,
∵,
∴,
,
;故④正确;
综上所述,正确的有①③④,
故答案为:①③④.
15.②④.
【详解】解∶①抛物线开口方向向上,则.抛物线与轴交于正半轴,则,
所以,
故①错误;
②如图所示,对称轴,则,则,故②正确;
③如图所示,抛物线与轴有2个交点,则,故③错误;
④对称轴,当与时的点是关于直线的对应点,所以与时的函数值相等,所以,故④正确;综上所述,正确的结论为②④.
故答案为∶②④.
16.①②③
【详解】解:①由图象得,图象与x轴的一个交点为,对称轴为,
∴另一个交点为
∴方程有两个不相等的实数根,,正确;
②因为开口向下,故,
∵,
∴,
又,
∴,正确;
③由对称轴,得,正确;
④由①得另一个交点为,
∴时,,
当时,,即,故错误;
故①②③正确.
故答案为:①②③.
17.①abc<0;②b2﹣4ac<0;③a+b+c<0;④a﹣b+c<0
【详解】解:①抛物线开口向下,则a<0,对称轴在y轴的左侧,则x=﹣<0,则b<0,抛物线与y轴的交点在x轴的下方,则c<0,abc<0;
②抛物线与x轴没有交点,所以=b2﹣4ac<0;
③当自变量为1时,图象在x轴下方,则x=1时,y=a+b+c<0;
④当自变量为﹣1时,图象在x轴下方,则x=﹣1时,y=a﹣b+c<0.
18.(1)2;(﹣1,0),(2,0);(2)x>;(3)x<﹣1或x>2
【详解】解:(1)抛物线的对称轴为直线x= =,
∴m=2,
抛物线解析式为y=﹣x2+x+2,
当y=0时,﹣x2+x+2=0,
解得x1=﹣1,x2=2,
∴抛物线与x轴的交点为(﹣1,0),(2,0);
(2)由函数图象可知,
当x>时,y的值随x的增大而减小;
(3)由函数图象可知,
当x<﹣1或x>2时,y<0.
19.(1);(2).
【详解】(1)由图象可知,抛物线开口向下,可得:a<0;
x=0时,y=c>0;
∵对称轴x=,a<0,∴b>0;
图象与x轴有两个不同交点可得b2﹣4ac>0;
(2)当|OA|=|OB|时,即A点坐标为(﹣c,0),代入抛物线方程得y=ac2﹣bc+c两边同时除以c得:ac﹣b+1=0.
20.(1),,,;(2)详见解析;(3)当时,;当或时,.
【详解】∵抛物线开口向下,
∴,
∵对称轴,
∴,
∵抛物线与轴的交点在轴的上方,
∴,
∵抛物线与轴有两个交点,
∴;
证明:∵抛物线的顶点在轴上方,对称轴为,
∴当时,;
根据图象可知,
当时,;当或时,.
21.(1);(2)①;②见解析
【详解】(1)
∵经过点C(0,2),
∴把(0,2)代入得,
,
解得,
∴抛物线的解析式为,
(2)
①延长BD交y轴于点N,如图
∵令
∴,
∴A(1,0),B(2,0),
∴OC=OB=2,
∴,
∵∠CBD=75°,
∴∠OBD=30°,
∴在中,
∴,,
∴N(0,),
设BD所在直线的函数解析式为,
把B(2,0),N(0,)代入得,
∴,
∴BD所在直线的函数解析式为
②过点C作与BE的延长线相交于点P,
∵,CB=CB,,
∴CN=CP,
设直线BN的解析式为
直线BP的解析式为
将B(2,0)分别代入解析式中得,
∴直线BN的解析式为直线BP的解析式为
当时,
∴CN=2-(-2m)=2+2m,
∴CP=CN=2+2m,
∴P(2+2m,2),
将P(2+2m,2)代入解析式中得,
∴mn=1,
∵
∴可得
∵,
∴,
∴,
∴,
∴
∴为定值.
22.(1)ac≤1,理由见解析;(2)见解析
【详解】(1)解:当x=c时,y=0,即ac2+bc+c=0,c(ac+b+1)=0,
又c>1,所以ac+b+1=0
又因为当0<x<c时,y>0,x=c时,y=0,
于是二次函数y=ax2+bx+c的对称轴:即b≤﹣2ac
所以b=﹣ac﹣1≤﹣2ac即ac≤1;
(2)证明:因为0<x=1<c时,y>0,所以a+b+c>0
由ac≤1及a>0,c>1得:0<a<1
因为
=
而a+b+c>0,0<a<1,c>1,a﹣2ac﹣2+3c=(1﹣a)(2c﹣1)+(c﹣1)>0
所以当x>0时,,
即.
