浙教版数学 八年级下第3章数据分析初步 教案
文档属性
| 名称 | 浙教版数学 八年级下第3章数据分析初步 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 135.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 19:16:14 | ||
图片预览



文档简介
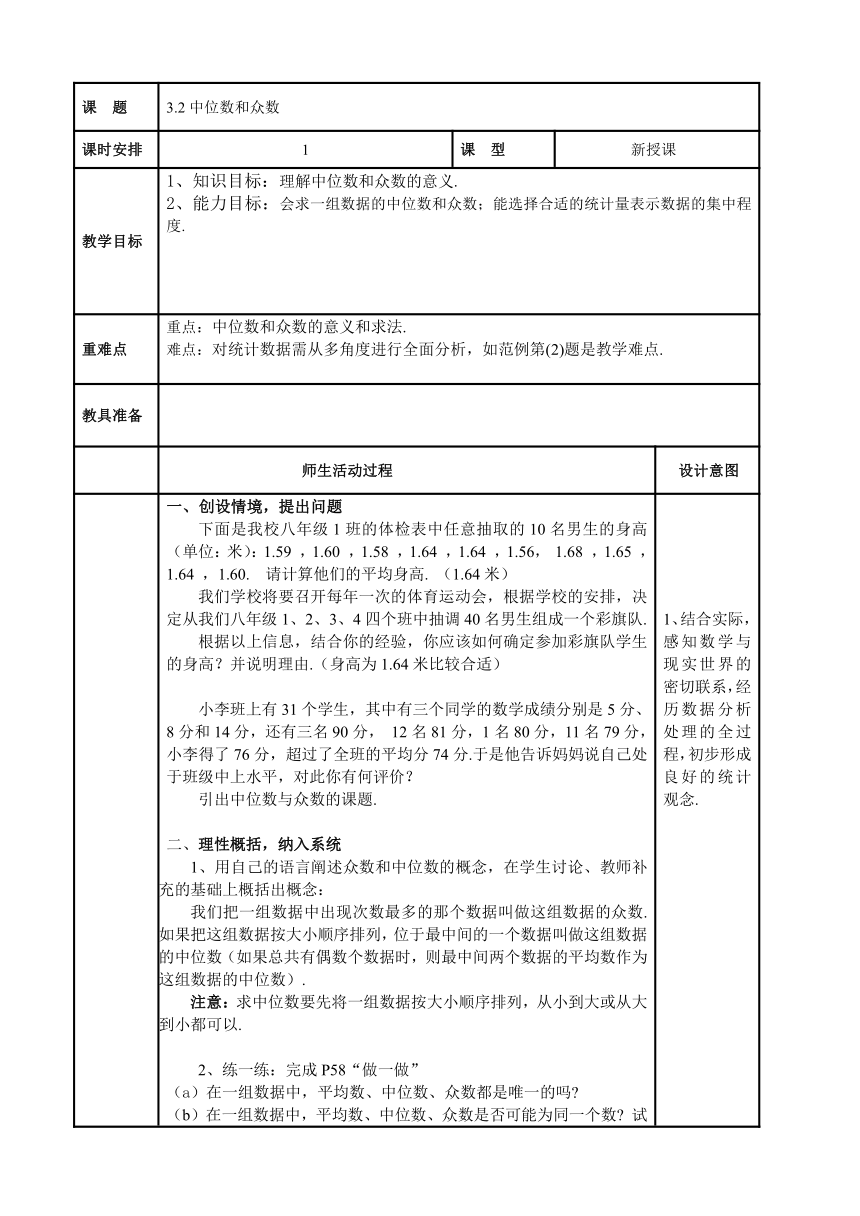
上课日期: 年 月 日 第 课时
课 题 3.1平均数
课时安排 1 课 型 新授课
教学目标 1、知识目标:理解并会计算平均数、加权平均数.2、能力目标:会根据具体问题选择适当的方法求平均数,会用样本的平均数来估计总体的平均数.
重难点 重点:平均数的计算(包括加权平均数).难点:例2的问题情境比较复杂,还涉及加权平均数的计算是本节教学难点.
教具准备
师生活动过程 设计意图
一、创设情境,提出问题.1、王大爷为了估计某水库中鱼的条数,第一次捕捞出120条鱼,做上标记后放回水库中,过了一段时间后,第二次又捕捞出300条鱼,发现其中带有记号的鱼有10条。你能帮他估计这个水库中共有多少条鱼吗?在这个问题中,你运用了怎样的统计方法?2、水果在收获前,果农常会先估计果园里果树的产量,你认为应该怎样估计呢 二、启发诱导,探索新知.1、合作学习某果农种植的100棵苹果树即将收获.果品公司在付给果农定金前,需要对这些果树的苹果总产量进行估计.(1)果农任意摘下20个苹果,称得这20个苹果的总质量为4千克.这20个苹果的平均质量是多少千克 (2)果农从100棵苹果树中任意选出10棵,数出这10棵苹果树上的苹果数,得到以下数据(单位:个):154,150,155,155,159,150,152,155,153,157.你能估计出平均每棵树的苹果个数吗 (3)根据上述两个问题,你能估计出这100棵苹果树的苹果总产量吗 2、引出平均数的概念,平均数用符号表示,读做“x拔”,计算平均数公式: 指出:在实践中,常用样本的平均数来估计总体的平均数.例如,在上面的例子中,用20个苹果的平均质量0.2千克来估计100棵苹果树上苹果的平均质量,用10棵树的平均苹果个数154个来估计100棵树的平均苹果个数.3、(1)做一做P56.(2) 练一练:为了调查某一路口某路段的汽车流量,交警记录了一个星期同一时段通过该路口的汽车辆数,记录的 情况如下表:星 期一二三四五六日汽车辆数1009890821008080那么这一星期在该时段通过该路段的汽车平均每天为 辆. 三、学以致用,体验成功.1、讲解P55例2方法(一):直接根据平均数的意义来计算,这里的 指的是什么 n等于多少 方法(二):15个数据中有几个6,几个7,几个8,几个9,几个10 n=15与这些相同数的个数之间有什么关系 所求的平均数的算式还可以写成怎样的算式 2、由上例中的方法(二)概括出加权平均数的概念和权的意义3、讲解P55例2分析:第(1)题只需求一般的平均数,学生容易理解.第(2)题涉及加权平均数,不妨以801班为例,表中相应的3个数据为四、课堂检测.课本P56,课内练习第1,2两题.五、课堂小结及作业布置.通过这节课的学习,你有什么收获 1.知识小结,这节课我们学均数、加权平均数的概念,会计算平均数和加权平均数.2.会用样本的平均数来估计总体的平均数. 1、通过小学里已学过的平均数的概念,学生解决本节引例的实际问题应该没有什么困难,教学中突出利用样本的平均数来估计总体平均数的意义.2、在具体的问题情景中去感受计算平均数,关注社会问题,培养一种社会责任感.
教学反思
上课日期: 年 月 日 第 课时
课 题 3.2中位数和众数
课时安排 1 课 型 新授课
教学目标 1、知识目标:理解中位数和众数的意义.2、能力目标:会求一组数据的中位数和众数;能选择合适的统计量表示数据的集中程度.
重难点 重点:中位数和众数的意义和求法.难点:对统计数据需从多角度进行全面分析,如范例第(2)题是教学难点.
教具准备
师生活动过程 设计意图
创设情境,提出问题下面是我校八年级1班的体检表中任意抽取的10名男生的身高(单位:米):1.59 ,1.60 ,1.58 ,1.64 ,1.64 ,1.56, 1.68 ,1.65 ,1.64 ,1.60. 请计算他们的平均身高. (1.64米)我们学校将要召开每年一次的体育运动会,根据学校的安排,决定从我们八年级1、2、3、4四个班中抽调40名男生组成一个彩旗队. 根据以上信息,结合你的经验,你应该如何确定参加彩旗队学生的身高?并说明理由.(身高为1.64米比较合适)小李班上有31个学生,其中有三个同学的数学成绩分别是5分、8分和14分,还有三名90分, 12名81分,1名80分,11名79分,小李得了76分,超过了全班的平均分74分.于是他告诉妈妈说自己处于班级中上水平,对此你有何评价?引出中位数与众数的课题 ( http: / / www.xkb1.com ).二、理性概括,纳入系统1、用自己的语言阐述众数和中位数的概念,在学生讨论、教师补充的基础上概括出概念:我们把一组数据中出现次数最多的那个数据叫做这组数据的众数.如果把这组数据按大小顺序排列,位于最中间的一个数据叫做这组数据的中位数(如果总共有偶数个数据时,则最中间两个数据的平均数作为这组数据的中位数).注意:求中位数要先将一组数据按大小顺序排列,从小到大或从大到小都可以. 2、练一练:完成P58“做一做”(a)在一组数据中,平均数、中位数、众数都是唯一的吗 (b)在一组数据中,平均数、中位数、众数是否可能为同一个数 试举例说明.①在一组数据申,中位数是唯一的,可能师这组数据中的数据,也可能不是这组数据中的数据.②在一组数据中,众数并不唯一,众数是出现次数最多的数据,而不是次数.众数一定是这组数据中的数据. 3、通过学生自学、讨论的形式,使学生自己对中位数、众数这两个概念进行归纳、整理,通过比较概念之间的区别和联系,揭示概念的实质,形成新的知识结构.3、例:某工程咨询公司技术部门员工一月份的工资报表如下(单位:元)员工总工程师工程师技术员A技术员B技术员C技术员D技术员E技术员F技术员G见习生H工资500040001800170015001200120012001000400 (1)求该公司技术员工一月份工资的平均数、中位数和众数.(2)作为一般技术员,若考虑应聘该公司技术部门工作,该如何看待工资情况?(小结:在一组存在极端值的数据中,用中位数或众数作为表示这组数据特征的统计量有时会更贴近实际)想一想:在歌手大奖赛中,去掉一个最高分和一个最低分,将剩下分数的平均数作为这位歌手的最后得分,为什么?分组讨论后,得出平均数、中位数、众数的适用范围.三、学以致用,体验成功. 1、10位学生在家政课上进行包水饺比赛,在同一时间内包水饺的个数分别为:15,17,14,10,15,19,17,16,14,12.求这10位同学包水饺的个数的中位数. 2、求4 ,6,7,6,5,4这组数据的众数. 3、某面包房在一天内销售面包100个,各类面包销售量如下表:面包种数奶油巧克力豆沙稻香三色椰茸销售量(个)10152551530在这个问题中,如果你是店主,你最关心的是哪一个统计量 四、课堂检测.课本P60课内练习第1,2题.五、课堂小结及作业布置. 1、结合实际,感知数学与现实世界的密切联系,经历数据分析处理的全过程,初步形成良好的统计观念.2、结合具体情境,提出问题,并寻求解决问题的方法,进而获得解决实际问题的经验.
教学反思
上课日期: 年 月 日 第 课时
课 题 3.3方差与标准差
课时安排 1 课 型 新授课
教学目标 1、知识目标:了解方差、标准差的概念. 2、能力目标:会求一组数据的方差、标准差,并会用他们表示数据的离散程度.能用样本的方差来估计总体的方差.
重难点 重点:方差的概念和计算.难点:方差如何表示数据的离散程度,学生不容易理解,是本节教学的难点.
教具准备
师生活动过程 设计意图
一、创设情景,提出问题. 甲、乙两名射击手的测试成绩统计如下表:第一次第二次第三次第四次第五次甲命中环数78889乙命中环数1061068①请分别算出甲、乙两名射击手的平均成绩.②请根据这两名射击手的成绩在图中画出折线图.③ 现要挑选一名射击手参加比赛,若你是教练,你认为挑选哪一位比较适宜?为什么?二、合作交流,感知问题.请根据统计图,思考问题:①甲、乙两名射击手他们每次射击成绩与他们的平均成绩比较,哪一个偏离程度较低?(甲射击成绩与平均成绩的偏差的和:(7-8)+(8-8)+(8-8)+(8-8)+(9-8) =0;乙射击成绩与平均成绩的偏差的和:(10-8)+(6-8)+(10-8)+(6-8)+(8-8) =0)②射击成绩偏离平均数的程度与数据的离散程度与折线的波动情况有怎样的联系?(甲射击成绩与平均成绩的偏差的平方和:(7-8)2+(8-8) 2+(8-8) 2+(8-8) 2+(9-8) 2= 2;乙射击成绩与平均成绩的偏差的平方和:(10-8) 2+(6-8) 2+(10-8) 2+(6-8) 2+(8-8) 2 =16)上述各偏差的平方和的大小还与什么有关?——与射击次数有关! ③用怎样的特征数来表示数据的偏离程度?可否用各个数据与平均的差的累计数来表示数据的偏离程度?④是否可用各个数据与平均数的差的平方和来表示数据的偏离程度?⑤数据的偏离程度还与什么有关?三、概括总结,巩固新知.1、根据以上问题情景,在学生讨论,教师补充的基础上得出方差的概念、计算方法、用方差来判断数据的稳定性.用各偏差平方的平均数来衡量数据的稳定性设一组数据x1、x2、…、xn中,各数据与它们的平均数的差的平方分别是(x1-x)2、(x2-x) 2、… (xn-x) 2,那么我们称它们的平均数,即为这组数据的方差.方差用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)方差的单位和数据的单位不统一,引出标准差的概念.2、例: 为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):甲: 12 13 14 15 10 16 13 11 15 11乙: 11 16 17 14 13 19 6 8 10 16问哪种小麦长得比较整齐 四、课堂检测 课本P64课内练习第1,2题.五、课堂小结及布置作业.1、方差、标准差的概念,方差的实质是各数据与平均数的差的平方的平均数.方差越大,说明数据的波动越大,越不稳定.2、数据a1,a2,a3,…,an的平均数为X,方差为Y,标准差为Z.则①数据a1+b,a2 + b,a3 +b ,…,an +b的平均数为X+b,方差为Y,标准差为Z. ② 数据ma1,ma2 ,ma3 ,…,man的平均数为mX,方差为m2X,标准差为mZ. ③数据ma1+b,ma2 +b,ma3 +b,…,man +b的平均数为mX+b,方差为m2Y,标准差为mZ. 1、通过合作学习中的射击问题,使学生体会到在解决实际问题时,不仅需要用平均数,还需要另外一个表示数据离散程度的特征数.2、通过实际情景,提出问题,并寻求解决问题的方法,培养学生应用数学的意识和能力.
教学反思
上课日期: 年 月 日 第 1 课时
课 题 第3章数据分析初步复习
课时安排 1 课 型 复习课
教学目标 会求一组数据的平均数、加权平均数.会求一组数据的中位数和众数.会求一组数据的方差和标准差.掌握各种统计量的简单实际应用.
重难点 能计算简单数据的方差,方差公式较难记忆,理解方差是用来衡量一批数据的波动大小的;能解释统计结果,根据结果作出简单的判断和预测.
教具准备
师生活动过程 设计意图
一、知识回顾 以前学习的统计量有平均数、中位数、众数、方差、标准差. 平均数、中位数、众数是描述一组数据集中的统计量;方差、标准差是描述一组数据离散程度的统计量. 在实际生活中,我们不仅关注数据的集中程度,也关注数据的离散程度,但反映集中程度的三个统计量也有局限性,如平均数容易受极端值的影响,中位数不能充分利用全部数据信息. 当一组数据出现多个众数时,这时众数就没有多大的意义. 二、例题讲解,知识应用 1、 下列各个判断或做法正确吗?请说明理由. (1) 篮球场上10人的平均年龄是18岁,有人说这一定是一群高中生(或大学生)在打球. (2) 某柜台有A、B、C、D、E五种品牌的同一商品,按销售价格排列顺序为A、B、C、D、E,经过市场调查发现,对该商品消费的平均水平与C品牌的价格相同,所以柜台老板到批发部大量购进C品牌. 解:(1)错,比如2名30岁的老师带着8名15岁的初中生在一起打球. (2) 错,好比消费者在分别大量购买了价格比C品牌高和比C品牌低的其他商品后,其平均消费水平也有可能和C品牌的价格相当. 注:(1)中最好利用平均数、中位数和众数一起判断更为精确. (2)中进货的依据应该是众数,而不是平均数. 2、8名学生在一次数学测试中的成绩为80,82,79,69,74,78,x,81,这组成绩的平均数是77,则x的值为_______.3、某小组6名同学在期中考试中数学成绩(单位:分)分别是120、130、140、150、125、130这组数据的中位数是________.4、四个数据8,10,x,10的平均数与中位数相等,则x等于________. 5、有一组数据:3,4,5,6,6,则下列四个结论中正确的是( ) A. 这组数据的平均数、众数、中位数分别是4.8,6,6B. 这组数据的平均数、众数、中位数分别是5,5,5C. 这组数据的平均数、众数、中位数分别是4.8,6,5D. 这组数据的平均数、众数、中位数分别是5,6,66、如果一组数据的方差为4,那么将每个数据都减去3,则所得的一组新数据的标准差是________. 7、将一组数据中的每一个数减去50后,所得新的一组数据的平均数是2,则原来那组数据的平均数是________.8、一组数据2,7,6,3,4, 7的众数和中位数分别是________. 9、有22位同学参加智力竞赛,他们的分数互不相同,按分数高低选11位同学进入下一轮比赛,小明知道了自己的分数后,还需知道哪个统计量________,就能判断自己能否进入下一轮比赛.10、某校九年级(1)班有7个合作学习小组,各学习小组的人数分别为:5,6,6,x,7,8,9,已知这组数据的平均数是7,则这组数据的中位数是________. 10、甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均成绩都相同,方差分别是,则射箭成绩最稳定的是________. 三、知识巩固. 练习:书本P70页本章小结. 四、课堂小结及布置作业.若要知道数据的集中程度,则应求数据的平均数、中位数和众数.若要知道数据的离散程度,则应求数据的方差或标准差.
教学反思
课 题 3.1平均数
课时安排 1 课 型 新授课
教学目标 1、知识目标:理解并会计算平均数、加权平均数.2、能力目标:会根据具体问题选择适当的方法求平均数,会用样本的平均数来估计总体的平均数.
重难点 重点:平均数的计算(包括加权平均数).难点:例2的问题情境比较复杂,还涉及加权平均数的计算是本节教学难点.
教具准备
师生活动过程 设计意图
一、创设情境,提出问题.1、王大爷为了估计某水库中鱼的条数,第一次捕捞出120条鱼,做上标记后放回水库中,过了一段时间后,第二次又捕捞出300条鱼,发现其中带有记号的鱼有10条。你能帮他估计这个水库中共有多少条鱼吗?在这个问题中,你运用了怎样的统计方法?2、水果在收获前,果农常会先估计果园里果树的产量,你认为应该怎样估计呢 二、启发诱导,探索新知.1、合作学习某果农种植的100棵苹果树即将收获.果品公司在付给果农定金前,需要对这些果树的苹果总产量进行估计.(1)果农任意摘下20个苹果,称得这20个苹果的总质量为4千克.这20个苹果的平均质量是多少千克 (2)果农从100棵苹果树中任意选出10棵,数出这10棵苹果树上的苹果数,得到以下数据(单位:个):154,150,155,155,159,150,152,155,153,157.你能估计出平均每棵树的苹果个数吗 (3)根据上述两个问题,你能估计出这100棵苹果树的苹果总产量吗 2、引出平均数的概念,平均数用符号表示,读做“x拔”,计算平均数公式: 指出:在实践中,常用样本的平均数来估计总体的平均数.例如,在上面的例子中,用20个苹果的平均质量0.2千克来估计100棵苹果树上苹果的平均质量,用10棵树的平均苹果个数154个来估计100棵树的平均苹果个数.3、(1)做一做P56.(2) 练一练:为了调查某一路口某路段的汽车流量,交警记录了一个星期同一时段通过该路口的汽车辆数,记录的 情况如下表:星 期一二三四五六日汽车辆数1009890821008080那么这一星期在该时段通过该路段的汽车平均每天为 辆. 三、学以致用,体验成功.1、讲解P55例2方法(一):直接根据平均数的意义来计算,这里的 指的是什么 n等于多少 方法(二):15个数据中有几个6,几个7,几个8,几个9,几个10 n=15与这些相同数的个数之间有什么关系 所求的平均数的算式还可以写成怎样的算式 2、由上例中的方法(二)概括出加权平均数的概念和权的意义3、讲解P55例2分析:第(1)题只需求一般的平均数,学生容易理解.第(2)题涉及加权平均数,不妨以801班为例,表中相应的3个数据为四、课堂检测.课本P56,课内练习第1,2两题.五、课堂小结及作业布置.通过这节课的学习,你有什么收获 1.知识小结,这节课我们学均数、加权平均数的概念,会计算平均数和加权平均数.2.会用样本的平均数来估计总体的平均数. 1、通过小学里已学过的平均数的概念,学生解决本节引例的实际问题应该没有什么困难,教学中突出利用样本的平均数来估计总体平均数的意义.2、在具体的问题情景中去感受计算平均数,关注社会问题,培养一种社会责任感.
教学反思
上课日期: 年 月 日 第 课时
课 题 3.2中位数和众数
课时安排 1 课 型 新授课
教学目标 1、知识目标:理解中位数和众数的意义.2、能力目标:会求一组数据的中位数和众数;能选择合适的统计量表示数据的集中程度.
重难点 重点:中位数和众数的意义和求法.难点:对统计数据需从多角度进行全面分析,如范例第(2)题是教学难点.
教具准备
师生活动过程 设计意图
创设情境,提出问题下面是我校八年级1班的体检表中任意抽取的10名男生的身高(单位:米):1.59 ,1.60 ,1.58 ,1.64 ,1.64 ,1.56, 1.68 ,1.65 ,1.64 ,1.60. 请计算他们的平均身高. (1.64米)我们学校将要召开每年一次的体育运动会,根据学校的安排,决定从我们八年级1、2、3、4四个班中抽调40名男生组成一个彩旗队. 根据以上信息,结合你的经验,你应该如何确定参加彩旗队学生的身高?并说明理由.(身高为1.64米比较合适)小李班上有31个学生,其中有三个同学的数学成绩分别是5分、8分和14分,还有三名90分, 12名81分,1名80分,11名79分,小李得了76分,超过了全班的平均分74分.于是他告诉妈妈说自己处于班级中上水平,对此你有何评价?引出中位数与众数的课题 ( http: / / www.xkb1.com ).二、理性概括,纳入系统1、用自己的语言阐述众数和中位数的概念,在学生讨论、教师补充的基础上概括出概念:我们把一组数据中出现次数最多的那个数据叫做这组数据的众数.如果把这组数据按大小顺序排列,位于最中间的一个数据叫做这组数据的中位数(如果总共有偶数个数据时,则最中间两个数据的平均数作为这组数据的中位数).注意:求中位数要先将一组数据按大小顺序排列,从小到大或从大到小都可以. 2、练一练:完成P58“做一做”(a)在一组数据中,平均数、中位数、众数都是唯一的吗 (b)在一组数据中,平均数、中位数、众数是否可能为同一个数 试举例说明.①在一组数据申,中位数是唯一的,可能师这组数据中的数据,也可能不是这组数据中的数据.②在一组数据中,众数并不唯一,众数是出现次数最多的数据,而不是次数.众数一定是这组数据中的数据. 3、通过学生自学、讨论的形式,使学生自己对中位数、众数这两个概念进行归纳、整理,通过比较概念之间的区别和联系,揭示概念的实质,形成新的知识结构.3、例:某工程咨询公司技术部门员工一月份的工资报表如下(单位:元)员工总工程师工程师技术员A技术员B技术员C技术员D技术员E技术员F技术员G见习生H工资500040001800170015001200120012001000400 (1)求该公司技术员工一月份工资的平均数、中位数和众数.(2)作为一般技术员,若考虑应聘该公司技术部门工作,该如何看待工资情况?(小结:在一组存在极端值的数据中,用中位数或众数作为表示这组数据特征的统计量有时会更贴近实际)想一想:在歌手大奖赛中,去掉一个最高分和一个最低分,将剩下分数的平均数作为这位歌手的最后得分,为什么?分组讨论后,得出平均数、中位数、众数的适用范围.三、学以致用,体验成功. 1、10位学生在家政课上进行包水饺比赛,在同一时间内包水饺的个数分别为:15,17,14,10,15,19,17,16,14,12.求这10位同学包水饺的个数的中位数. 2、求4 ,6,7,6,5,4这组数据的众数. 3、某面包房在一天内销售面包100个,各类面包销售量如下表:面包种数奶油巧克力豆沙稻香三色椰茸销售量(个)10152551530在这个问题中,如果你是店主,你最关心的是哪一个统计量 四、课堂检测.课本P60课内练习第1,2题.五、课堂小结及作业布置. 1、结合实际,感知数学与现实世界的密切联系,经历数据分析处理的全过程,初步形成良好的统计观念.2、结合具体情境,提出问题,并寻求解决问题的方法,进而获得解决实际问题的经验.
教学反思
上课日期: 年 月 日 第 课时
课 题 3.3方差与标准差
课时安排 1 课 型 新授课
教学目标 1、知识目标:了解方差、标准差的概念. 2、能力目标:会求一组数据的方差、标准差,并会用他们表示数据的离散程度.能用样本的方差来估计总体的方差.
重难点 重点:方差的概念和计算.难点:方差如何表示数据的离散程度,学生不容易理解,是本节教学的难点.
教具准备
师生活动过程 设计意图
一、创设情景,提出问题. 甲、乙两名射击手的测试成绩统计如下表:第一次第二次第三次第四次第五次甲命中环数78889乙命中环数1061068①请分别算出甲、乙两名射击手的平均成绩.②请根据这两名射击手的成绩在图中画出折线图.③ 现要挑选一名射击手参加比赛,若你是教练,你认为挑选哪一位比较适宜?为什么?二、合作交流,感知问题.请根据统计图,思考问题:①甲、乙两名射击手他们每次射击成绩与他们的平均成绩比较,哪一个偏离程度较低?(甲射击成绩与平均成绩的偏差的和:(7-8)+(8-8)+(8-8)+(8-8)+(9-8) =0;乙射击成绩与平均成绩的偏差的和:(10-8)+(6-8)+(10-8)+(6-8)+(8-8) =0)②射击成绩偏离平均数的程度与数据的离散程度与折线的波动情况有怎样的联系?(甲射击成绩与平均成绩的偏差的平方和:(7-8)2+(8-8) 2+(8-8) 2+(8-8) 2+(9-8) 2= 2;乙射击成绩与平均成绩的偏差的平方和:(10-8) 2+(6-8) 2+(10-8) 2+(6-8) 2+(8-8) 2 =16)上述各偏差的平方和的大小还与什么有关?——与射击次数有关! ③用怎样的特征数来表示数据的偏离程度?可否用各个数据与平均的差的累计数来表示数据的偏离程度?④是否可用各个数据与平均数的差的平方和来表示数据的偏离程度?⑤数据的偏离程度还与什么有关?三、概括总结,巩固新知.1、根据以上问题情景,在学生讨论,教师补充的基础上得出方差的概念、计算方法、用方差来判断数据的稳定性.用各偏差平方的平均数来衡量数据的稳定性设一组数据x1、x2、…、xn中,各数据与它们的平均数的差的平方分别是(x1-x)2、(x2-x) 2、… (xn-x) 2,那么我们称它们的平均数,即为这组数据的方差.方差用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)方差的单位和数据的单位不统一,引出标准差的概念.2、例: 为了考察甲、乙两种小麦的长势,分别从中抽出10株苗,测得苗高如下(单位:cm):甲: 12 13 14 15 10 16 13 11 15 11乙: 11 16 17 14 13 19 6 8 10 16问哪种小麦长得比较整齐 四、课堂检测 课本P64课内练习第1,2题.五、课堂小结及布置作业.1、方差、标准差的概念,方差的实质是各数据与平均数的差的平方的平均数.方差越大,说明数据的波动越大,越不稳定.2、数据a1,a2,a3,…,an的平均数为X,方差为Y,标准差为Z.则①数据a1+b,a2 + b,a3 +b ,…,an +b的平均数为X+b,方差为Y,标准差为Z. ② 数据ma1,ma2 ,ma3 ,…,man的平均数为mX,方差为m2X,标准差为mZ. ③数据ma1+b,ma2 +b,ma3 +b,…,man +b的平均数为mX+b,方差为m2Y,标准差为mZ. 1、通过合作学习中的射击问题,使学生体会到在解决实际问题时,不仅需要用平均数,还需要另外一个表示数据离散程度的特征数.2、通过实际情景,提出问题,并寻求解决问题的方法,培养学生应用数学的意识和能力.
教学反思
上课日期: 年 月 日 第 1 课时
课 题 第3章数据分析初步复习
课时安排 1 课 型 复习课
教学目标 会求一组数据的平均数、加权平均数.会求一组数据的中位数和众数.会求一组数据的方差和标准差.掌握各种统计量的简单实际应用.
重难点 能计算简单数据的方差,方差公式较难记忆,理解方差是用来衡量一批数据的波动大小的;能解释统计结果,根据结果作出简单的判断和预测.
教具准备
师生活动过程 设计意图
一、知识回顾 以前学习的统计量有平均数、中位数、众数、方差、标准差. 平均数、中位数、众数是描述一组数据集中的统计量;方差、标准差是描述一组数据离散程度的统计量. 在实际生活中,我们不仅关注数据的集中程度,也关注数据的离散程度,但反映集中程度的三个统计量也有局限性,如平均数容易受极端值的影响,中位数不能充分利用全部数据信息. 当一组数据出现多个众数时,这时众数就没有多大的意义. 二、例题讲解,知识应用 1、 下列各个判断或做法正确吗?请说明理由. (1) 篮球场上10人的平均年龄是18岁,有人说这一定是一群高中生(或大学生)在打球. (2) 某柜台有A、B、C、D、E五种品牌的同一商品,按销售价格排列顺序为A、B、C、D、E,经过市场调查发现,对该商品消费的平均水平与C品牌的价格相同,所以柜台老板到批发部大量购进C品牌. 解:(1)错,比如2名30岁的老师带着8名15岁的初中生在一起打球. (2) 错,好比消费者在分别大量购买了价格比C品牌高和比C品牌低的其他商品后,其平均消费水平也有可能和C品牌的价格相当. 注:(1)中最好利用平均数、中位数和众数一起判断更为精确. (2)中进货的依据应该是众数,而不是平均数. 2、8名学生在一次数学测试中的成绩为80,82,79,69,74,78,x,81,这组成绩的平均数是77,则x的值为_______.3、某小组6名同学在期中考试中数学成绩(单位:分)分别是120、130、140、150、125、130这组数据的中位数是________.4、四个数据8,10,x,10的平均数与中位数相等,则x等于________. 5、有一组数据:3,4,5,6,6,则下列四个结论中正确的是( ) A. 这组数据的平均数、众数、中位数分别是4.8,6,6B. 这组数据的平均数、众数、中位数分别是5,5,5C. 这组数据的平均数、众数、中位数分别是4.8,6,5D. 这组数据的平均数、众数、中位数分别是5,6,66、如果一组数据的方差为4,那么将每个数据都减去3,则所得的一组新数据的标准差是________. 7、将一组数据中的每一个数减去50后,所得新的一组数据的平均数是2,则原来那组数据的平均数是________.8、一组数据2,7,6,3,4, 7的众数和中位数分别是________. 9、有22位同学参加智力竞赛,他们的分数互不相同,按分数高低选11位同学进入下一轮比赛,小明知道了自己的分数后,还需知道哪个统计量________,就能判断自己能否进入下一轮比赛.10、某校九年级(1)班有7个合作学习小组,各学习小组的人数分别为:5,6,6,x,7,8,9,已知这组数据的平均数是7,则这组数据的中位数是________. 10、甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均成绩都相同,方差分别是,则射箭成绩最稳定的是________. 三、知识巩固. 练习:书本P70页本章小结. 四、课堂小结及布置作业.若要知道数据的集中程度,则应求数据的平均数、中位数和众数.若要知道数据的离散程度,则应求数据的方差或标准差.
教学反思
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
