浙教版八年级下册第二章 一元二次方程教案
文档属性
| 名称 | 浙教版八年级下册第二章 一元二次方程教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 73.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-23 19:15:48 | ||
图片预览



文档简介
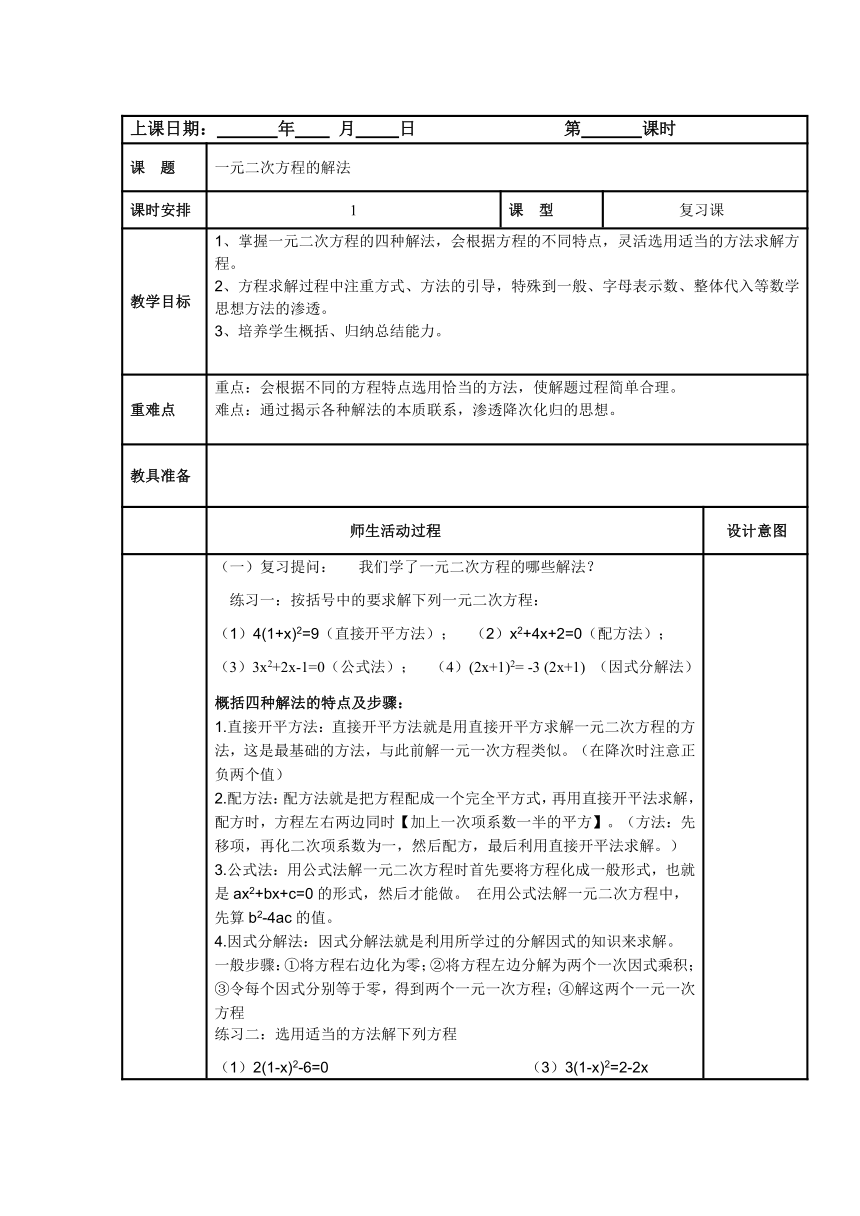
上课日期: 年 月 日 第 课时
课 题 一元二次方程的解法
课时安排 1 课 型 复习课
教学目标 1、掌握一元二次方程的四种解法,会根据方程的不同特点,灵活选用适当的方法求解方程。2、方程求解过程中注重方式、方法的引导,特殊到一般、字母表示数、整体代入等数学思想方法的渗透。3、培养学生概括、归纳总结能力。
重难点 重点:会根据不同的方程特点选用恰当的方法,使解题过程简单合理。难点:通过揭示各种解法的本质联系,渗透降次化归的思想。
教具准备
师生活动过程 设计意图
(一)复习提问: 我们学了一元二次方程的哪些解法?练习一:按括号中的要求解下列一元二次方程:(1)4(1+x)2=9(直接开平方法); (2)x2+4x+2=0(配方法);(3)3x2+2x-1=0(公式法); (4)(2x+1)2= -3 (2x+1) (因式分解法)概括四种解法的特点及步骤:1.直接开平方法:直接开平方法就是用直接开平方求解一元二次方程的方法,这是最基础的方法,与此前解一元一次方程类似。(在降次时注意正负两个值)2.配方法:配方法就是把方程配成一个完全平方式,再用直接开平法求解,配方时,方程左右两边同时【加上一次项系数一半的平方】。(方法:先移项,再化二次项系数为一,然后配方,最后利用直接开平法求解。)3.公式法:用公式法解一元二次方程时首先要将方程化成一般形式,也就是ax2+bx+c=0的形式,然后才能做。 在用公式法解一元二次方程中,先算b2-4ac的值。 4.因式分解法:因式分解法就是利用所学过的分解因式的知识来求解。一般步骤:①将方程右边化为零;②将方程左边分解为两个一次因式乘积;③令每个因式分别等于零,得到两个一元一次方程;④解这两个一元一次方程练习二:选用适当的方法解下列方程 (1)2(1-x)2-6=0 (3)3(1-x)2=2-2x (2)(2x-1)+3(2x-1)+2=0; (4)(x+2)(x+3)=6交流讨论:1 与同桌或邻桌同学比较,看谁的解法更简单。2 你如何根据方程的特征选择解法?概括:1、当给定的一元二次方程通过适当变形可化为型时,可选用直接开平方法。2、当一元二次方程的左边能分解因式时,用因式分解法比较简单。3、当一元二次方程中a,b,c不缺项且不易分解因式时,一般采用公式法。4、配方法也是一种重要的解题方法,但步骤较为繁琐,所以只要没要求时,一般不采用此法。但对于一次项系数较小而常数项较大时 ,可选用此法5、四种方法中,优先选取顺序为:直接开平方法、因式分解法、公式法、配方法(二)、延伸拓展:1、配方法应用举例:已知代数式x2 – 6x+10 ,(1)试说明无论x取何实数时,代数式的值都大于0.(2)求代数式的最小值.(三)课堂小结:(1)说说你对解一元二次方程的感受:(2)四种方法(直接开平方法、配方法、公式法、因式分解法)的联系与区别:
教学反思
上课日期: 年 月 日 第 课时
课 题 2.1-2.2复习
课时安排 1 课 型 复习课
教学目标 1.掌握一元二次方程的定义,会把一个一元二次方程写成一般形式。2.掌握一元二次方程的四种解法3.掌握一元二次方程根的判别式,并会用根的判别式判断一元二次方程根的情况。
重难点 重点:会根据不同的方程特点选用恰当的方法解一元二次方程,使解题过程简单合理。难点:通过揭示各种解法的本质联系,渗透降次化归的思想。
教具准备
师生活动过程 设计意图
例1 已知关于x的方程x2-5x+m-1=0的一个根与关于x的方程x2+5x-m+1=0的一个根互为相反数,求m的值.例2 解方程:(1)9(x-1)2=4;(2)x2-10x+9=0;(3)x2-3x-1=0;(4)(x-3)2+1=2(x-3).例3 已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a,b,c分别为△ABC三边.(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.课后练习1. 下面关于x的方程中:①ax2+bx+c=0;②3(x-9)2-(x+1)2=1;③x+3=;④(a2+1)x2-a=0;⑤=x-1. 一元二次方程的个数是( ) A.1 B.2 C.3 D.42. 若一元二次方程ax2+bx+c=0有一个根为-1,则( ) A.a+b+c=0 B.a-b+c=0 C.a+b+c=1 D.a-b+c=13. (兰州中考)如果一元二次方程2x2+3x+m=0有两个相等的实数根,那么实数m的取值为( ) A. m> B. m> C. m= D. m=4. 若(x+y)(1-x-y)+6=0,则x+y的值是( ) A.2 B.3 C.-2或3 D.2或-35. 把一元二次方程(x-3)2=4化为一般形式为: ,二次项为 ,一次项系数为 ,常数项为 .6. 已知方程x2+kx+3=0的一个根是-1,则k= ,另一根为 .7. 若方程(x-1)(x+2)=0的两根为x1,x2,且x1>x2,则x1-2x2= .8. 若一个三角形的边长均满足方程x2-6x+8=0,则此三角形的周长为 .9. 已知m,n都是方程x2+2016x+2017=0的根,则代数式(m2+2016m-2017)(n2+2016n+2016)的值为 .10. 解下列一元二次方程:(1)x2+3x+1=0;(2)x2-3x+2=0;(3)(x+1)(x-1)=2x;(4)(x-1)(x+2)=2(x+2).11. 求证:关于x的方程x2+(2k+1)x+k-1=0有两个不相等的实数根.12. 若n(n≠0)是关于x的方程x2+mx-9n=0的根,求的值.
教学反思
上课日期: 年 月 日 第 课时
课 题 2.3-2.4复习
课时安排 1 课 型 复习
教学目标 掌握用一元二次方程解决实际问题的基本步骤。平均增长率问题,面积问题,销售问题重点要掌握。进一步增强学生的理解能力。
重难点 重点:平均增长率问题,面积问题,销售问题难点:理解实际问题,选择解决问题的数学模型
教具准备
师生活动过程 设计意图
例1 某地地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动. 第一天收到捐款10000元,第三天收到捐款12100元.(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?例2 某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售,销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,问第二周每个旅游纪念品的销售价格为多少元?课后练习1. (无锡中考)某商店今年1月份的销售额是2万元,3月份的销售额是4.5万元,从1月份到3月份,该店销售额平均每月的增长率是( )A.20% B.25% C.50% D.62.5%3. 一个面积为120m2的长方形苗圃,它的长比宽多2m,则该苗圃的长是( ) A.10m B.12m C.13m D.14m4. 要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排21场比赛,则参赛球队的个数是( ) A.5个 B.6个 C.7个 D.8个6. 某服装厂生产一批西服,原来每件的成本价是500元,销售价为625元,经市场预测,该产品销售价第一个月将降低20%,第二个月比第一个月提高6%,为了使两个月后的销售利润达到原来水平,该产品的成本价平均每月应降低百分之几?7. 一个三位数,十位数字比百位数字大3,个位数字等于百位数字与十位数字的和,且这个三位数比个位数字的平方的5倍大12,求这个三位数.8. 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2100元,每件衬衫应降价多少元?9. 有一批图形计算器,原售价为每台800元,在甲、乙两家公司销售. 甲公司用如下方法促销:买一台单价为780元;买两台,每台都为760元. 依次类推,即每多买一台,所买各台单价均再减20元,但最低不能低于每台440元. 乙公司一律按原售价的75%促销. 某单位需购买一批图形计算器:(1)若此单位需购买6台图形计算器,应去哪家公司购买花费较少?(2)若此单位恰好花费7500元在同一家公司购买了一定数量的图形计算器,请问是在哪家公司购买的?数量是多少?
教学反思
课 题 一元二次方程的解法
课时安排 1 课 型 复习课
教学目标 1、掌握一元二次方程的四种解法,会根据方程的不同特点,灵活选用适当的方法求解方程。2、方程求解过程中注重方式、方法的引导,特殊到一般、字母表示数、整体代入等数学思想方法的渗透。3、培养学生概括、归纳总结能力。
重难点 重点:会根据不同的方程特点选用恰当的方法,使解题过程简单合理。难点:通过揭示各种解法的本质联系,渗透降次化归的思想。
教具准备
师生活动过程 设计意图
(一)复习提问: 我们学了一元二次方程的哪些解法?练习一:按括号中的要求解下列一元二次方程:(1)4(1+x)2=9(直接开平方法); (2)x2+4x+2=0(配方法);(3)3x2+2x-1=0(公式法); (4)(2x+1)2= -3 (2x+1) (因式分解法)概括四种解法的特点及步骤:1.直接开平方法:直接开平方法就是用直接开平方求解一元二次方程的方法,这是最基础的方法,与此前解一元一次方程类似。(在降次时注意正负两个值)2.配方法:配方法就是把方程配成一个完全平方式,再用直接开平法求解,配方时,方程左右两边同时【加上一次项系数一半的平方】。(方法:先移项,再化二次项系数为一,然后配方,最后利用直接开平法求解。)3.公式法:用公式法解一元二次方程时首先要将方程化成一般形式,也就是ax2+bx+c=0的形式,然后才能做。 在用公式法解一元二次方程中,先算b2-4ac的值。 4.因式分解法:因式分解法就是利用所学过的分解因式的知识来求解。一般步骤:①将方程右边化为零;②将方程左边分解为两个一次因式乘积;③令每个因式分别等于零,得到两个一元一次方程;④解这两个一元一次方程练习二:选用适当的方法解下列方程 (1)2(1-x)2-6=0 (3)3(1-x)2=2-2x (2)(2x-1)+3(2x-1)+2=0; (4)(x+2)(x+3)=6交流讨论:1 与同桌或邻桌同学比较,看谁的解法更简单。2 你如何根据方程的特征选择解法?概括:1、当给定的一元二次方程通过适当变形可化为型时,可选用直接开平方法。2、当一元二次方程的左边能分解因式时,用因式分解法比较简单。3、当一元二次方程中a,b,c不缺项且不易分解因式时,一般采用公式法。4、配方法也是一种重要的解题方法,但步骤较为繁琐,所以只要没要求时,一般不采用此法。但对于一次项系数较小而常数项较大时 ,可选用此法5、四种方法中,优先选取顺序为:直接开平方法、因式分解法、公式法、配方法(二)、延伸拓展:1、配方法应用举例:已知代数式x2 – 6x+10 ,(1)试说明无论x取何实数时,代数式的值都大于0.(2)求代数式的最小值.(三)课堂小结:(1)说说你对解一元二次方程的感受:(2)四种方法(直接开平方法、配方法、公式法、因式分解法)的联系与区别:
教学反思
上课日期: 年 月 日 第 课时
课 题 2.1-2.2复习
课时安排 1 课 型 复习课
教学目标 1.掌握一元二次方程的定义,会把一个一元二次方程写成一般形式。2.掌握一元二次方程的四种解法3.掌握一元二次方程根的判别式,并会用根的判别式判断一元二次方程根的情况。
重难点 重点:会根据不同的方程特点选用恰当的方法解一元二次方程,使解题过程简单合理。难点:通过揭示各种解法的本质联系,渗透降次化归的思想。
教具准备
师生活动过程 设计意图
例1 已知关于x的方程x2-5x+m-1=0的一个根与关于x的方程x2+5x-m+1=0的一个根互为相反数,求m的值.例2 解方程:(1)9(x-1)2=4;(2)x2-10x+9=0;(3)x2-3x-1=0;(4)(x-3)2+1=2(x-3).例3 已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a,b,c分别为△ABC三边.(1)如果x=-1是方程的根,试判断△ABC的形状,并说明理由;(2)如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.课后练习1. 下面关于x的方程中:①ax2+bx+c=0;②3(x-9)2-(x+1)2=1;③x+3=;④(a2+1)x2-a=0;⑤=x-1. 一元二次方程的个数是( ) A.1 B.2 C.3 D.42. 若一元二次方程ax2+bx+c=0有一个根为-1,则( ) A.a+b+c=0 B.a-b+c=0 C.a+b+c=1 D.a-b+c=13. (兰州中考)如果一元二次方程2x2+3x+m=0有两个相等的实数根,那么实数m的取值为( ) A. m> B. m> C. m= D. m=4. 若(x+y)(1-x-y)+6=0,则x+y的值是( ) A.2 B.3 C.-2或3 D.2或-35. 把一元二次方程(x-3)2=4化为一般形式为: ,二次项为 ,一次项系数为 ,常数项为 .6. 已知方程x2+kx+3=0的一个根是-1,则k= ,另一根为 .7. 若方程(x-1)(x+2)=0的两根为x1,x2,且x1>x2,则x1-2x2= .8. 若一个三角形的边长均满足方程x2-6x+8=0,则此三角形的周长为 .9. 已知m,n都是方程x2+2016x+2017=0的根,则代数式(m2+2016m-2017)(n2+2016n+2016)的值为 .10. 解下列一元二次方程:(1)x2+3x+1=0;(2)x2-3x+2=0;(3)(x+1)(x-1)=2x;(4)(x-1)(x+2)=2(x+2).11. 求证:关于x的方程x2+(2k+1)x+k-1=0有两个不相等的实数根.12. 若n(n≠0)是关于x的方程x2+mx-9n=0的根,求的值.
教学反思
上课日期: 年 月 日 第 课时
课 题 2.3-2.4复习
课时安排 1 课 型 复习
教学目标 掌握用一元二次方程解决实际问题的基本步骤。平均增长率问题,面积问题,销售问题重点要掌握。进一步增强学生的理解能力。
重难点 重点:平均增长率问题,面积问题,销售问题难点:理解实际问题,选择解决问题的数学模型
教具准备
师生活动过程 设计意图
例1 某地地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动. 第一天收到捐款10000元,第三天收到捐款12100元.(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?例2 某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售,销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,问第二周每个旅游纪念品的销售价格为多少元?课后练习1. (无锡中考)某商店今年1月份的销售额是2万元,3月份的销售额是4.5万元,从1月份到3月份,该店销售额平均每月的增长率是( )A.20% B.25% C.50% D.62.5%3. 一个面积为120m2的长方形苗圃,它的长比宽多2m,则该苗圃的长是( ) A.10m B.12m C.13m D.14m4. 要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排21场比赛,则参赛球队的个数是( ) A.5个 B.6个 C.7个 D.8个6. 某服装厂生产一批西服,原来每件的成本价是500元,销售价为625元,经市场预测,该产品销售价第一个月将降低20%,第二个月比第一个月提高6%,为了使两个月后的销售利润达到原来水平,该产品的成本价平均每月应降低百分之几?7. 一个三位数,十位数字比百位数字大3,个位数字等于百位数字与十位数字的和,且这个三位数比个位数字的平方的5倍大12,求这个三位数.8. 某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2100元,每件衬衫应降价多少元?9. 有一批图形计算器,原售价为每台800元,在甲、乙两家公司销售. 甲公司用如下方法促销:买一台单价为780元;买两台,每台都为760元. 依次类推,即每多买一台,所买各台单价均再减20元,但最低不能低于每台440元. 乙公司一律按原售价的75%促销. 某单位需购买一批图形计算器:(1)若此单位需购买6台图形计算器,应去哪家公司购买花费较少?(2)若此单位恰好花费7500元在同一家公司购买了一定数量的图形计算器,请问是在哪家公司购买的?数量是多少?
教学反思
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
