【核心素养目标】3.2简单几何体的三视图(3) 教学设计
文档属性
| 名称 | 【核心素养目标】3.2简单几何体的三视图(3) 教学设计 |
|
|
| 格式 | doc | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙教版九年级下册数学3.2简单几何体的三视图(3) 教学设计
课题 3.2简单几何体的三视图(3) 单元 第3单元 学科 数学 年级 九
教材分析 本节内容是浙教版九年级下册数学3.2简单几何体的三视图第3课时的内容。从第3节的整体来看,是本章的重点部分,是培养空间想象能力和读图能力的关键一章,起着承上启下的作用,本节课着重培养学生分析和解决问题的能力。本节课是在前面已学过画单独图形的三视图之后的一节比较综合的新授课,对于同学们空间思维能力和空间想象能力也会有较大的提升。
核心素养分析 本节课通过有趣的提问和动手实践激发学生的学习兴趣,利用多媒体动画课件直观生动的讲解,降低学习难度,增强学生学习自信心,变被动学习为主动学习,有利于掌握知识,培养学生自主分析判断问题、解决问题的能力,培养学生达到一定的语言表达能力。
学习目标 1.能够根据不同的物体,学会判断组合体的类型,分析选择主视图,并画出三视图。2.通过画、量、讲等各种学习形式,进一步提高学生的绘图能力,提高空间思维和空间想象能力。3.通过进一步熟悉画三视图,培养协作能力和团队精神,树立科学严谨的学习态度。
重点 通过对组合体形状分析,会画组合体的三视图。
难点 通过“分”“合”的方法,将图形化繁为简,单独画出基本体的三个视图,再将所有基本体组合起来。
教学过程
教学环节 教师活动 学生活动 设计意图
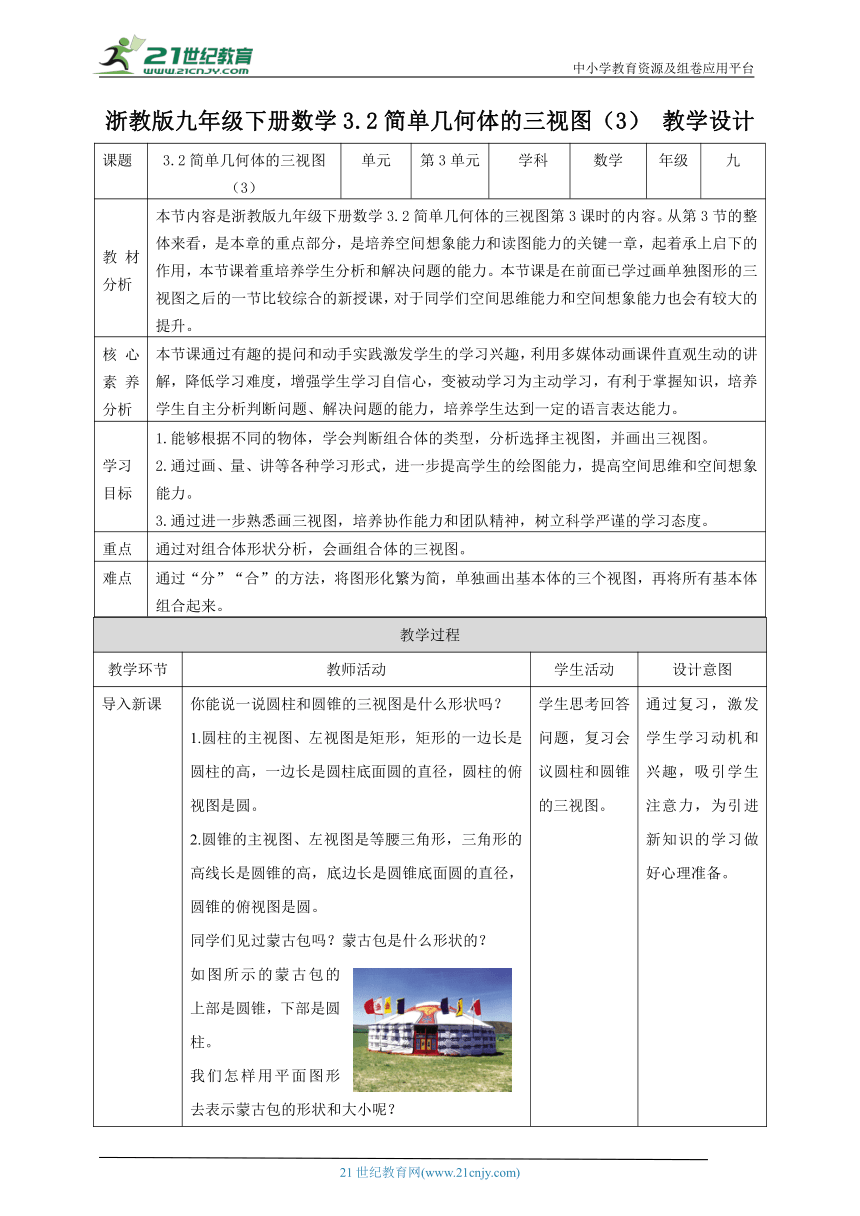
导入新课 你能说一说圆柱和圆锥的三视图是什么形状吗?1.圆柱的主视图、左视图是矩形,矩形的一边长是圆柱的高,一边长是圆柱底面圆的直径,圆柱的俯视图是圆。2.圆锥的主视图、左视图是等腰三角形,三角形的高线长是圆锥的高,底边长是圆锥底面圆的直径,圆锥的俯视图是圆。同学们见过蒙古包吗?蒙古包是什么形状的?如图所示的蒙古包的上部是圆锥,下部是圆柱。我们怎样用平面图形去表示蒙古包的形状和大小呢? 学生思考回答问题,复习会议圆柱和圆锥的三视图。 通过复习,激发学生学习动机和兴趣,吸引学生注意力,为引进新知识的学习做好心理准备。
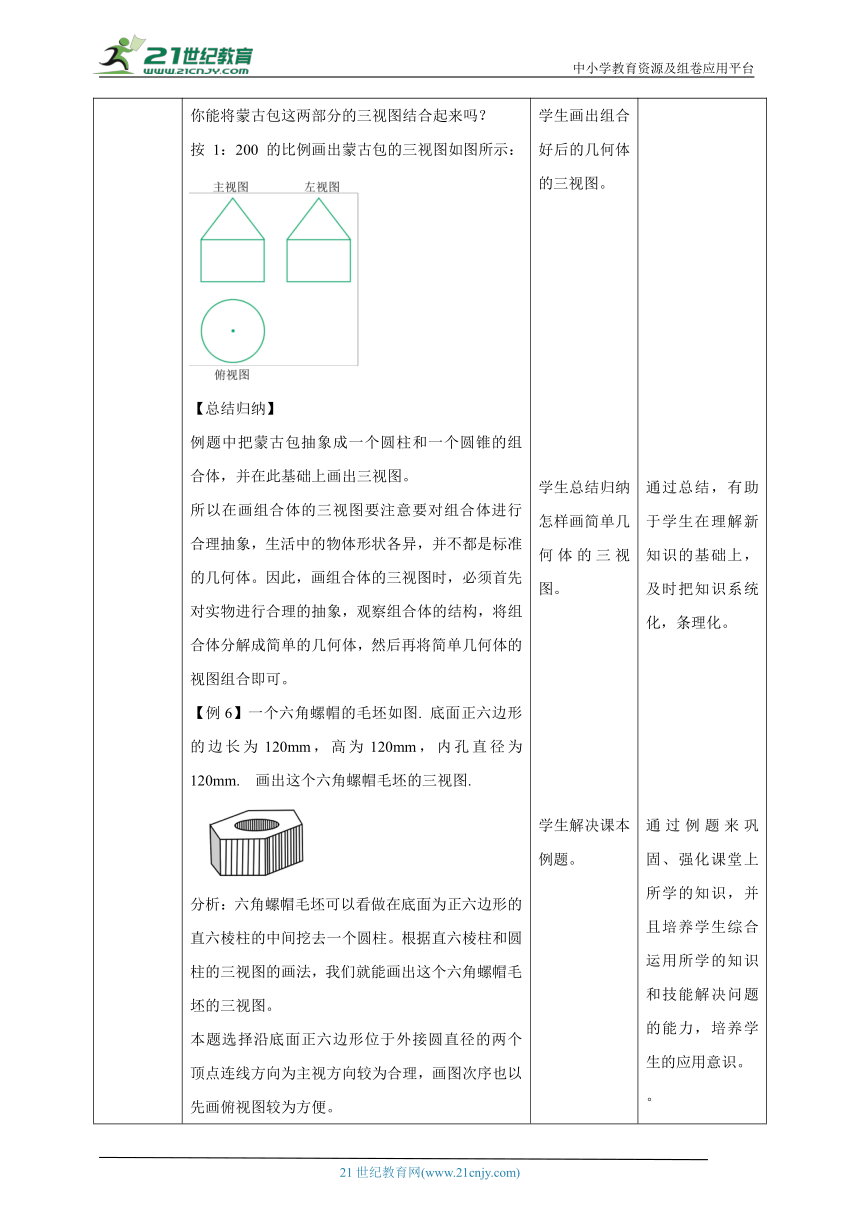
讲授新课 【例5】一个蒙古包如图,它上部的圆锥部分和下部的圆柱部分的高都是2m,底面直径为3m. 以 1 : 200 的比例画出它的三视图.分析:我们可以把蒙古包看成圆柱和圆锥两种几何体的组合体. 利用三视图的正投影原理,想象出蒙古包在正投影面、水平投影面、侧投影面上的正投影的图形,就可画出三视图.你能按照按 1 : 200 的比例画出蒙古包上部的圆锥部分的三视图吗?按照比例计算,圆锥的高为1cm,圆锥的底面直径为1.5cm,所以圆锥的三视图如图所示:你能按照按 1 : 200 的比例画出蒙古包下部的圆柱部分的三视图吗?按照比例计算,圆柱的高为1cm,圆柱的底面直径为1.5cm,所以圆柱的三视图如图所示:你能将蒙古包这两部分的三视图结合起来吗?按 1:200 的比例画出蒙古包的三视图如图所示:【总结归纳】例题中把蒙古包抽象成一个圆柱和一个圆锥的组合体,并在此基础上画出三视图。所以在画组合体的三视图要注意要对组合体进行合理抽象,生活中的物体形状各异,并不都是标准的几何体。因此,画组合体的三视图时,必须首先对实物进行合理的抽象,观察组合体的结构,将组合体分解成简单的几何体,然后再将简单几何体的视图组合即可。【例6】一个六角螺帽的毛坯如图. 底面正六边形的边长为120mm,高为120mm,内孔直径为 120mm. 画出这个六角螺帽毛坯的三视图.分析:六角螺帽毛坯可以看做在底面为正六边形的直六棱柱的中间挖去一个圆柱。根据直六棱柱和圆柱的三视图的画法,我们就能画出这个六角螺帽毛坯的三视图。本题选择沿底面正六边形位于外接圆直径的两个顶点连线方向为主视方向较为合理,画图次序也以先画俯视图较为方便。解:选取1:10的比例,画出这个六角螺帽毛坯的三视图,如图所示.【总结归纳】画简单的组合体的三视图方法:把简单的组合体的视图,分解成若干部分,分别想象出各部分的几何体,综合后描述出几何体的全貌。注意:画视图时,看得见部分的轮廓线画成实线,看不见部分的轮廓线画成虚线。 学生探究怎样画组合图形的三视图。学生将组合图形拆解画出拆解后的三视图。学生画出组合好后的几何体的三视图。学生总结归纳怎样画简单几何体的三视图。学生解决课本例题。 在教学中运用探究式教学模式,使学生体验教学再创造的思维过程,培养学生的创造意识和科学精神。通过多媒体直观的演示,学生能够直观具体的体会组合体和简单结合体之间的联系与区别。通过总结,有助于学生在理解新知识的基础上,及时把知识系统化,条理化。通过例题来巩固、强化课堂上所学的知识,并且培养学生综合运用所学的知识和技能解决问题的能力,培养学生的应用意识。。
课堂练习 1.如图是由一个圆柱体和一个长方体组成的几何体,其左视图是( A )2.如图所示的几何体是六角螺栓,其俯视图是( A )3.如图是由4个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体与原几何体相比,( C )A.主视图改变,左视图改变B.俯视图不变,左视图改变C.俯视图改变,左视图改变D.主视图不变,左视图不变4.如图是由5个小正方体组合成的几何体,则其俯视图为( A )5.下图是由一个长方体和一个圆锥组成的几何体,它的主视图是( C ).6.如图是一个粮仓,其顶部是一个圆锥,底部是一个圆柱.画出这个粮仓的三视图;解:如图所示: 学生做练习,教师订正答案。 通过各种形式的练习,进一步提高学生学习兴趣,使 学生的认知结构更加完善。同时强化本课的教学重点,突破教学难点。
课堂小结 本节课你学到了什么?怎样画简单的组合体的三视图?方法:把简单的组合体的视图,分解成若干部分,分别想象出各部分的几何体,综合后描述出几何体的全貌。注意:画视图时,看得见部分的轮廓线画成实线,看不见部分的轮廓线画成虚线。 学生总结本节课学习的内容。 充分发挥学生的主体作用,有助于学生在理解新知识的基础上,及时把知识系统化,条理化。
板书 课题:3.2简单几何体的三视图(3) 一、画简单几何体的三视图二、例题讲解
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
浙教版九年级下册数学3.2简单几何体的三视图(3) 教学设计
课题 3.2简单几何体的三视图(3) 单元 第3单元 学科 数学 年级 九
教材分析 本节内容是浙教版九年级下册数学3.2简单几何体的三视图第3课时的内容。从第3节的整体来看,是本章的重点部分,是培养空间想象能力和读图能力的关键一章,起着承上启下的作用,本节课着重培养学生分析和解决问题的能力。本节课是在前面已学过画单独图形的三视图之后的一节比较综合的新授课,对于同学们空间思维能力和空间想象能力也会有较大的提升。
核心素养分析 本节课通过有趣的提问和动手实践激发学生的学习兴趣,利用多媒体动画课件直观生动的讲解,降低学习难度,增强学生学习自信心,变被动学习为主动学习,有利于掌握知识,培养学生自主分析判断问题、解决问题的能力,培养学生达到一定的语言表达能力。
学习目标 1.能够根据不同的物体,学会判断组合体的类型,分析选择主视图,并画出三视图。2.通过画、量、讲等各种学习形式,进一步提高学生的绘图能力,提高空间思维和空间想象能力。3.通过进一步熟悉画三视图,培养协作能力和团队精神,树立科学严谨的学习态度。
重点 通过对组合体形状分析,会画组合体的三视图。
难点 通过“分”“合”的方法,将图形化繁为简,单独画出基本体的三个视图,再将所有基本体组合起来。
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 你能说一说圆柱和圆锥的三视图是什么形状吗?1.圆柱的主视图、左视图是矩形,矩形的一边长是圆柱的高,一边长是圆柱底面圆的直径,圆柱的俯视图是圆。2.圆锥的主视图、左视图是等腰三角形,三角形的高线长是圆锥的高,底边长是圆锥底面圆的直径,圆锥的俯视图是圆。同学们见过蒙古包吗?蒙古包是什么形状的?如图所示的蒙古包的上部是圆锥,下部是圆柱。我们怎样用平面图形去表示蒙古包的形状和大小呢? 学生思考回答问题,复习会议圆柱和圆锥的三视图。 通过复习,激发学生学习动机和兴趣,吸引学生注意力,为引进新知识的学习做好心理准备。
讲授新课 【例5】一个蒙古包如图,它上部的圆锥部分和下部的圆柱部分的高都是2m,底面直径为3m. 以 1 : 200 的比例画出它的三视图.分析:我们可以把蒙古包看成圆柱和圆锥两种几何体的组合体. 利用三视图的正投影原理,想象出蒙古包在正投影面、水平投影面、侧投影面上的正投影的图形,就可画出三视图.你能按照按 1 : 200 的比例画出蒙古包上部的圆锥部分的三视图吗?按照比例计算,圆锥的高为1cm,圆锥的底面直径为1.5cm,所以圆锥的三视图如图所示:你能按照按 1 : 200 的比例画出蒙古包下部的圆柱部分的三视图吗?按照比例计算,圆柱的高为1cm,圆柱的底面直径为1.5cm,所以圆柱的三视图如图所示:你能将蒙古包这两部分的三视图结合起来吗?按 1:200 的比例画出蒙古包的三视图如图所示:【总结归纳】例题中把蒙古包抽象成一个圆柱和一个圆锥的组合体,并在此基础上画出三视图。所以在画组合体的三视图要注意要对组合体进行合理抽象,生活中的物体形状各异,并不都是标准的几何体。因此,画组合体的三视图时,必须首先对实物进行合理的抽象,观察组合体的结构,将组合体分解成简单的几何体,然后再将简单几何体的视图组合即可。【例6】一个六角螺帽的毛坯如图. 底面正六边形的边长为120mm,高为120mm,内孔直径为 120mm. 画出这个六角螺帽毛坯的三视图.分析:六角螺帽毛坯可以看做在底面为正六边形的直六棱柱的中间挖去一个圆柱。根据直六棱柱和圆柱的三视图的画法,我们就能画出这个六角螺帽毛坯的三视图。本题选择沿底面正六边形位于外接圆直径的两个顶点连线方向为主视方向较为合理,画图次序也以先画俯视图较为方便。解:选取1:10的比例,画出这个六角螺帽毛坯的三视图,如图所示.【总结归纳】画简单的组合体的三视图方法:把简单的组合体的视图,分解成若干部分,分别想象出各部分的几何体,综合后描述出几何体的全貌。注意:画视图时,看得见部分的轮廓线画成实线,看不见部分的轮廓线画成虚线。 学生探究怎样画组合图形的三视图。学生将组合图形拆解画出拆解后的三视图。学生画出组合好后的几何体的三视图。学生总结归纳怎样画简单几何体的三视图。学生解决课本例题。 在教学中运用探究式教学模式,使学生体验教学再创造的思维过程,培养学生的创造意识和科学精神。通过多媒体直观的演示,学生能够直观具体的体会组合体和简单结合体之间的联系与区别。通过总结,有助于学生在理解新知识的基础上,及时把知识系统化,条理化。通过例题来巩固、强化课堂上所学的知识,并且培养学生综合运用所学的知识和技能解决问题的能力,培养学生的应用意识。。
课堂练习 1.如图是由一个圆柱体和一个长方体组成的几何体,其左视图是( A )2.如图所示的几何体是六角螺栓,其俯视图是( A )3.如图是由4个同样大小的正方体摆成的几何体,将正方体①移走后,所得几何体与原几何体相比,( C )A.主视图改变,左视图改变B.俯视图不变,左视图改变C.俯视图改变,左视图改变D.主视图不变,左视图不变4.如图是由5个小正方体组合成的几何体,则其俯视图为( A )5.下图是由一个长方体和一个圆锥组成的几何体,它的主视图是( C ).6.如图是一个粮仓,其顶部是一个圆锥,底部是一个圆柱.画出这个粮仓的三视图;解:如图所示: 学生做练习,教师订正答案。 通过各种形式的练习,进一步提高学生学习兴趣,使 学生的认知结构更加完善。同时强化本课的教学重点,突破教学难点。
课堂小结 本节课你学到了什么?怎样画简单的组合体的三视图?方法:把简单的组合体的视图,分解成若干部分,分别想象出各部分的几何体,综合后描述出几何体的全貌。注意:画视图时,看得见部分的轮廓线画成实线,看不见部分的轮廓线画成虚线。 学生总结本节课学习的内容。 充分发挥学生的主体作用,有助于学生在理解新知识的基础上,及时把知识系统化,条理化。
板书 课题:3.2简单几何体的三视图(3) 一、画简单几何体的三视图二、例题讲解
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
