【核心素养目标】3.3由三视图描述几何体 教学设计
文档属性
| 名称 | 【核心素养目标】3.3由三视图描述几何体 教学设计 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-01 14:05:46 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
浙教版九年级下册数学3.3由三视图描述几何体教学设计
课题 3.3由三视图描述几何体 单元 第3单元 学 科 数学 年级 九
教材分析 本节课教学内容是浙教版九年级下册数学3.3由三视图描述几何体。三视图在整个初中课程和中考都占有重要地位。《三视图》的知识与我们日常生活、生产、科学研究等领域有着密切的联系,因此学习这部分内容有着广泛的现实意义。由三视图还原成实物图是培养学生空间想象能力的重要载体,为后面立体几何的学习做了一个很好的铺垫,同时它也是许多知识的载体,如计算几何体的体积或表面积等。所以三视图的还原对整个立体几何的学习有深刻影响,起着承上启下的作用,要引起足够重视。
核心素养分析 通过观察探究等活动使学生能根据物体的三视图还原出物体的形状,进一步认识物体与其三视图之间的关系,让学生体验数、符号和图形是有效地描述现实世界的重要手段,从而获取立体图形的实感,逐步培养学生的空间想象能力,同时在探究三视图向立体图形转换的过程中,使学生感受到数学的和谐美、奇艺美。
学习目标 1.学会根据物体的三视图描述出几何体的基本形状或实物原型.2.经历探索简单的几何体的三视图的还原,进一步发展空间想象能力.3.通过引导探究,启发在学习中探索的意识,培养善用技巧解决问题的能力。
重点 学会根据物体的三视图描述出几何体的基本形状或实物原型.
难点 理解三视图转化为立体图的过程.
教学过程
教学环节 教师活动 学生活动 设计意图
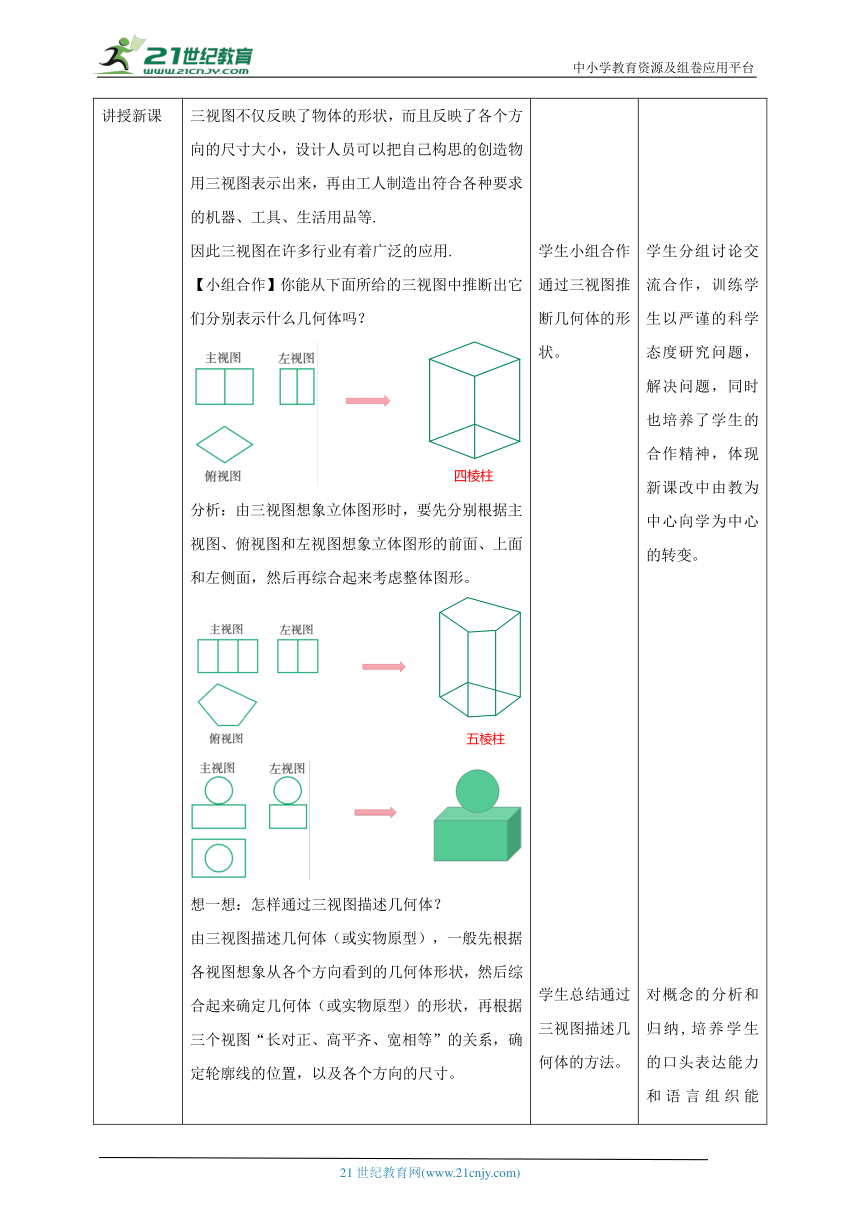
导入新课 【思考】怎样画一个几何体的三视图?画三视图时,三个视图要放在正确的位置,并且使主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等;画图时规定:看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.【想一想】你能通过一个物体的三视图画出这个物体的形状吗?例如根据三视图,工人就能制造出符合设计要求的零件. 学生思考回答问题。 通过完成自主预习任务,让学生回顾三视图的部分知识,为本节课的内容做铺垫,同时引入本节课的探究内容。
讲授新课 三视图不仅反映了物体的形状,而且反映了各个方向的尺寸大小,设计人员可以把自己构思的创造物用三视图表示出来,再由工人制造出符合各种要求的机器、工具、生活用品等. 因此三视图在许多行业有着广泛的应用.【小组合作】你能从下面所给的三视图中推断出它们分别表示什么几何体吗?分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形。想一想:怎样通过三视图描述几何体?由三视图描述几何体(或实物原型),一般先根据各视图想象从各个方向看到的几何体形状,然后综合起来确定几何体(或实物原型)的形状,再根据三个视图“长对正、高平齐、宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸。【总结归纳】由三视图描述几何体可以从如下几个方面进行分析:(1)根据主视图、俯视图和左视图想象从各个方向看到的几何体形状,然后综合起来确定几何体的形状和大小;(2)根据实线、虚线想象几何体看得见和看不见的轮廓线;(3)由简单几何体的三视图想象复杂几何体的形状。【例】已知一个几何体的三视图如图所示,描述该几何体的形状,量出三视图的有关尺寸,并根据已知的比例求出它的侧面积(精确到0.1cm2)分析:由主视图和左视图知道,这个几何体是直棱柱,但不能确定棱的条数,再由俯视图可以确定它是直四棱柱,且底面是梯形.解:这个几何体是底面为梯形的直四棱柱。量出有关尺寸,根据比例1:3,可得这个直四棱柱各个方向的尺寸.它的四个侧面都是长为9cm的长方形,前侧面的宽为3cm,后侧面的宽为6cm,左侧面的宽为4.5cm.由勾股定理,可得右侧面的宽为 所以它的侧面积为3×9+6×9+4.5×9+×9≈170.2(cm2)。答:这个几何体的侧面积为170.2cm2. 学生小组合作通过三视图推断几何体的形状。学生总结通过三视图描述几何体的方法。学生根据所学知识做课本例题。 学生分组讨论交流合作,训练学生以严谨的科学态度研究问题,解决问题,同时也培养了学生的合作精神,体现新课改中由教为中心向学为中心的转变。对概念的分析和归纳,培养学生的口头表达能力和语言组织能力,同时渗透类比思想.通过例题来巩固、强化课堂上所学的知识,并且培养学生综合运用所学的知识和技能解决问题的能力,培养学生的应用意识。
课堂练习 1.如图是一个几何体的三视图,这个几何体是( D )A.圆锥 B.长方体 C.球 D.圆柱2.某个几何体的三视图如图所示,该几何体是(A)3.一个几何体的三视图如图所示,这个几何体可能是( C )4.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( B ).A.108 cm3 B.100 cm3C.92 cm3 D.84 cm35.如图是一个组合几何体的两种视图.(单位:cm)(1)请写出这个组合几何体是由哪两种几何体组成的;解:这个组合几何体是由圆柱与长方体组成的.(2)计算这个组合几何体的体积(结果保留π).解:由题意,得组合几何体的体积=圆柱体积+长方体体积,即6π×+8×5×2=24π+80(cm3).答:这个组合几何体的体积为(24π+80) cm3 学生做练习,教师订正答案。 通过各种形式的练习,进一步提高学生学习兴趣,使 学生的认知结构更加完善。同时强化本课的教学重点,突破教学难点。
课堂小结 本节课你学到了什么?通过三视图推断几何体的形状。由三视图描述几何体(或实物原型),一般先根据各视图想象从各个方向看到的几何体形状,然后综合起来确定几何体(或实物原型)的形状,再根据三个视图“长对正、高平齐、宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸 学生总结归纳。
板书 课题:3.3由三视图描述几何体一、由三视图描述几何体二、解决问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
浙教版九年级下册数学3.3由三视图描述几何体教学设计
课题 3.3由三视图描述几何体 单元 第3单元 学 科 数学 年级 九
教材分析 本节课教学内容是浙教版九年级下册数学3.3由三视图描述几何体。三视图在整个初中课程和中考都占有重要地位。《三视图》的知识与我们日常生活、生产、科学研究等领域有着密切的联系,因此学习这部分内容有着广泛的现实意义。由三视图还原成实物图是培养学生空间想象能力的重要载体,为后面立体几何的学习做了一个很好的铺垫,同时它也是许多知识的载体,如计算几何体的体积或表面积等。所以三视图的还原对整个立体几何的学习有深刻影响,起着承上启下的作用,要引起足够重视。
核心素养分析 通过观察探究等活动使学生能根据物体的三视图还原出物体的形状,进一步认识物体与其三视图之间的关系,让学生体验数、符号和图形是有效地描述现实世界的重要手段,从而获取立体图形的实感,逐步培养学生的空间想象能力,同时在探究三视图向立体图形转换的过程中,使学生感受到数学的和谐美、奇艺美。
学习目标 1.学会根据物体的三视图描述出几何体的基本形状或实物原型.2.经历探索简单的几何体的三视图的还原,进一步发展空间想象能力.3.通过引导探究,启发在学习中探索的意识,培养善用技巧解决问题的能力。
重点 学会根据物体的三视图描述出几何体的基本形状或实物原型.
难点 理解三视图转化为立体图的过程.
教学过程
教学环节 教师活动 学生活动 设计意图
导入新课 【思考】怎样画一个几何体的三视图?画三视图时,三个视图要放在正确的位置,并且使主视图与俯视图的长对正,主视图与左视图的高平齐,左视图与俯视图的宽相等;画图时规定:看得见部分的轮廓线画成实线,因被其他部分遮挡而看不见部分的轮廓线画成虚线.【想一想】你能通过一个物体的三视图画出这个物体的形状吗?例如根据三视图,工人就能制造出符合设计要求的零件. 学生思考回答问题。 通过完成自主预习任务,让学生回顾三视图的部分知识,为本节课的内容做铺垫,同时引入本节课的探究内容。
讲授新课 三视图不仅反映了物体的形状,而且反映了各个方向的尺寸大小,设计人员可以把自己构思的创造物用三视图表示出来,再由工人制造出符合各种要求的机器、工具、生活用品等. 因此三视图在许多行业有着广泛的应用.【小组合作】你能从下面所给的三视图中推断出它们分别表示什么几何体吗?分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形。想一想:怎样通过三视图描述几何体?由三视图描述几何体(或实物原型),一般先根据各视图想象从各个方向看到的几何体形状,然后综合起来确定几何体(或实物原型)的形状,再根据三个视图“长对正、高平齐、宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸。【总结归纳】由三视图描述几何体可以从如下几个方面进行分析:(1)根据主视图、俯视图和左视图想象从各个方向看到的几何体形状,然后综合起来确定几何体的形状和大小;(2)根据实线、虚线想象几何体看得见和看不见的轮廓线;(3)由简单几何体的三视图想象复杂几何体的形状。【例】已知一个几何体的三视图如图所示,描述该几何体的形状,量出三视图的有关尺寸,并根据已知的比例求出它的侧面积(精确到0.1cm2)分析:由主视图和左视图知道,这个几何体是直棱柱,但不能确定棱的条数,再由俯视图可以确定它是直四棱柱,且底面是梯形.解:这个几何体是底面为梯形的直四棱柱。量出有关尺寸,根据比例1:3,可得这个直四棱柱各个方向的尺寸.它的四个侧面都是长为9cm的长方形,前侧面的宽为3cm,后侧面的宽为6cm,左侧面的宽为4.5cm.由勾股定理,可得右侧面的宽为 所以它的侧面积为3×9+6×9+4.5×9+×9≈170.2(cm2)。答:这个几何体的侧面积为170.2cm2. 学生小组合作通过三视图推断几何体的形状。学生总结通过三视图描述几何体的方法。学生根据所学知识做课本例题。 学生分组讨论交流合作,训练学生以严谨的科学态度研究问题,解决问题,同时也培养了学生的合作精神,体现新课改中由教为中心向学为中心的转变。对概念的分析和归纳,培养学生的口头表达能力和语言组织能力,同时渗透类比思想.通过例题来巩固、强化课堂上所学的知识,并且培养学生综合运用所学的知识和技能解决问题的能力,培养学生的应用意识。
课堂练习 1.如图是一个几何体的三视图,这个几何体是( D )A.圆锥 B.长方体 C.球 D.圆柱2.某个几何体的三视图如图所示,该几何体是(A)3.一个几何体的三视图如图所示,这个几何体可能是( C )4.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是( B ).A.108 cm3 B.100 cm3C.92 cm3 D.84 cm35.如图是一个组合几何体的两种视图.(单位:cm)(1)请写出这个组合几何体是由哪两种几何体组成的;解:这个组合几何体是由圆柱与长方体组成的.(2)计算这个组合几何体的体积(结果保留π).解:由题意,得组合几何体的体积=圆柱体积+长方体体积,即6π×+8×5×2=24π+80(cm3).答:这个组合几何体的体积为(24π+80) cm3 学生做练习,教师订正答案。 通过各种形式的练习,进一步提高学生学习兴趣,使 学生的认知结构更加完善。同时强化本课的教学重点,突破教学难点。
课堂小结 本节课你学到了什么?通过三视图推断几何体的形状。由三视图描述几何体(或实物原型),一般先根据各视图想象从各个方向看到的几何体形状,然后综合起来确定几何体(或实物原型)的形状,再根据三个视图“长对正、高平齐、宽相等”的关系,确定轮廓线的位置,以及各个方向的尺寸 学生总结归纳。
板书 课题:3.3由三视图描述几何体一、由三视图描述几何体二、解决问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
