2.3一元二次方程的应用(1) 课件(共14张PPT)
文档属性
| 名称 | 2.3一元二次方程的应用(1) 课件(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1022.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-02-28 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
浙教版八下数学
2.3 一元二次方程的应用 (1)
设基数为a,平均增长率为x,则一次增长后的值为
设基数为a,平均降低率为x,则一次降低后的值为
温故知新:
a(1+x)
a(1+x)2
a(1+x)n
a(1-x)
a(1-x)2
a(1-x)n
(1)
平均增长率中的数量关系
(2)
平均降低率中的数量关系:
依次类推n次增长后的值为
二次增长后的值为
二次降低后的值为
依次类推n次降低后的值为
递增递减问题
学以致用:
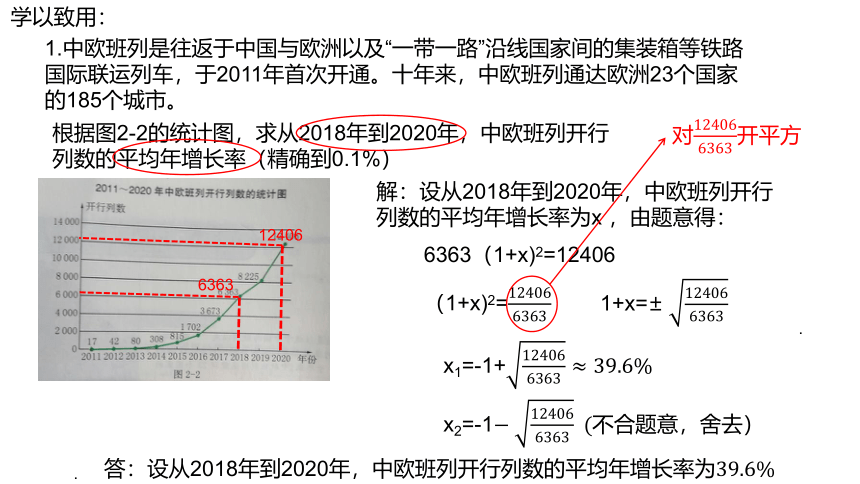
1.中欧班列是往返于中国与欧洲以及“一带一路”沿线国家间的集装箱等铁路国际联运列车,于2011年首次开通。十年来,中欧班列通达欧洲23个国家的185个城市。
根据图2-2的统计图,求从2018年到2020年,中欧班列开行列数的平均年增长率(精确到0.1%)
6363
12406
解:设从2018年到2020年,中欧班列开行列数的平均年增长率为x ,由题意得:
6363(1+x)2=12406
(1+x)2=
.
1+x=
.
x1=-1+
x2=-1
.
答:设从2018年到2020年,中欧班列开行列数的平均年增长率为
.
对开平方
总利润=_________________________
1. 总利润=_______________
总售价-总成本
每件商品的利润×总销售量
温故知新:
销售问题
2. 利润率=
.
3. 售价=
.
10
售价:进价
.
株数
平均每株盈利
每盆盈利
… … …
3
3
3×3
增加1株
3+1
增加2株
3+2
3-0.5×2
增加x株
3+x
3-0.5x
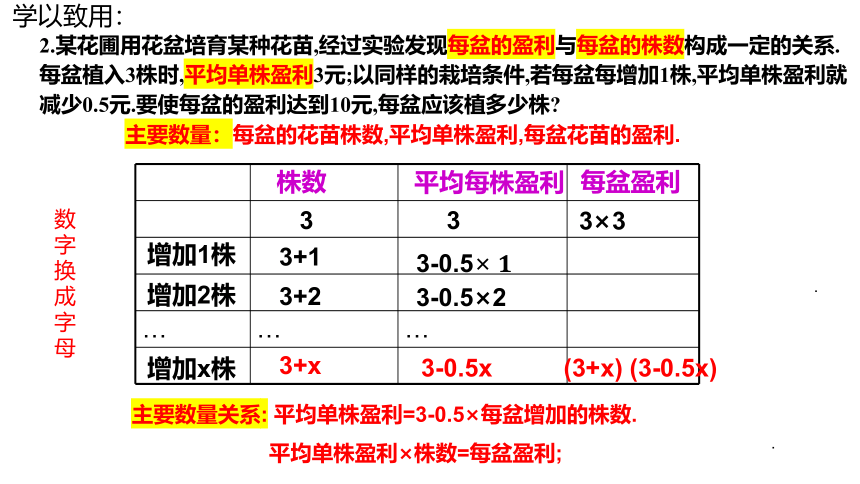
2.某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株
(3+x)
(3-0.5x)
主要数量:每盆的花苗株数,平均单株盈利,每盆花苗的盈利.
学以致用:
主要数量关系: 平均单株盈利=3-0.5×每盆增加的株数.
平均单株盈利×株数=每盆盈利;
.
3-0.5
.
数字换成字母
1.某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株
解:法1.设每盆花苗增加x株,
(x+3) (3-0.5x)=10
化简,整理,得 x2-3x+2=0
解这个方程,得 x1=1,x2=2.
经检验,x1=1,x2=2都是方程的解,且符合题意.
答:要使每盆的盈利达到10元,每盆应植入4株或5株.
平均单株盈利=______________元,由题意得.
则每盆增加的株数=_______株,
(x-3)
[3-0.5(x-3)]
x[3-0.5(x-3)]=10
化简,整理,得 x2-9x+20=0,
解这个方程,得 x1=4,x2=5.
间接设法
直接设法
则每盆花苗有(3+x)株,平均单株盈利为(3-0.5x)元.由题意得:
法2.设每盆植x株
每盆花苗有4株或5株
解:设较小的一个奇数为x,则另一个数为x+2.
根据题意列方程得:x(x+2)=143
解得:x1=11,x2=-13
经检验,x2=-13不符合题意,舍去。
答:这两个数奇数是11和13.
当堂检测:
夯实基础,稳扎稳打
:x2+2x=143
:x2+2x+1=143+1
:(x+1)2=144
x+1=
.
1.已知两个连续正奇数的积等于143,应用一元二次方程求这两个数.
.
x+1=12
.
2.有一人患了流感,经过两轮传染后共有100人患了流感,每轮传染中平均一个人传染了几个人 画树状图。
分析:设每轮传染中平均一个人传染了x个人. 传染源记作小明,其传染示意图如下:
第2轮
第2轮传染后共有人数:
x(x+1)+x+1=(x+1)2
小明
第1轮
小明
第1轮传染后共有人数: x+1
1
2
x
分析:设每轮传染中平均一个人传染了x 个人.
(1+x)2=100
解方程,得
x1= , x2=
9
-11
(不合题意,舍去).
4 轮传染后,共有传染的人数:
(1+9)4=104>7000.
若不隔离,经过4 轮传染后,共有传染的人数会不会超过 7000 人?
3.某超市销售一种饮料,平均每天可售出100箱,每箱利润12元.为了扩大销售,增加利润,超市准备适当降价.据测算,若每箱降价1元,每天可多售出20箱.如果要使每天销售饮料获利1400元,问每箱应降价多少元?
数量关系是:
销售每箱饮料的利润×销售总箱数=销售总利润
解:设要使每天销售饮料获利1400元,每箱应降价x元,依据题意列方程得,
(12-x)(100+20x)=1400,
整理得x2-7x+10=0, 解得x1=2,x2=5;
答:每箱应降价2元或5元,可使每天销售饮料获利14000元
4.某校坚持对学生进行近视眼的防治,近视学生人数逐年减少.据统计,今年的近视学生人数是前年人数的75℅,那么这两年平均每年近视学生人数降低的百分率是多少(精确到1℅)
(1-x)2=0.75
提示:增长率问题中若基数不明确,通常设为“1”,或设为a等
设为“1”:
设为“a”:
x1=1-
x2=1
(1-x)2a=0.75a
.
前年人数为a,今年人数为0.75a
5.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是21,每个支干长出多少小分支
支干
x
主干
1
支干
……
……
小分支
……
小分支
x
x
分析:设每个支干长出x个小分支,得:
1+x+x2=21
画树状图:
x2+x-20=0
(x+5)(x-4)=0
x1=-5(舍去), x2=4
小分支
小分支
……
连续递推,豁然开朗
每天的销售量/台 每台的销售利润/元 总销售利润/元
降价前
降价后
列出方程:
分析:如果设每台冰箱降价x元,那么每台冰箱的定价应为 ________元.
( 8+4× )( 2900-x-2500 ) = 5000
(2900-x)
6.某商场销售某种冰箱,每台进货价为2500元.调查发现,当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
化简,得 x2-300x+22500=0
x1=x2=150
∴2900-x=2900-150=2750
8
2900-2500
3200
8+4×
2900-2500-x
5000
化“1”: 每降低1元:
多售出台
.
7. 某批发市场礼品柜台春节期间购进大量贺年卡,一种贺年卡平均每天可售出 500 张,每张赢利 0.3 元. 为了尽快减少库存,摊主决定采取适当的降价措施.调查发现,如果这种贺年卡的售价每降价 0.05 元,那么平均每天可多售出 200 张. 摊主要想平均每天赢利 180 元,每张贺年卡应降价多少元?
解:设每张贺年卡应降价x元,则现在的利润是(0.3-x)元,多售出200x÷0.05=4 000x(张).
根据题意,得(0.3-x)(500+4 000x)=180,
整理,得400x2-70x+3=0.解得x1= ,x2=0.1.
∵为了尽快减少库存,∴x=0.1.
答:每张贺年卡应降价0.1元.
化“1”: 每降低1元:
多售出 4000 张
8、一个容器内盛满纯酒精50L,每一次倒出一部分纯酒精后用水加满;第二次又倒出同样多的酒精溶液,再用水加满,这时容器中的酒精溶液含酒精32L。求每次倒出溶液的升数。
解:设每次倒出溶液x升,由题意得:
(1-=
.
50(1-=32
.
(1-=
.
1-=
.
1-=- (舍去)
.
x=10
答:每次倒出溶液10升
思维拓展,更上一层楼
浙教版八下数学
2.3 一元二次方程的应用 (1)
设基数为a,平均增长率为x,则一次增长后的值为
设基数为a,平均降低率为x,则一次降低后的值为
温故知新:
a(1+x)
a(1+x)2
a(1+x)n
a(1-x)
a(1-x)2
a(1-x)n
(1)
平均增长率中的数量关系
(2)
平均降低率中的数量关系:
依次类推n次增长后的值为
二次增长后的值为
二次降低后的值为
依次类推n次降低后的值为
递增递减问题
学以致用:
1.中欧班列是往返于中国与欧洲以及“一带一路”沿线国家间的集装箱等铁路国际联运列车,于2011年首次开通。十年来,中欧班列通达欧洲23个国家的185个城市。
根据图2-2的统计图,求从2018年到2020年,中欧班列开行列数的平均年增长率(精确到0.1%)
6363
12406
解:设从2018年到2020年,中欧班列开行列数的平均年增长率为x ,由题意得:
6363(1+x)2=12406
(1+x)2=
.
1+x=
.
x1=-1+
x2=-1
.
答:设从2018年到2020年,中欧班列开行列数的平均年增长率为
.
对开平方
总利润=_________________________
1. 总利润=_______________
总售价-总成本
每件商品的利润×总销售量
温故知新:
销售问题
2. 利润率=
.
3. 售价=
.
10
售价:进价
.
株数
平均每株盈利
每盆盈利
… … …
3
3
3×3
增加1株
3+1
增加2株
3+2
3-0.5×2
增加x株
3+x
3-0.5x
2.某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株
(3+x)
(3-0.5x)
主要数量:每盆的花苗株数,平均单株盈利,每盆花苗的盈利.
学以致用:
主要数量关系: 平均单株盈利=3-0.5×每盆增加的株数.
平均单株盈利×株数=每盆盈利;
.
3-0.5
.
数字换成字母
1.某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3元;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株
解:法1.设每盆花苗增加x株,
(x+3) (3-0.5x)=10
化简,整理,得 x2-3x+2=0
解这个方程,得 x1=1,x2=2.
经检验,x1=1,x2=2都是方程的解,且符合题意.
答:要使每盆的盈利达到10元,每盆应植入4株或5株.
平均单株盈利=______________元,由题意得.
则每盆增加的株数=_______株,
(x-3)
[3-0.5(x-3)]
x[3-0.5(x-3)]=10
化简,整理,得 x2-9x+20=0,
解这个方程,得 x1=4,x2=5.
间接设法
直接设法
则每盆花苗有(3+x)株,平均单株盈利为(3-0.5x)元.由题意得:
法2.设每盆植x株
每盆花苗有4株或5株
解:设较小的一个奇数为x,则另一个数为x+2.
根据题意列方程得:x(x+2)=143
解得:x1=11,x2=-13
经检验,x2=-13不符合题意,舍去。
答:这两个数奇数是11和13.
当堂检测:
夯实基础,稳扎稳打
:x2+2x=143
:x2+2x+1=143+1
:(x+1)2=144
x+1=
.
1.已知两个连续正奇数的积等于143,应用一元二次方程求这两个数.
.
x+1=12
.
2.有一人患了流感,经过两轮传染后共有100人患了流感,每轮传染中平均一个人传染了几个人 画树状图。
分析:设每轮传染中平均一个人传染了x个人. 传染源记作小明,其传染示意图如下:
第2轮
第2轮传染后共有人数:
x(x+1)+x+1=(x+1)2
小明
第1轮
小明
第1轮传染后共有人数: x+1
1
2
x
分析:设每轮传染中平均一个人传染了x 个人.
(1+x)2=100
解方程,得
x1= , x2=
9
-11
(不合题意,舍去).
4 轮传染后,共有传染的人数:
(1+9)4=104>7000.
若不隔离,经过4 轮传染后,共有传染的人数会不会超过 7000 人?
3.某超市销售一种饮料,平均每天可售出100箱,每箱利润12元.为了扩大销售,增加利润,超市准备适当降价.据测算,若每箱降价1元,每天可多售出20箱.如果要使每天销售饮料获利1400元,问每箱应降价多少元?
数量关系是:
销售每箱饮料的利润×销售总箱数=销售总利润
解:设要使每天销售饮料获利1400元,每箱应降价x元,依据题意列方程得,
(12-x)(100+20x)=1400,
整理得x2-7x+10=0, 解得x1=2,x2=5;
答:每箱应降价2元或5元,可使每天销售饮料获利14000元
4.某校坚持对学生进行近视眼的防治,近视学生人数逐年减少.据统计,今年的近视学生人数是前年人数的75℅,那么这两年平均每年近视学生人数降低的百分率是多少(精确到1℅)
(1-x)2=0.75
提示:增长率问题中若基数不明确,通常设为“1”,或设为a等
设为“1”:
设为“a”:
x1=1-
x2=1
(1-x)2a=0.75a
.
前年人数为a,今年人数为0.75a
5.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是21,每个支干长出多少小分支
支干
x
主干
1
支干
……
……
小分支
……
小分支
x
x
分析:设每个支干长出x个小分支,得:
1+x+x2=21
画树状图:
x2+x-20=0
(x+5)(x-4)=0
x1=-5(舍去), x2=4
小分支
小分支
……
连续递推,豁然开朗
每天的销售量/台 每台的销售利润/元 总销售利润/元
降价前
降价后
列出方程:
分析:如果设每台冰箱降价x元,那么每台冰箱的定价应为 ________元.
( 8+4× )( 2900-x-2500 ) = 5000
(2900-x)
6.某商场销售某种冰箱,每台进货价为2500元.调查发现,当销售价为2900元时,平均每天能售出8台;而当销售价每降低50元时,平均每天就能多售出4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?
化简,得 x2-300x+22500=0
x1=x2=150
∴2900-x=2900-150=2750
8
2900-2500
3200
8+4×
2900-2500-x
5000
化“1”: 每降低1元:
多售出台
.
7. 某批发市场礼品柜台春节期间购进大量贺年卡,一种贺年卡平均每天可售出 500 张,每张赢利 0.3 元. 为了尽快减少库存,摊主决定采取适当的降价措施.调查发现,如果这种贺年卡的售价每降价 0.05 元,那么平均每天可多售出 200 张. 摊主要想平均每天赢利 180 元,每张贺年卡应降价多少元?
解:设每张贺年卡应降价x元,则现在的利润是(0.3-x)元,多售出200x÷0.05=4 000x(张).
根据题意,得(0.3-x)(500+4 000x)=180,
整理,得400x2-70x+3=0.解得x1= ,x2=0.1.
∵为了尽快减少库存,∴x=0.1.
答:每张贺年卡应降价0.1元.
化“1”: 每降低1元:
多售出 4000 张
8、一个容器内盛满纯酒精50L,每一次倒出一部分纯酒精后用水加满;第二次又倒出同样多的酒精溶液,再用水加满,这时容器中的酒精溶液含酒精32L。求每次倒出溶液的升数。
解:设每次倒出溶液x升,由题意得:
(1-=
.
50(1-=32
.
(1-=
.
1-=
.
1-=- (舍去)
.
x=10
答:每次倒出溶液10升
思维拓展,更上一层楼
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
