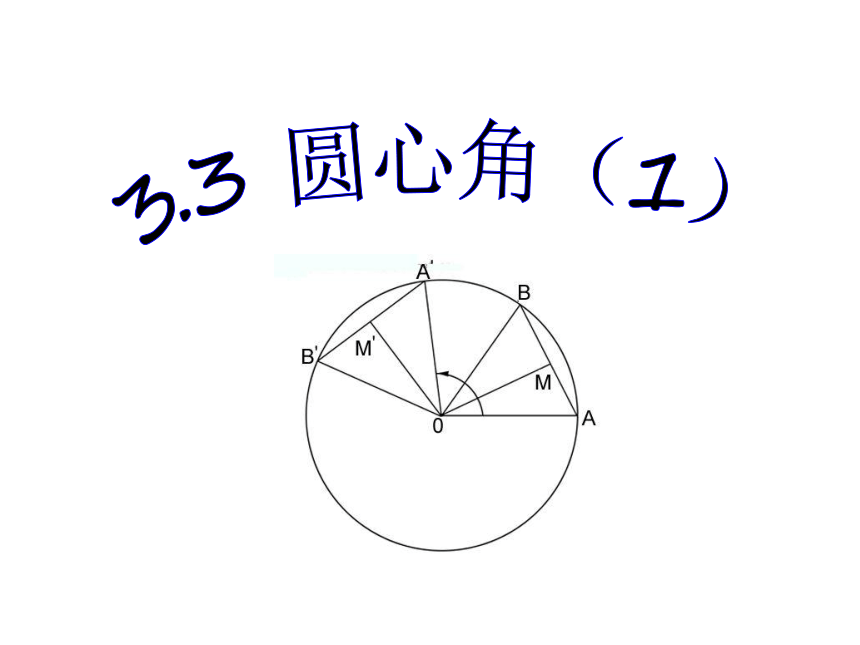
3.3圆心角（1）

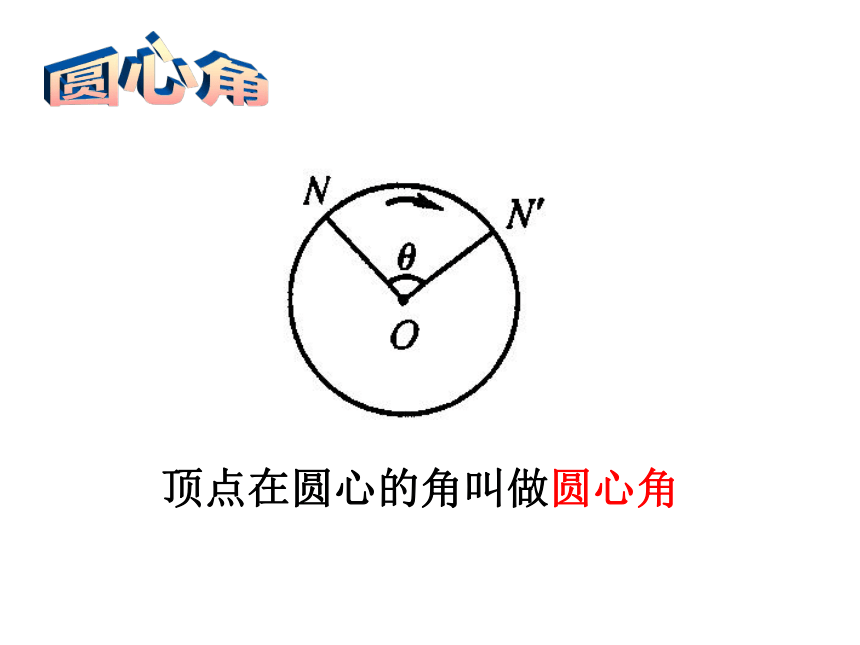
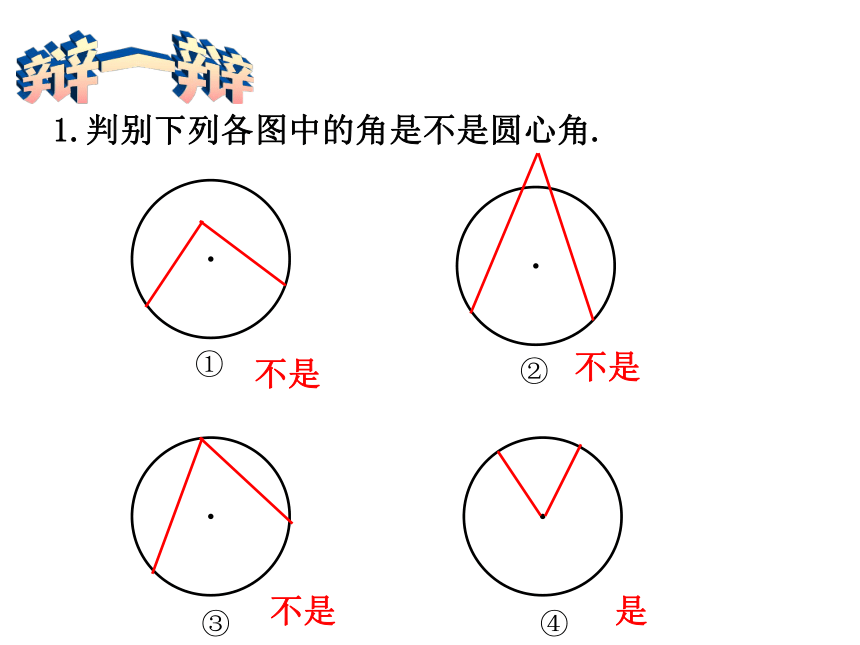
课件30张PPT。探究一1.将一个圆绕圆心旋转180°,所得的像与原图形重合吗？ 2.将圆绕圆心旋转任意角度,所得的像与原图形重合吗？结论：圆是中心对称图形，圆心是它的对称中心．结论：圆具有旋转不变性.圆心角顶点在圆心的角叫做圆心角3.3 圆心角（1）1.判别下列各图中的角是不是圆心角.①②③④辩一辩不是不是不是是2.如图，CD是⊙O的直径，过点D的弦DE平行于半径OA，
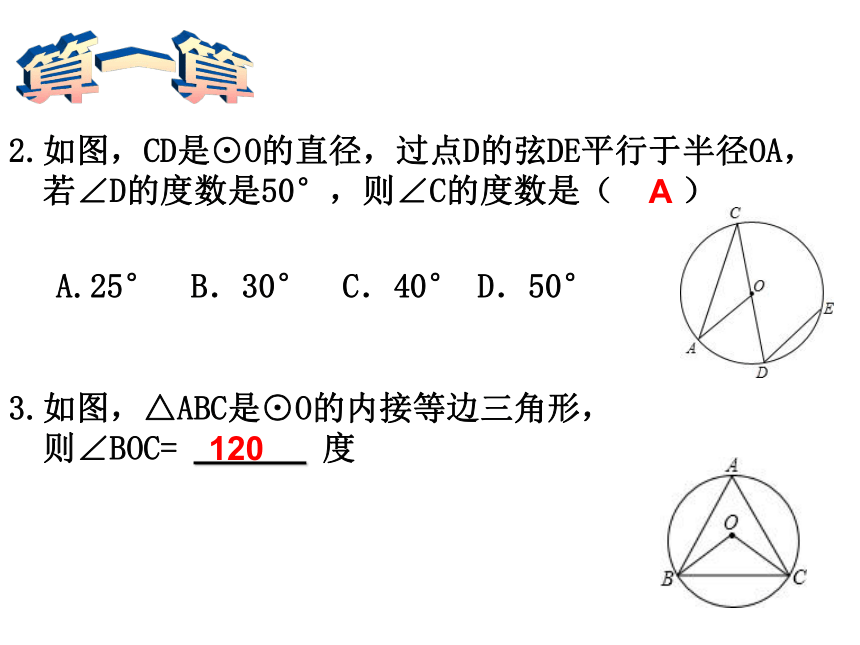
若∠D的度数是50°，则∠C的度数是（　　） A.25° B．30° C．40° D．50°算一算A1203.如图，△ABC是⊙O的内接等边三角形，
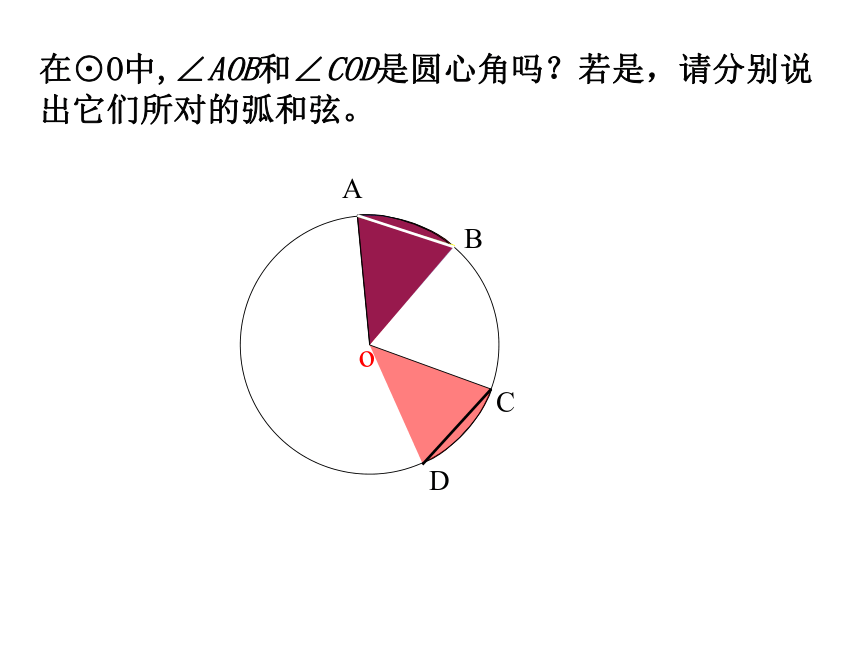
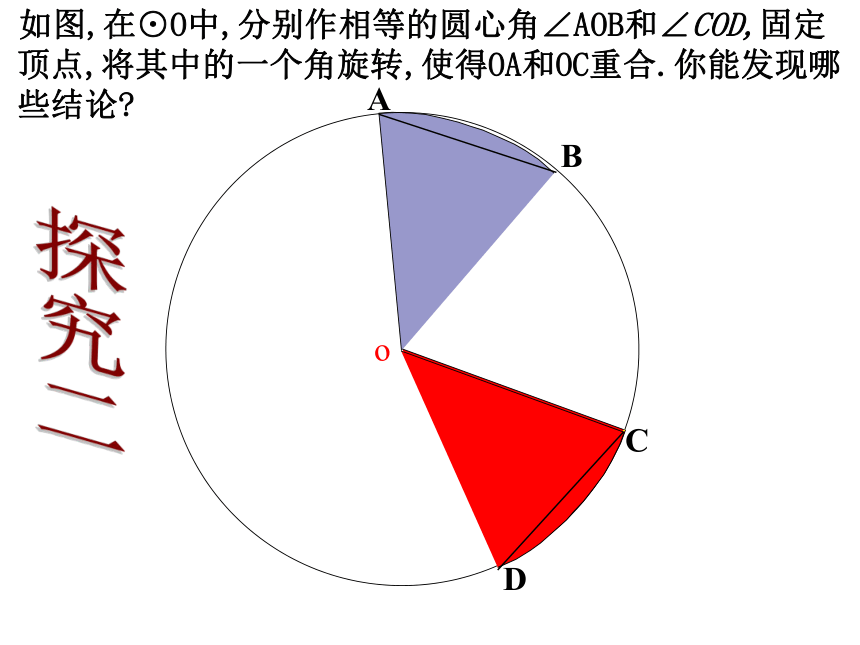
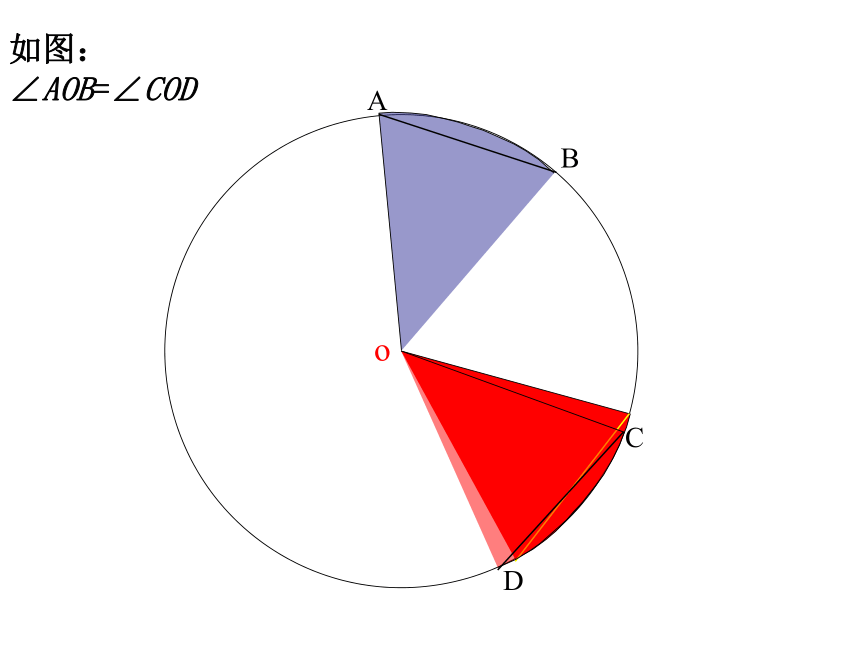
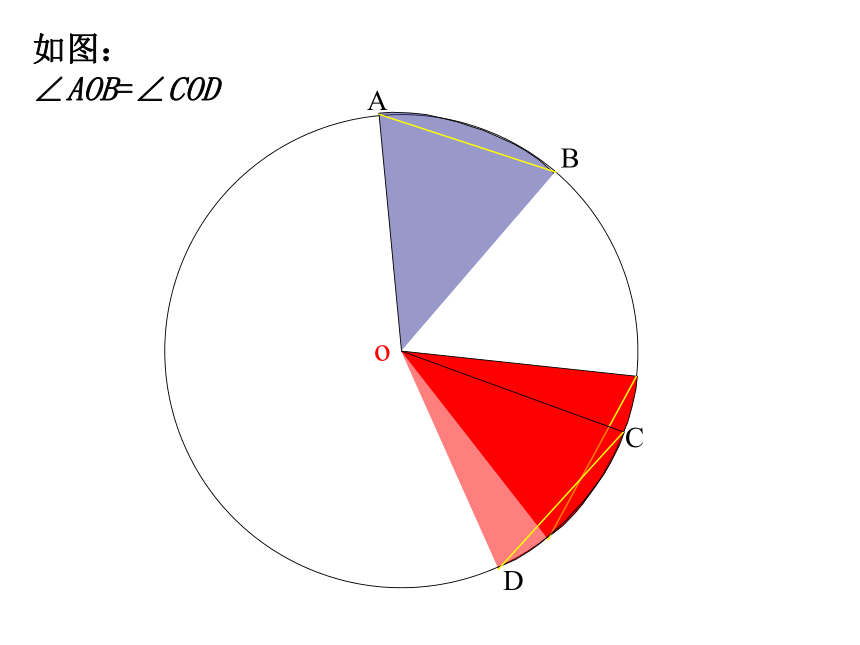
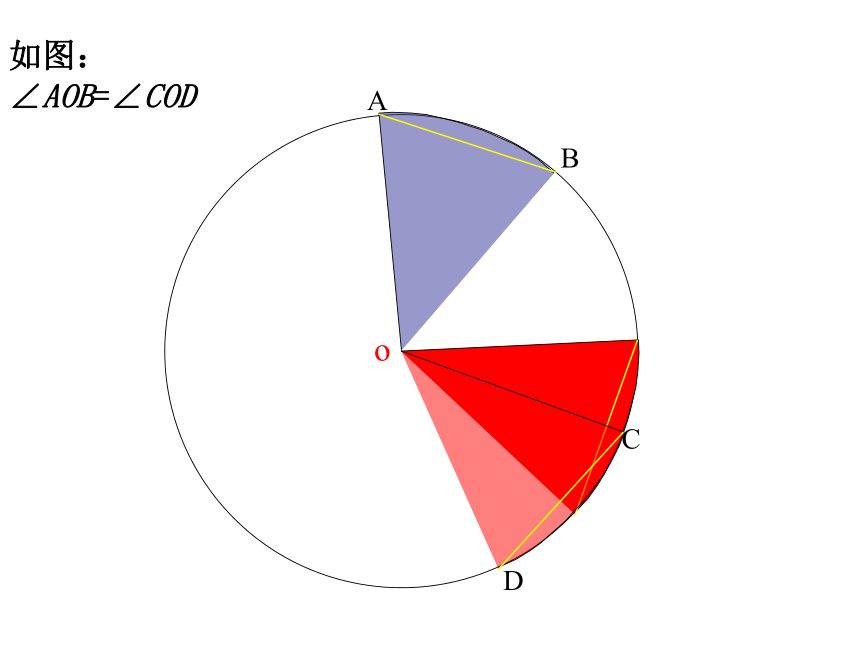
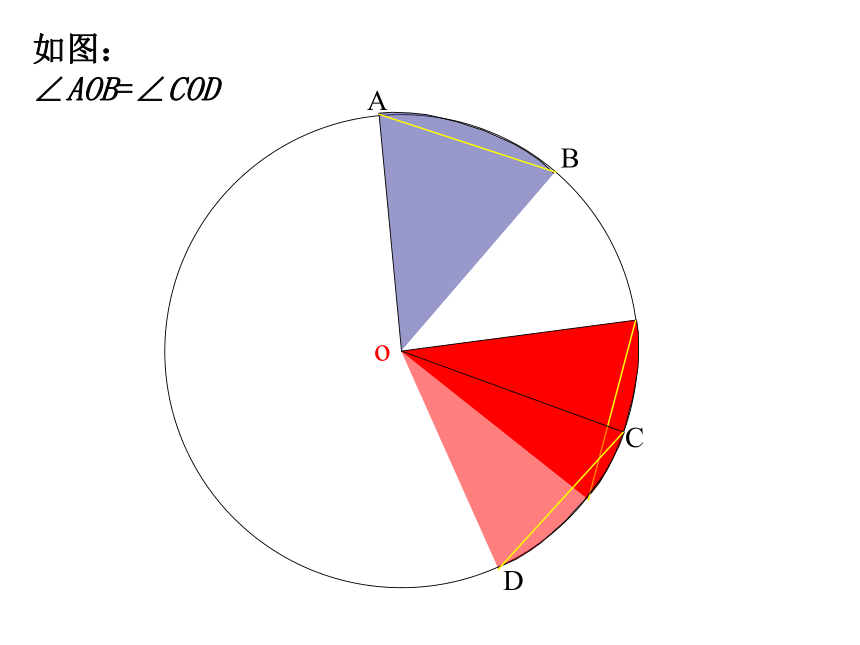
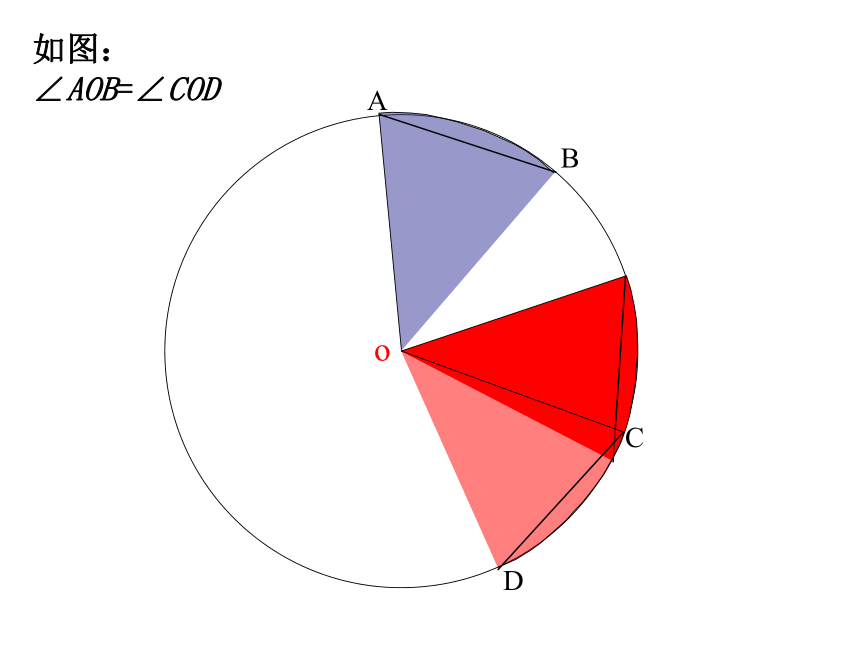
则∠BOC= _______ 度在⊙O中,∠AOB和∠COD是圆心角吗？若是，请分别说出它们所对的弧和弦。ABCDo探究二 如图,在⊙O中,分别作相等的圆心角∠AOB和∠COD,固定顶点,将其中的一个角旋转,使得OA和OC重合.你能发现哪些结论?ABCDo如图： ∠AOB=∠CODABCDo如图： ∠AOB=∠CODABCDo如图： ∠AOB=∠CODABCDo如图： ∠AOB=∠CODABCDo如图： ∠AOB=∠CODABCDo如图： ∠AOB=∠CODABCDo如图： ∠AOB=∠CODABCDo(C)(D)如图： ∠AOB=∠COD
∵OA=OC ，OB=OD，
∠AOB=∠COD,
∴当点A与点C重合时，
点B与点D也重合。
∴　AB=CD，
弦AB和弦CＤ对应的弦心距有什么关系？理由 如图,如果在两个等圆⊙O和⊙O′中,分别作相等的圆心角和∠AOB和∠A′O′B′,固定圆心,将其中的一个旋转一个角度,使得OA和O′A′重合.你又能发现哪些结论？明辨是非归纳结论圆心角定理 　　　　　　　　　　　在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对弦的
弦心距相等。　　　　　　　　条件结论在同圆或等圆中
圆心角相等圆心角所对的弧相等圆心角所对弦的弦心距相等圆心角所对的弦相等例题讲解例1、用直尺和圆规，你能完成以下圆的等分吗？（1）2等分；（2）4等分；（3）6等分；（4）3等分；挑战：只用圆规把一
个圆四等分1°圆心角所对的弧叫做1°的弧归纳结论 n°的圆心角所对的弧就是n°的弧．1.如图,在⊙Ｏ中,BC为⊙Ｏ的一条弦且等于⊙Ｏ的半径,
则弧BC的度数是 _______
600练一练２.如图,在⊙O中,AB为直径，∠BAC=400,则弧BC的
度数为____，弧AC的度数为____80010003.如图,两个同心圆的圆心为Ｏ,大圆半径OA,OB分别
交小圆于C,D两点，如果弧AB的度数是60°,那么弧
CD的度数_______ 60°.
等于4.如图,⊙Ｏ的直径AB垂直于弦CD,垂足为E，
∠COD＝100o，求弧BC,AD的度数求弧的度数时，往往先求出这段弧所对的圆心角的度数练一练例2.如图，在⊙O中，弦AB=CD.
????????????????????????????????例题讲解求证： AC=BD ???例题讲解例3.如图，CD为⊙O的直径，以点D为圆心，DO的长为
半径作弧，交⊙O于两点A，B.?
证明： ?????????????????????????????????. 变式训练1.如图，AB是⊙O的直径，OC⊥AB,点D是CO 的中点 ,
DE ∥AB，你能说明弧EC与弧EA的关系吗？变式训练2.如图，将⊙O沿着弦AB翻折，劣弧恰好经过圆心Ο，
若⊙O的半径为4，求弦AB的长度． 如图,A点是半圆上一个三等分点,B点是 的中点，P是
直径MN上一动点，⊙O的半径为1，求PA＋PB的最小值.拓展应用1.基本概念：圆心角的概念收获:2.基本性质：①圆的轴对称性、中心对称性、旋转不变性
②圆心角定理
③弧的度数和它所对圆心角的度数相等.3.基本方法：
①在运用圆心角定理时，首先要考虑定理的前提。
②在求一些弧的度数时，往往先考虑求出这段弧所对的 圆心角的度数
③在同圆或等圆中，要说明两段弧或两段弦相等时，往往先考虑求出这段弧所对的圆心角相等